1. INTRODUCTION
With the development of oceanology, more and more complex underwater missions are demanded in both military operations and civil applications, in which it is difficult for a single Unmanned Underwater Vessel (UUV) to satisfy the mission demands, thus pushing the development of Multiple UUVs (MUUVs) technology. One of the challenges in the MUUV field is precise localisation for long-range travel in an unknown environment.
The traditional method for the localisation of MUUVs in an unknown environment is inertial navigation (Grenon et al., Reference Grenon, An, Smith and Healey2005), however a high precision Inertial Navigation System (INS) is very expensive and its localisation error grows with time. To save cost and improve localisation accuracy, it is necessary to introduce a Master-Slave cooperative navigation framework in which structure the master UUV is equipped with an acoustic modem and high precision INS, and each slave UUV is equipped with an acoustic modem and low precision INS for Dead-Reckoning (DR). The Cooperative Localisation (CL) of MUUVs means that each slave UUV in the group receives Relative Localisation Information (RLI) from the master UUV by acoustic communication to improve their individual position estimations. According to the earlier work on this subject (Bahr et al., Reference Bahr, Leonard and Fallon2009a; Papadopoulos et al., Reference Papadopoulos, Fallon, Leonard and Patrikalakis2010), the RLI during cooperative navigation usually includes the master UUV location information and the relative range between UUVs.
CL techniques have been applied to indoor and outdoor robots (Nerurkar et al., Reference Nerurkar, Roumeliotis and Martinelli2009; Huang et al., Reference Huang, Trawny, Mourikis and Roumeliotis2011). Roumeliotis and Bekey (Reference Roumeliotis and Bekey2002) compared the advantages and disadvantages of the following three algorithms: individual DR, normal CL with continuous RLI exchange and master-slave CL with intermittent RLI exchange for localisation of three moving robots. A centralised Kalman filter estimator that can produce the uniform accuracy for every member of the robot group was introduced in Mourikis and Roumeliotis (Reference Mourikis and Roumeliotis2006).
Compared to mobile robots, there were fewer CL techniques for application in MUUVs until now. As shown in Fallon et al. (Reference Fallon, Papadopoulos, Leonard and Patrikalakis2010), communication delay is the hardest challenge for the CL of MUUVs because of the poor underwater environment. All types of preceding CL techniques for robots estimate the location at the present time based on a prior estimate and present relative measurement (Yang et al., Reference Yang, Freeman and Lynch2008). However, in the MUUV case, the relative measurements which were transmitted through the communication channels cannot arrive at the target vehicles on time, so the delayed measurements may cause a loss in estimation efficiency, even the divergence of the estimation from the true values (Capitan et al., Reference Capitan, Merino, Caballero and Ollero2009).
Baccou et al. (Reference Baccou, Jouvencel, Creuze and Rabaud2001) designed the observation equation of CL with communication delay by the acoustic round-trip time method; they supposed that the master UUV navigated with a good dead reckoning and it could surface for relocation by GPS measurement, and each UUV of the group could determine its own absolute position with RLI exchange. Bahr et al. (Reference Bahr, Walter and Leonard2009b) analysed the disadvantages of radio communication between UUVs and introduced the method to synchronize data transmission for CL with the use of Pulse Per Second (PPS) signal. The recent experiment on the development of a synchronous-clock acoustic localisation system that was suitable for the CL of MUUVs was reported in Walls and Eustice (Reference Walls and Eustice2011). A Delayed Extended Kalman Filter (DEKF), which is designed to deal with the CL problem with acoustic communication delay, is presented in Yao et al. (Reference Yao, Xu and Yan.2009).
In practice, the master UUV's RLI is sampled at each sampling time, and then routed through a multi-hop network to slave UUVs. As a consequence, the RLI arrives at the slave UUV with non-deterministic delay, and in this paper, we assume that there are no measurements lost in the acoustic communication channel because of multi-path propagation technology (Climent et al., Reference Climent, Capella, Meratnia and Serrano2012). Early work on the delay system has shown that the measurement delay could be reduced by network coding (Ahlswede et al., Reference Ahlswede, Cai, Li and Yeung2000), distributed signal processing (Ye et al., Reference Ye, Abouzeid and Ai2009), data compression (Twycross and Aickelin, Reference Twycross and Aickelin2010), and packet routing protocols (Akyildiz et al., Reference Akyildiz, Melodia and Chowdhury2007), but not completely avoided due to the inherently unreliable nature of acoustic communication. Previous research has focused on solving the communication delay problem with the use of the varied optimal state estimation methods. Schenato (Reference Schenato2008) has analysed the performance of estimators subject to random packet delay; he has designed the two alternative optimal estimators based on finite memory buffers and constant gains. At the end of the paper, he proved the necessary and sufficient conditions for the existence of stable estimators. Liang et al. (Reference Liang, Chen and Pan2010) proposed a Linear Minimum Variance (LMV) filter using the orthogonality principle to deal with the linear packet delay system with stochastic parameters. The method that uses the latest present measurements to replace the current data which did not arrive at the slave UUV site is discussed in Xue et al. (Reference Xue, Li and Zhu2012), in this algorithm, the arrival process of RLI is considered as an independent and Bernoulli distributed white sequence taking values of 0 and 1.
Moving horizon estimation (MHE) obtains a state estimation by using a moving, limited horizon of measurements. This reduces the sensitivity of the estimator to the effect of random delayed measurements (Liu et al., Reference Liu, Yu, Zhang and Chen2013). The basic strategy of MHE is to reformulate the estimation problem as a quadratic program, which is computed by minimizing a cost function that is a trade-off between process noise, measurement noise, and the estimate covariance of the states in the horizon. Early work on the application of MHE for linear systems was done by Farina et al. (Reference Farina, Trecate and Scattolini2010) and Kühl et al. (Reference Kühl, Diehl, Kraus, Schlöder and Bock2011). Rao et al. (Reference Rao, Rawlings and Mayne2003) analysed the relationship between the full information estimation and fixed size moving horizon approximation, and summarised the effect of the measurements that arrived before the sliding estimation window with the definition of the cost function. A MHE method for control systems with multiple packet delays in communication channels has been studied in Rao et al. (Reference Rao, Rawlings and Lee2001). This work reformulates the cost function with two nonnegative weight parameters to balance the effect of one-step state prediction at the beginning of the sliding horizon and the distances of the estimation measurements from the observations. What is more, most of the early studies assumed that the system noises have Gaussian distribution with mean zero. This has ignored the fact that the assumed properties of the Gaussian white noises are rarely met in practical CL operations, and that MHE can obtain the error between the real practical noise and the ideal Gaussian white noise with the state and measurement equations.
The formation and solution of the KKT system is the most expensive step in MHE algorithms. The strategies to solve the KKT system are shown in Zavala et al. (Reference Zavala, Laird and Biegler2007) and Huang et al. (Reference Huang, Biegler and Patwardhan2010). A popular strategy consisting of a forward Riccati decomposition that exploits the natural forward structure of the full KKT matrix is introduced in Zavala et al. (Reference Zavala, Laird and Biegler2008). In order to reduce the computation time during the reality application, we will exploit the band-diagonal structure of the KKT matrix and decomposition the matrix by “Lower Upper” (LU) factorization.
The remainder of the paper is organized as follows. Section 2 describes the problem formulation and the DEKF is also introduced. The MHE strategy proposed for the state estimation with time delay is introduced in Section 3 based on the decomposition of the KKT system by LU factorization that is realized by Riccati-based recursion. A test example is carried out to demonstrate the effectiveness of the proposed algorithms in Section 4. Then, in Section 5, the conclusion is given.
2. PROBLEM FORMULATION
The MUUV CL model without communication time delay is stated as a discrete time-varying dynamic process with stochastic characteristics as follows:
where k ∈ ℕ = {1, 2, ⋯}denotes the discrete sample time, X k ∈ ℝn, w k ∈ W ⊂ ℝu, Z k ∈ ℝm, v k ∈ V ⊂ ℝm are the state, process noise, measurement, measurement noise at time k, respectively, and Q k, R k are the covariance of w k, v k. Furthermore, the sets W, V are polyhedral and convex with 0 ∈ W, 0 ∈ V, and H k ∈ ℝm × n is the known time-varying matrix at time k.
The measurements from the sensors of the master UUV for CL are time-stamped, encapsulated into packets, and then transmitted to the slave UUV with random delay. In the initial period, the UUVs can get the global clock synchronization by Pulse Per Second (PPS) signal of GPS when they are on the surface. In case the RLI arrives out of order, time-stamping is necessary to reorder packets by global clock at the slave UUV site. Thus we can assume that all the sensor measurements delivered to the slave UUV are stored in a buffer in transmitting order. And the arrival process can be recognized via a random variable that just takes values of 0 and 1 as follows:
 $$\mu _k^t = \left\{ {\matrix{ 1 & {if\; measurement\; {Z_k}\; \; arrived\; at\; the} & {} \cr {} & {slaver\; UUV\; \; before\; or\; at\; time\; t} & {t \ge k} \cr 0 & {otherwise} & {} \cr}} \right.$$
$$\mu _k^t = \left\{ {\matrix{ 1 & {if\; measurement\; {Z_k}\; \; arrived\; at\; the} & {} \cr {} & {slaver\; UUV\; \; before\; or\; at\; time\; t} & {t \ge k} \cr 0 & {otherwise} & {} \cr}} \right.$$
From the definition, we can get that ![]() ${\rm \;} \forall h \in {\rm {\opf {N}}},{\rm \;} \; (\mu _k^t = 1) \Rightarrow (\mu _k^{t + k} = 1)$, which means that if the measurement Z k is present at time k, then it will be present for all future times. This paper studies the state estimation for CL of MUUVs in the scenario where there are no measurements lost in the acoustic communication channel with the use of multi-path propagation technology. So that communication delay Δk can be defined as follows:
${\rm \;} \forall h \in {\rm {\opf {N}}},{\rm \;} \; (\mu _k^t = 1) \Rightarrow (\mu _k^{t + k} = 1)$, which means that if the measurement Z k is present at time k, then it will be present for all future times. This paper studies the state estimation for CL of MUUVs in the scenario where there are no measurements lost in the acoustic communication channel with the use of multi-path propagation technology. So that communication delay Δk can be defined as follows:
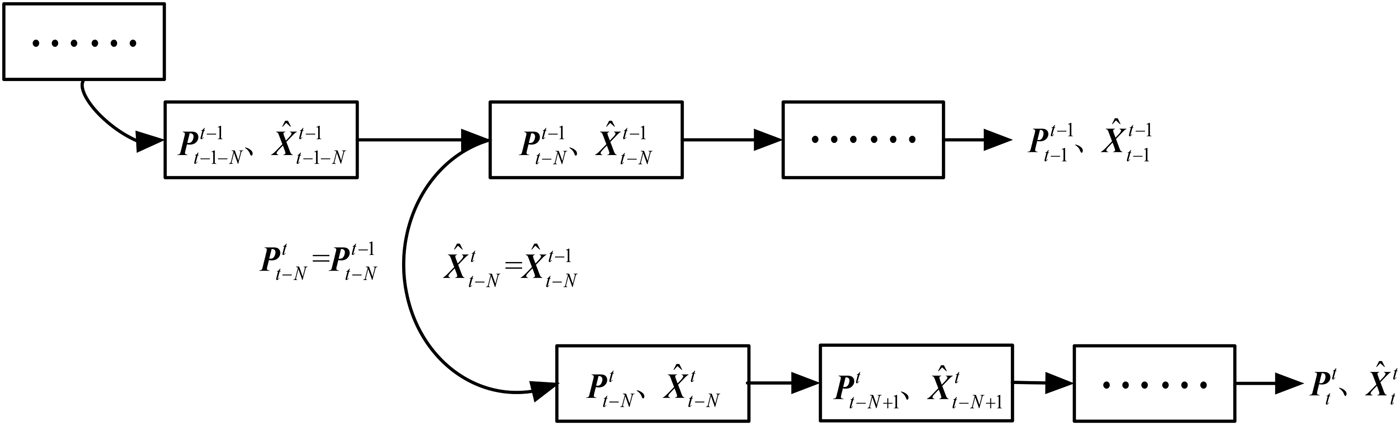
where γ k means at which time that Z k arrives at the slave UUV, since the communication delay is random, probably Z k is present and Z n (n < k, n ∈ ℕ) is not present at time t. Also it is possible that between two sampling times no RLI, or multiple measurements have arrived (see Figure 1). If we define a constant variable N ∈ ℕ+ as follows:

Figure 1. The arriving sequence and storage of the RLI at the slave UUV site, where N represents the maximum delay. Shaded blue squares represent the successfully arrived RLI at UUV. The cursor indicates current time.
Variable N means that the measurement Z k arrives at the slave UUV within N sample times of present time, and N is the biggest communication delay step. In this case, at time t (t ≥ N) we can use a buffer of limit length N to store measurements which are sent from time (t−N + 1) to time t (see Figure 1, t = N). Notice that at the beginning (N−1) sampling periods, some slots of the buffer stored nothing (see Figure 1, t = N−1).
If measurement Z k (k ∈ (t−N,t)) has not yet arrived at time t, we assume that a zero is stored in the k-slot of the buffer. So the value stored in the k-slot of the buffer at time t can be written as follows:
Then the MUUV CL model with communication delay at time t can be stated as follows:
where the observation matrix is ![]() ${\rm \;} C_k^t = \mu _k^t {H_k}$, and random variable
${\rm \;} C_k^t = \mu _k^t {H_k}$, and random variable ![]() $v_k^t = \; \mu _k^t {v_k}$ is uncorrelated, zero-mean white noise with covariance
$v_k^t = \; \mu _k^t {v_k}$ is uncorrelated, zero-mean white noise with covariance ![]() ${\rm \;} R_k^t = \; \mu _k^t {R_k}$. For any fixed t and N, the CL model can be seen as a linear time-varying system with respect to time step k. Our goal is to compute the optimal estimation
${\rm \;} R_k^t = \; \mu _k^t {R_k}$. For any fixed t and N, the CL model can be seen as a linear time-varying system with respect to time step k. Our goal is to compute the optimal estimation ![]() ${\hat {X}}_{t}^{t} \mathop{=}\limits^{\Delta} E [{X_t} \vert {\widetilde Z}_{k}^{t}, {X_0},{P_0}]$. With the normal time-varying Kalman method, it is necessary to compute
${\hat {X}}_{t}^{t} \mathop{=}\limits^{\Delta} E [{X_t} \vert {\widetilde Z}_{k}^{t}, {X_0},{P_0}]$. With the normal time-varying Kalman method, it is necessary to compute ![]() $\hat { X_t^t}$,
$\hat { X_t^t}$, ![]() $P_t^t $ starting from k = 1 to take advantage of the new measurements which arrived at present time step t as follows:
$P_t^t $ starting from k = 1 to take advantage of the new measurements which arrived at present time step t as follows:
 $$\eqalign{P_{{k + 1} \vert k}^t = {Q_k} + {A_k}P_{ k \vert k - 1}^t A_k^T - {A_k}P_{k \vert k - 1}^t \mu _k^t {H_k}^T \cr \times({H_k}P_{k \vert k - 1}^t {H_k}^T + {R_k})^{ - 1}{H_k}P_{k \vert k - 1}^t A_k^T }$$
$$\eqalign{P_{{k + 1} \vert k}^t = {Q_k} + {A_k}P_{ k \vert k - 1}^t A_k^T - {A_k}P_{k \vert k - 1}^t \mu _k^t {H_k}^T \cr \times({H_k}P_{k \vert k - 1}^t {H_k}^T + {R_k})^{ - 1}{H_k}P_{k \vert k - 1}^t A_k^T }$$
where 1≤ k ≤ t, considering the fact that ∀t ≥ N, ![]() $\mu _{t - N}^t = \; \mu _{t - N}^{t - 1} = 1$, so
$\mu _{t - N}^t = \; \mu _{t - N}^{t - 1} = 1$, so ![]() $\hat X_{t - N}^t = \hat X_{t - N}^{t - 1} $ and
$\hat X_{t - N}^t = \hat X_{t - N}^{t - 1} $ and ![]() $P_{t - N}^t = P_{t - N}^{t - 1} {\rm \;} $ hold under the same conditions. In this case,
$P_{t - N}^t = P_{t - N}^{t - 1} {\rm \;} $ hold under the same conditions. In this case, ![]() $\hat { X_t^t}$,
$\hat { X_t^t}$, ![]() ${P_t^t} $ can be computed iteratively starting from k = t−N (see Figure 2).
${P_t^t} $ can be computed iteratively starting from k = t−N (see Figure 2).

Figure 2. The iterative computation of DEKF for ![]() $\hat {X_t^t}$,
$\hat {X_t^t}$, ![]() ${P_t^t} $. It is not necessary to compute
${P_t^t} $. It is not necessary to compute ![]() $\hat X_t^t $,
$\hat X_t^t $, ![]() $P_t^t $ at every time step t starting from k = 1, since
$P_t^t $ at every time step t starting from k = 1, since ![]() $\hat X_{t - N}^{t - 1} \; $ and
$\hat X_{t - N}^{t - 1} \; $ and ![]() $P_{t - N}^{t - 1} $ computed at the previous time step t−1 can be used.
$P_{t - N}^{t - 1} $ computed at the previous time step t−1 can be used.
The optimal estimator ![]() $\hat X_t^t $ can be computed iteratively using a buffer of finite length N, where
$\hat X_t^t $ can be computed iteratively using a buffer of finite length N, where ![]() $\hat X_k^t $ is given by Equations (8) to (12) for t−N ≤ k ≤ t and
$\hat X_k^t $ is given by Equations (8) to (12) for t−N ≤ k ≤ t and![]() ${\rm \;} \hat X_{t - N}^t = \hat X_{t - N}^{t - 1} $, where
${\rm \;} \hat X_{t - N}^t = \hat X_{t - N}^{t - 1} $, where ![]() $\hat X_{t - N}^{t - 1} $ is computed at time step k = t−1. As shown in Liu et al. (Reference Liu, Yu, Zhang and Chen2013), methods based on Kalman filtering may become suboptimal or even unstable when dealing with the random delay. This motivated the development of moving horizon estimation (MHE) schemes that can guarantee the observer convergence and stability in the time delay system.
$\hat X_{t - N}^{t - 1} $ is computed at time step k = t−1. As shown in Liu et al. (Reference Liu, Yu, Zhang and Chen2013), methods based on Kalman filtering may become suboptimal or even unstable when dealing with the random delay. This motivated the development of moving horizon estimation (MHE) schemes that can guarantee the observer convergence and stability in the time delay system.
3. MOVING HORIZON ESTIMATION METHOD
Moving horizon estimation is based on the idea of getting a state estimate by using a moving, limited horizon of measurements. Recall from Section 2, we can denote the length of the horizon with the variable N, and all successfully received observations have a delay step less than N time steps. In this paper, the form of MHE is
 $$\matrix{ {min} \cr {\left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t, \left\{ {{w_k}} \right\}_{k = t - N + 1}^{t - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{k = t - N + 1}^t v{{_k^t} ^T}R{{_k^t} ^{ - 1}}v_k^t + \mathop \sum \limits_{k = t - N + 1}^{t - 1} w_k^T Q_k^{ - 1} {w_k} +} \cr {{{\left( {X_{t - N + 1}^t - \hat X_{t - N + 1}^t {\rm \;}} \right)}^T}P{{_{t - N + 1}^t} ^{ - 1}}\left( {X_{t - N + 1}^t - \hat X_{t - N + 1}^t} \right)} \cr}} \right)\;. $$
$$\matrix{ {min} \cr {\left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t, \left\{ {{w_k}} \right\}_{k = t - N + 1}^{t - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{k = t - N + 1}^t v{{_k^t} ^T}R{{_k^t} ^{ - 1}}v_k^t + \mathop \sum \limits_{k = t - N + 1}^{t - 1} w_k^T Q_k^{ - 1} {w_k} +} \cr {{{\left( {X_{t - N + 1}^t - \hat X_{t - N + 1}^t {\rm \;}} \right)}^T}P{{_{t - N + 1}^t} ^{ - 1}}\left( {X_{t - N + 1}^t - \hat X_{t - N + 1}^t} \right)} \cr}} \right)\;. $$
This cost function is subjected to Equation (6) and (7). Equation (6) describes the state propagation in discrete time and Equation (7) is the observation equation of the system. ![]() $\left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t $ are the states to be estimated in the moving horizon, the other unknown variables in the cost function are the variables that denote the process noise
$\left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t $ are the states to be estimated in the moving horizon, the other unknown variables in the cost function are the variables that denote the process noise![]() ${\rm \;} \left\{ {{w_k}} \right\}_{k = t - N + 1}^{t - 1} $. The noise at time instant k = t is not included in the cost function because the system state
${\rm \;} \left\{ {{w_k}} \right\}_{k = t - N + 1}^{t - 1} $. The noise at time instant k = t is not included in the cost function because the system state ![]() $X_t^t $ is unrelated to w t. The third term in the cost function is the arrival cost, which was used to summarise the effect of the measurements not included in the estimation window like
$X_t^t $ is unrelated to w t. The third term in the cost function is the arrival cost, which was used to summarise the effect of the measurements not included in the estimation window like![]() ${\rm \;} \left\{ {\widetilde Z_k^t {\rm \;}} \right\}_{k = 1}^{t - N} $, where
${\rm \;} \left\{ {\widetilde Z_k^t {\rm \;}} \right\}_{k = 1}^{t - N} $, where ![]() ${\rm \;} \hat X_{t - N + 1}^t $ is the DEKF state estimation at the beginning of the horizon, with covariance
${\rm \;} \hat X_{t - N + 1}^t $ is the DEKF state estimation at the beginning of the horizon, with covariance![]() ${\rm \;} P_{t - N + 1}^t $. The output of the MHE is
${\rm \;} P_{t - N + 1}^t $. The output of the MHE is ![]() ${\rm \;} \left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t $: the estimated state vector of the total horizon. In this paper, it is assumed that no inequality constraints are present. This leads to a weighted nonlinear-least-squares problem, in which the weights are the inverse of the covariance matrices.
${\rm \;} \left\{ {X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t $: the estimated state vector of the total horizon. In this paper, it is assumed that no inequality constraints are present. This leads to a weighted nonlinear-least-squares problem, in which the weights are the inverse of the covariance matrices.
If we define the state error as the difference between previous state estimation and the real state sequence ![]() ${\rm \;} \Delta X_k^t = X_k^t - \bar X_k^t $, and the process noise error as the difference between the real noise and the ideal Gaussian white noise
${\rm \;} \Delta X_k^t = X_k^t - \bar X_k^t $, and the process noise error as the difference between the real noise and the ideal Gaussian white noise ![]() $\; \Delta {w_k} = \; {w_k} - {\bar w_k}$, the MHE method can be reformulated by minimizing a cost function which is a trade-off between state error, process noise error and the estimate covariance of the states at the initial time instant of the horizon as follows
$\; \Delta {w_k} = \; {w_k} - {\bar w_k}$, the MHE method can be reformulated by minimizing a cost function which is a trade-off between state error, process noise error and the estimate covariance of the states at the initial time instant of the horizon as follows
 $$\matrix{ {min} \cr {\left\{ {\Delta X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t, \left\{ {\Delta {w_k}} \right\}_{k = t - N + 1}^{t - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{k = t - N + 1}^t \left\Vert {\tilde Z_k^t - h\left( {\bar X_k^t + \Delta X_k^t, {{\bar w}_k} + \; \Delta {w_k}} \right)} \right\Vert_{R{{_k^t} ^{ - 1}}}^2} \cr { + \mathop \sum \limits_{k = t - N + 1}^{t - 1} \left\Vert {{{\bar w}_k} + \Delta {w_k}} \right\Vert_{Q_k^{ - 1}} ^2} \cr { + \left\Vert {\bar X_{t - N + 1}^t + \Delta X_{t - N + 1}^t - \hat X_{t - N + 1}^t} \right\Vert{\rm} _{P{{_{t - N + 1}^t} ^{ - 1}}}^2} \cr}} \right)$$
$$\matrix{ {min} \cr {\left\{ {\Delta X_k^t {\rm \;}} \right\}_{k = t - N + 1}^t, \left\{ {\Delta {w_k}} \right\}_{k = t - N + 1}^{t - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{k = t - N + 1}^t \left\Vert {\tilde Z_k^t - h\left( {\bar X_k^t + \Delta X_k^t, {{\bar w}_k} + \; \Delta {w_k}} \right)} \right\Vert_{R{{_k^t} ^{ - 1}}}^2} \cr { + \mathop \sum \limits_{k = t - N + 1}^{t - 1} \left\Vert {{{\bar w}_k} + \Delta {w_k}} \right\Vert_{Q_k^{ - 1}} ^2} \cr { + \left\Vert {\bar X_{t - N + 1}^t + \Delta X_{t - N + 1}^t - \hat X_{t - N + 1}^t} \right\Vert{\rm} _{P{{_{t - N + 1}^t} ^{ - 1}}}^2} \cr}} \right)$$
For notational convenience we will from now on rename the state and measurement function as![]() ${\rm \;} f\left( {\bar X_k^t, {{\bar w}_k}} \right) = f_k^t $,
${\rm \;} f\left( {\bar X_k^t, {{\bar w}_k}} \right) = f_k^t $,![]() $\; h\left( {\bar X_k^t, {{\bar w}_k}} \right) = h_{k} ^t $, we obtain the first order Taylor expansions of state and observation equations as:
$\; h\left( {\bar X_k^t, {{\bar w}_k}} \right) = h_{k} ^t $, we obtain the first order Taylor expansions of state and observation equations as:
where A k, G k, B k, J k are the parameter matrices of state and observation equations, respectively. In each recursion, the state propagation functions ![]() ${\rm \;} f_k^t \; $ and the measurement function
${\rm \;} f_k^t \; $ and the measurement function ![]() $h_k^t $ are linearized near the previous state estimation
$h_k^t $ are linearized near the previous state estimation ![]() ${\rm \;} \bar X_k^t $ and the ideal Gaussian process noise
${\rm \;} \bar X_k^t $ and the ideal Gaussian process noise ![]() $\; {\bar w_k}$. For convenience, in the remainder of this paper, the time indices are redefined so that the measurement horizon always starts with index 1 and ends with index N without loss of generality. Time index 1 denotes the beginning of the horizon at time t−N + 1, and time index N always denotes the current time t. The MHE problem is here stated as follows:
$\; {\bar w_k}$. For convenience, in the remainder of this paper, the time indices are redefined so that the measurement horizon always starts with index 1 and ends with index N without loss of generality. Time index 1 denotes the beginning of the horizon at time t−N + 1, and time index N always denotes the current time t. The MHE problem is here stated as follows:
 $$\matrix{ {min} \cr {\left\{ {\Delta X_j^N {\rm \;}} \right\}_{\,j = 1}^N, \left\{ {\Delta {w_j}} \right\}_{\,j = 1}^{N - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{\,j = 1}^{N - 1} \left\Vert {\tilde Z_j^N - h_j^N - {B_j}\Delta X_j^N - {J_j}\Delta {w_j}} \right\Vert_{R{{_j^N} ^{ - 1}}}^2} \cr { + \left\Vert {\tilde Z_N^N - H_N^N \bar X_N^N - H_N^N \Delta X_N^N} \right\Vert _{R{{_N^N} ^{ - 1}}}^2} \cr { + \mathop \sum \limits_{\,j = 1}^{N - 1} \left\Vert {{{\bar w}_j} + \Delta {w_j}} \right\Vert_{Q_j^{ - 1}} ^2 + \left\Vert {\bar X_1^N + \Delta X_1^N - \hat X_1^N} \right\Vert _{P{{_1^N} ^{ - 1}}}^2} \cr}} \right)$$
$$\matrix{ {min} \cr {\left\{ {\Delta X_j^N {\rm \;}} \right\}_{\,j = 1}^N, \left\{ {\Delta {w_j}} \right\}_{\,j = 1}^{N - 1}} \cr} \left( {\matrix{ {\mathop \sum \limits_{\,j = 1}^{N - 1} \left\Vert {\tilde Z_j^N - h_j^N - {B_j}\Delta X_j^N - {J_j}\Delta {w_j}} \right\Vert_{R{{_j^N} ^{ - 1}}}^2} \cr { + \left\Vert {\tilde Z_N^N - H_N^N \bar X_N^N - H_N^N \Delta X_N^N} \right\Vert _{R{{_N^N} ^{ - 1}}}^2} \cr { + \mathop \sum \limits_{\,j = 1}^{N - 1} \left\Vert {{{\bar w}_j} + \Delta {w_j}} \right\Vert_{Q_j^{ - 1}} ^2 + \left\Vert {\bar X_1^N + \Delta X_1^N - \hat X_1^N} \right\Vert _{P{{_1^N} ^{ - 1}}}^2} \cr}} \right)$$Subject to
If we define the unknown variable vector as ![]() $y =(\Delta X{_1^{N ^T}}\!\!,{\rm \Delta} w_1^T, \cdots \cdots \Delta X{_{N - 1}^{N ^{\;\;\;\;\;\;T}}},\rm \Delta w_{N - 1}^T, \Delta X{_N^{N ^T})^T}$, the MHE problem described in Equation (19) can be transformed into a Quadratic programming (QP) problem as:
$y =(\Delta X{_1^{N ^T}}\!\!,{\rm \Delta} w_1^T, \cdots \cdots \Delta X{_{N - 1}^{N ^{\;\;\;\;\;\;T}}},\rm \Delta w_{N - 1}^T, \Delta X{_N^{N ^T})^T}$, the MHE problem described in Equation (19) can be transformed into a Quadratic programming (QP) problem as:
 $$\eqalign {& \quad \matrix{ min \cr y }\left({1 \over 2}{y^T}Gy + {g^T}y \right)\cr & \quad {\rm such \ that} \; \; \; \; \; {\it \Gamma} ^T y = {\it \Upsilon}}$$
$$\eqalign {& \quad \matrix{ min \cr y }\left({1 \over 2}{y^T}Gy + {g^T}y \right)\cr & \quad {\rm such \ that} \; \; \; \; \; {\it \Gamma} ^T y = {\it \Upsilon}}$$where G is a positive symmetric matrix, then Equation (21) is a strict convex QP and has a unique global solution. According to the KKT condition presented in Sun and Yuan (Reference Sun and Yuan2006), a vector of Lagrange multipliers is introduced for solving the equality-constrained QP problem as:
 $$\eqalign { & \nabla f\left( y^{\ast} \right) = \lambda \cdot \nabla c\left(y^{\ast} \right) \cr & \quad \quad \quad {\it \Gamma} ^{T}y = {\it \Upsilon} }$$
$$\eqalign { & \nabla f\left( y^{\ast} \right) = \lambda \cdot \nabla c\left(y^{\ast} \right) \cr & \quad \quad \quad {\it \Gamma} ^{T}y = {\it \Upsilon} }$$
where y* is the global minimizer, λ is the Lagrange multiplier, ![]() $f\left( y \right) = \displaystyle{1 \over 2}{y^T}Gy + {g^T}y, c(y)$ = Υ−Γ Ty, ∇ means the gradient of functions. With the expression of ∇f(y *), ∇c(y *), the KKT system in Equation (22) can be written in the matrix form:
$f\left( y \right) = \displaystyle{1 \over 2}{y^T}Gy + {g^T}y, c(y)$ = Υ−Γ Ty, ∇ means the gradient of functions. With the expression of ∇f(y *), ∇c(y *), the KKT system in Equation (22) can be written in the matrix form:
Let us rewrite the matrix equation as M ξ = r for short, and in order to get the sparse band structure of M matrix, we reorder the unknown variable vector of KKT system as follows:
 $$\eqalign{& {\left[ {{y^T}\!\!,{\lambda ^T}} \right]^T} = {\left[ {{\rm \Delta} \tau_1^T\!\!\!, \cdots \cdots, {\rm \Delta} \tau _{N - 1}^T, {\rm \Delta} X{{_N^N} ^T},\bar \lambda _1^T, \cdots \cdots, \bar \lambda _{N - 1}^T} \right]^T} {\bf \rightarrow} \cr & \quad \xi = {\left[ {{\rm \Delta} \tau _1^T, \bar \lambda _1^T, {\rm \Delta} \tau _2^T, \bar \lambda _2^T, \cdots \cdots {\rm \Delta} \tau _{N - 1}^T, \bar \lambda _{N - 1}^T, {\rm \Delta} X{{_N^N} ^T}} \right]^T}}$$
$$\eqalign{& {\left[ {{y^T}\!\!,{\lambda ^T}} \right]^T} = {\left[ {{\rm \Delta} \tau_1^T\!\!\!, \cdots \cdots, {\rm \Delta} \tau _{N - 1}^T, {\rm \Delta} X{{_N^N} ^T},\bar \lambda _1^T, \cdots \cdots, \bar \lambda _{N - 1}^T} \right]^T} {\bf \rightarrow} \cr & \quad \xi = {\left[ {{\rm \Delta} \tau _1^T, \bar \lambda _1^T, {\rm \Delta} \tau _2^T, \bar \lambda _2^T, \cdots \cdots {\rm \Delta} \tau _{N - 1}^T, \bar \lambda _{N - 1}^T, {\rm \Delta} X{{_N^N} ^T}} \right]^T}}$$
where ![]() ${\rm \; \Delta} {\tau _j} = \left( {{\rm \Delta} X{{_j^N} ^T}\!\!, {\rm \Delta} {w_j}^T} \right),{\bar \lambda _j} = {\lambda _j} \cdot {e_n}$,
${\rm \; \Delta} {\tau _j} = \left( {{\rm \Delta} X{{_j^N} ^T}\!\!, {\rm \Delta} {w_j}^T} \right),{\bar \lambda _j} = {\lambda _j} \cdot {e_n}$, ![]() $\lambda = {({\lambda _1},{\rm \;} \cdots \cdots, {\lambda _{N - 1}},{\lambda _N})^T}\; $ is the vector of Lagrange multipliers, e n = (1, ⋯⋯, 1)T with 2N dimensions. The KKT matrix and residual vector are defined as:
$\lambda = {({\lambda _1},{\rm \;} \cdots \cdots, {\lambda _{N - 1}},{\lambda _N})^T}\; $ is the vector of Lagrange multipliers, e n = (1, ⋯⋯, 1)T with 2N dimensions. The KKT matrix and residual vector are defined as:
 $$M = {\left[ {\matrix{ {{T_1}} & { - U_1^T} & 0 & {} & {} & {} & {} & {} \cr { - {U_1}} & 0 & E & {} & {} & {} & {} & {} \cr 0 & {{E^T}} & {{T_2}} & { - U_2^T} & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {{T_{N - 1}}} & { - U_{N - 1}^T} & 0 \cr {} & {} & {} & {} & {} & { - {U_{N - 1}}} & 0 & {{I_{n \times n}}} \cr {} & {} & {} & {} & {} & 0 & {I_{n \times n}^T} & {{T_N}} \cr}} \right]_,}\,r = \left[ {\matrix{ {{r_{{\tau _1}}}} \cr {{r_{{\lambda _1}}}} \cr {{r_{{\tau _2}}}} \cr \vdots \cr {{r_{{\tau _{N - 1}}}}} \cr {{r_{{\lambda _{N - 1}}}}} \cr {{r_{{\tau _N}}}} \cr}} \right]$$
$$M = {\left[ {\matrix{ {{T_1}} & { - U_1^T} & 0 & {} & {} & {} & {} & {} \cr { - {U_1}} & 0 & E & {} & {} & {} & {} & {} \cr 0 & {{E^T}} & {{T_2}} & { - U_2^T} & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {{T_{N - 1}}} & { - U_{N - 1}^T} & 0 \cr {} & {} & {} & {} & {} & { - {U_{N - 1}}} & 0 & {{I_{n \times n}}} \cr {} & {} & {} & {} & {} & 0 & {I_{n \times n}^T} & {{T_N}} \cr}} \right]_,}\,r = \left[ {\matrix{ {{r_{{\tau _1}}}} \cr {{r_{{\lambda _1}}}} \cr {{r_{{\tau _2}}}} \cr \vdots \cr {{r_{{\tau _{N - 1}}}}} \cr {{r_{{\lambda _{N - 1}}}}} \cr {{r_{{\tau _N}}}} \cr}} \right]$$
where ![]() ${r_{{\tau _j}}}{\rm \;} $ denotes the dual residual associated with
${r_{{\tau _j}}}{\rm \;} $ denotes the dual residual associated with ![]() ${\rm \; \Delta} {\tau _j}$,
${\rm \; \Delta} {\tau _j}$, ![]() ${r_{{\lambda _j}}}{\rm \;} $ denotes the primal residual associated with
${r_{{\lambda _j}}}{\rm \;} $ denotes the primal residual associated with ![]() ${\bar \lambda _j}$, and we define:
${\bar \lambda _j}$, and we define:
 $$\eqalignno{ {T_1} &= \left[ {\matrix{ {2\left( {B_1^T R_1^{ - 1} {B_1} + P{{_1^N} ^{ - 1}}} \right)} & { - 2B_1^T {J_1}} \cr { - 2J_1^T {B_1}} & {2\left( {J_1^T R_1^{ - 1} {J_1} + Q_1^{ - 1}} \right)} \cr}} \right]\!,\cr{r_{{\tau _1}}} &= \left[ {\matrix{ {B_1^T R_1^{ - 1} \left( {\tilde Z_1^N - h_1^N} \right) - P{{_1^N} ^{ - 1}}\left( {\bar X_1^N - \hat X_1^N} \right)} \cr {J_1^T R_1^{ - 1} \left( {\tilde Z_1^N - f_1^N} \right) - Q_1^{ - 1} {{\bar w}_1}} \cr}} \right] \cr & {T_j} = \left[ {\matrix{ {2B_j^T R_j^{ - 1} {B_j}} & { - 2B_j^T {J_j}} \cr { - 2J_j^T {B_j}} & {2\left( {J_j^T R_j^{ - 1} {J_j} + Q_j^{ - 1}} \right)} \cr}} \right]\!,\quad{r_{{\tau _j}}} = \left[ {\matrix{ {B_j^T R_j^{ - 1} \left( {\tilde Z_j^N - h_j^N} \right)} \cr {J_j^T R_j^{ - 1} \left( {\tilde Z_j^N - h_j^N} \right) - Q_j^{ - 1} {{\bar w}_j}} \cr}} \right] \cr & {T_N} = \left[ {2H_N^T R_N^{ - 1} {H_N}} \right]\!,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{r_{{\tau _N}}} = \left[ {H_N^T R_N^{ - 1} \left( {\tilde Z_N^N - {H_N}\bar X_N^N} \right)} \right] \cr & {U_k} = \left[ {\matrix{ {{A_k}} & {{G_k}} \cr}} \right]\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,E = \left[ {\matrix{ {{I_{n \,\times\, n}}} & {{0_{n \,\times\, n}}} \cr}} \right]\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm \;} {r_{{\lambda _j}}} = \left[ {\,f_j^N - \bar X_j^N} \right].&(26)}$$
$$\eqalignno{ {T_1} &= \left[ {\matrix{ {2\left( {B_1^T R_1^{ - 1} {B_1} + P{{_1^N} ^{ - 1}}} \right)} & { - 2B_1^T {J_1}} \cr { - 2J_1^T {B_1}} & {2\left( {J_1^T R_1^{ - 1} {J_1} + Q_1^{ - 1}} \right)} \cr}} \right]\!,\cr{r_{{\tau _1}}} &= \left[ {\matrix{ {B_1^T R_1^{ - 1} \left( {\tilde Z_1^N - h_1^N} \right) - P{{_1^N} ^{ - 1}}\left( {\bar X_1^N - \hat X_1^N} \right)} \cr {J_1^T R_1^{ - 1} \left( {\tilde Z_1^N - f_1^N} \right) - Q_1^{ - 1} {{\bar w}_1}} \cr}} \right] \cr & {T_j} = \left[ {\matrix{ {2B_j^T R_j^{ - 1} {B_j}} & { - 2B_j^T {J_j}} \cr { - 2J_j^T {B_j}} & {2\left( {J_j^T R_j^{ - 1} {J_j} + Q_j^{ - 1}} \right)} \cr}} \right]\!,\quad{r_{{\tau _j}}} = \left[ {\matrix{ {B_j^T R_j^{ - 1} \left( {\tilde Z_j^N - h_j^N} \right)} \cr {J_j^T R_j^{ - 1} \left( {\tilde Z_j^N - h_j^N} \right) - Q_j^{ - 1} {{\bar w}_j}} \cr}} \right] \cr & {T_N} = \left[ {2H_N^T R_N^{ - 1} {H_N}} \right]\!,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{r_{{\tau _N}}} = \left[ {H_N^T R_N^{ - 1} \left( {\tilde Z_N^N - {H_N}\bar X_N^N} \right)} \right] \cr & {U_k} = \left[ {\matrix{ {{A_k}} & {{G_k}} \cr}} \right]\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,E = \left[ {\matrix{ {{I_{n \,\times\, n}}} & {{0_{n \,\times\, n}}} \cr}} \right]\,,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\rm \;} {r_{{\lambda _j}}} = \left[ {\,f_j^N - \bar X_j^N} \right].&(26)}$$In order to reduce the computation time of solving the KKT system, with the further exploitation of sparse band structure in the KKT matrix M, we decompose the KKT matrix by LU factorization, and then use the direct forward-backward Riccati recursion algorithm to solve the KKT system based on the structure of L and U matrix. We define L and U as:
 $$\eqalign{& L = \left[ \matrix{ {\prod\nolimits_1 {}} & 0 & 0 & {} & {} & {} & {} & {} \cr { - {U_1}} & {{S_1}} & 0 & {} & {} & {} & {} & {} \cr 0 & {{E^T}} & {\prod\nolimits_2 {}} & 0 & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {\prod\nolimits_{N - 1} {}} & 0 & 0 \cr {} & {} & {} & {} & {} & { - {U_{N - 1}}} & {{S_{N - 1}}} & 0 \cr {} & {} & {} & {} & {} & 0 & {I_{n \,\times\, n}^T} & {\prod\nolimits_N {}} \cr} \right], \cr & U = \left[ \matrix{ {{I_{2n \,\times\, 2n}}} & { -\!\! \prod\nolimits_1^{ - 1} {U_1^T}} & 0 & 0 & {} & {} & {} & {} \cr 0 & {{I_{n \,\times\, n}}} & {S_1^{ - 1} E} & 0 & {} & {} & {} & {} \cr 0 & 0 & {{I_{2n \,\times \,2n}}} & { - \!\prod\nolimits_2^{ - 1} {U_2^T}} & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {{I_{2n \,\times\, 2n}}} & { - \prod\nolimits_{N - 1}^{ - 1} {U_{N - 1}^T}} & 0 \cr {} & {} & {} & {} & {} & {} & {{I_{n \,\times\, n}}} & {S_{N - 1}^{ - 1} {I_{n \,\times\, n}}} \cr {} & {} & {} & {} & {} & {} & {} & {{I_{n \,\times\, n}}} \cr} \right]} $$
$$\eqalign{& L = \left[ \matrix{ {\prod\nolimits_1 {}} & 0 & 0 & {} & {} & {} & {} & {} \cr { - {U_1}} & {{S_1}} & 0 & {} & {} & {} & {} & {} \cr 0 & {{E^T}} & {\prod\nolimits_2 {}} & 0 & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {\prod\nolimits_{N - 1} {}} & 0 & 0 \cr {} & {} & {} & {} & {} & { - {U_{N - 1}}} & {{S_{N - 1}}} & 0 \cr {} & {} & {} & {} & {} & 0 & {I_{n \,\times\, n}^T} & {\prod\nolimits_N {}} \cr} \right], \cr & U = \left[ \matrix{ {{I_{2n \,\times\, 2n}}} & { -\!\! \prod\nolimits_1^{ - 1} {U_1^T}} & 0 & 0 & {} & {} & {} & {} \cr 0 & {{I_{n \,\times\, n}}} & {S_1^{ - 1} E} & 0 & {} & {} & {} & {} \cr 0 & 0 & {{I_{2n \,\times \,2n}}} & { - \!\prod\nolimits_2^{ - 1} {U_2^T}} & {} & {} & {} & {} \cr {} & {} & {} & {} & \ddots & {} & {} & {} \cr {} & {} & {} & {} & {} & {{I_{2n \,\times\, 2n}}} & { - \prod\nolimits_{N - 1}^{ - 1} {U_{N - 1}^T}} & 0 \cr {} & {} & {} & {} & {} & {} & {{I_{n \,\times\, n}}} & {S_{N - 1}^{ - 1} {I_{n \,\times\, n}}} \cr {} & {} & {} & {} & {} & {} & {} & {{I_{n \,\times\, n}}} \cr} \right]} $$To solve the KKT system, the matrices L and U do not need to be constructed. Instead the factors Πj, Sj are computed and directly applied to the residual vector. The solution vector ξ of primal and dual variables can be obtained after a forward solve Lξ′ = r followed by a backward solve Uξ = ξ′. The real-time computation algorithm is presented as Algorithm 1.
Algorithm 1: Real-time iteration of MHE
0, Input: the previous state estimation over the entire estimation horizon![]() ${\rm \;} \left\{ {\bar X_j^N {\rm \;}} \right\}_{j = 1}^N $,
${\rm \;} \left\{ {\bar X_j^N {\rm \;}} \right\}_{j = 1}^N $,
the parameter matrices of state and observation equations A k, G k, B k, J k. DEKF state estimation at the beginning of the horizon ![]() $\hat X_1^N $, and covariance
$\hat X_1^N $, and covariance![]() ${\rm \;} P_{t - N + 1}^t $. Update the arrive cost function as:
${\rm \;} P_{t - N + 1}^t $. Update the arrive cost function as: ![]() ${\bi arrive\; cost} = {\left( {X_1^N - \hat X_1^N {\rm \;}} \right)^T}P{_1^{N ^ - 1}}\left( {X_1^N - \hat X_1^N} \right)$.
${\bi arrive\; cost} = {\left( {X_1^N - \hat X_1^N {\rm \;}} \right)^T}P{_1^{N ^ - 1}}\left( {X_1^N - \hat X_1^N} \right)$.
1, Forward Riccati recursion solves Lξ′ = r with the factors Πj,Sj in matrices L and U at the beginning of the moving horizon:
 $${{\it \Pi} _1} = {T_1} = \left[ {\matrix{ {2\left( {B_1^T R_1^{ - 1} {B_1} + P{{_1^N} ^{ - 1}}} \right)} & { - 2B_1^T {J_1}} \cr { - 2J_1^T {B_1}} & {2\left( {J_1^T R_1^{ - 1} {J_1} + Q_1^{ - 1}} \right)} \cr}} \right]$$
$${{\it \Pi} _1} = {T_1} = \left[ {\matrix{ {2\left( {B_1^T R_1^{ - 1} {B_1} + P{{_1^N} ^{ - 1}}} \right)} & { - 2B_1^T {J_1}} \cr { - 2J_1^T {B_1}} & {2\left( {J_1^T R_1^{ - 1} {J_1} + Q_1^{ - 1}} \right)} \cr}} \right]$$FORj = 2 to N−1 DO
Update the matrices as 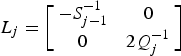 ${L_j} = \left[ {\matrix{ { - S_{j - 1}^{ - 1}} & 0 \cr 0 & {2Q_j^{ - 1}} \cr}} \right]$,
${L_j} = \left[ {\matrix{ { - S_{j - 1}^{ - 1}} & 0 \cr 0 & {2Q_j^{ - 1}} \cr}} \right]$, ![]() ${D_j} = \left[ {\matrix{ {{B_j}} & 0 \cr 0 & {{J_j}} \cr}} \right]$
${D_j} = \left[ {\matrix{ {{B_j}} & 0 \cr 0 & {{J_j}} \cr}} \right]$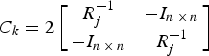 $ {C_k} = 2\left[ {\matrix{ {R_j^{ - 1}} & { - {I_{n \,\times\, n}}} \cr { - {I_{n \,\times\, n}}} & {R_j^{ - 1}} \cr}} \right]$
$ {C_k} = 2\left[ {\matrix{ {R_j^{ - 1}} & { - {I_{n \,\times\, n}}} \cr { - {I_{n \,\times\, n}}} & {R_j^{ - 1}} \cr}} \right]$
And then compute the factors Π j,Sj as:
Solve the equation Lξ′ = r as:
end;
the final time step: ![]() ${{\it \Pi} _N} = {T_N} - S_{N - 1}^{ - 1} $,
${{\it \Pi} _N} = {T_N} - S_{N - 1}^{ - 1} $, ![]() $\Delta X{^ \prime}_N^N = {\it \Pi} _{N - 1}^{ - 1} \left( {{r_{{\tau _N}}} - {{\overline {\lambda {^ \prime}}} _{N - 1}}} \right)$;
$\Delta X{^ \prime}_N^N = {\it \Pi} _{N - 1}^{ - 1} \left( {{r_{{\tau _N}}} - {{\overline {\lambda {^ \prime}}} _{N - 1}}} \right)$;
2, Backward Riccati recursion solves Uξ = ξ′ with the factors Πi j,Sj and ![]() ${\rm \Delta} \tau {{^ \prime}_j},{\overline {\lambda {^ \prime}} _j}$:
${\rm \Delta} \tau {{^ \prime}_j},{\overline {\lambda {^ \prime}} _j}$:
The first time step: ![]() $\Delta X_N^N = \Delta X{^ \prime}_N^N $
$\Delta X_N^N = \Delta X{^ \prime}_N^N $
FORj = N to 1 DO
End;
3, obtain the state estimation of the horizon: ![]() $X_j^N = \Delta X_j^N + \bar X_j^N \!$, and the real process noise is
$X_j^N = \Delta X_j^N + \bar X_j^N \!$, and the real process noise is![]() ${\rm \;} {w_j} = \; \Delta {w_j} + {\bar w_j}$, then involve this state estimation and noise in
${\rm \;} {w_j} = \; \Delta {w_j} + {\bar w_j}$, then involve this state estimation and noise in 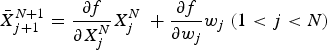 $\bar X_{j + 1}^{N + 1} = \displaystyle{{\partial f} \over {\partial X_j^N}} X_j^N \; + \displaystyle{{\partial f} \over {\partial {w_j}}}{w_j}\; (1 \lt j \lt N)$ to obtain the state estimation of the new horizon
$\bar X_{j + 1}^{N + 1} = \displaystyle{{\partial f} \over {\partial X_j^N}} X_j^N \; + \displaystyle{{\partial f} \over {\partial {w_j}}}{w_j}\; (1 \lt j \lt N)$ to obtain the state estimation of the new horizon![]() $\; \left\{ {\bar X_j^{N + 1} {\rm \;}} \right\}_{j = 2}^{N + 1} $.
$\; \left\{ {\bar X_j^{N + 1} {\rm \;}} \right\}_{j = 2}^{N + 1} $.
4. COOPERATION LOCALISATION OF MUUVS
In the localisation system, the master UUV is equipped with a high precision INS to obtain its own accurate location, and employs a WHOI micro-modem to yield a One-Way Travel Time (OWTT) range measurement between itself and the slave UUV as detailed in Freitag et al. (Reference Freitag, Grund, Singh, Partan, Koski and Ball2005). The location information of the master UUV and the relative range makes up of the master UUV's RLI. At each sample time, the RLI is transmitted to the slave UUVs through an acoustic communication channel. Due to the complex underwater environment, RLI communications delay is random and inevitable. At the same time, the slave UUVs fuse the successfully received RLI and measurements by on board sensors to improve its individual localisation accuracy.
In this paper, we define the navigation frame (x, y, z) as a local-level frame with three axes pointing east, north and up respectively. As the depth of UUV can be accurately measured with the on board depth sensors, so the 3D problem is converted into a 2D problem. If we assume that the RLI is transmitted from the master UUV at time step k and received by the slave UUV at time step t, according to Section 2, we know that t−k ≤ N. The nonlinear dynamics system of the slave UUVs can be described as follows:
 $$\matrix{ {{x_{t + 1}} = {x_t} + {v_t} \cdot \delta t \cdot sin{\theta _t}} \cr {{y_{t + 1}} = {y_t} + {v_t} \cdot \delta t \cdot cos{\theta _t}} \cr {{\theta _{t + 1}} = {\theta _t} + y \cdot {\omega _t} \cdot \delta t} \cr} $$
$$\matrix{ {{x_{t + 1}} = {x_t} + {v_t} \cdot \delta t \cdot sin{\theta _t}} \cr {{y_{t + 1}} = {y_t} + {v_t} \cdot \delta t \cdot cos{\theta _t}} \cr {{\theta _{t + 1}} = {\theta _t} + y \cdot {\omega _t} \cdot \delta t} \cr} $$
where x t+1, x t, y t+1, y t is the east and north components of the slave UUV location at time t, t−1, respectively. θ, v, ω are the heading angle, linear and rotational velocity of vehicle and δt is the period time of sampling. As shown in Equation (28), the location of the slave UUV updates with the output of the DR algorithm at each sample time. We define the state of system as ![]() ${\rm \;} X_k^t = {\left( {{x_t},\,{y_t},\,{\theta _t}} \right)^T}$ and the input
${\rm \;} X_k^t = {\left( {{x_t},\,{y_t},\,{\theta _t}} \right)^T}$ and the input![]() ${\rm \;} u_k^t = {\left( {{v_t},{\omega _t}} \right)^T}\!$, the state propagation equation is:
${\rm \;} u_k^t = {\left( {{v_t},{\omega _t}} \right)^T}\!$, the state propagation equation is:
 $${A_t} = \displaystyle{{\partial f} \over {\partial X_k^t}} = \left[ {\matrix{ 1 & 0 & {{v_t} \cdot \delta t \cdot cos{\theta _t}} \cr 0 & 1 & { - {v_t} \cdot \delta t \cdot sin{\theta _t}} \cr 0 & 0 & 1 \cr}} \right]\!,{G_t} = \displaystyle{{\partial f} \over {\partial u_k^t}} = \left[ {\matrix{ {\delta t \cdot sin{\theta _t}} & 0 \cr {\delta t \cdot cos{\theta _t}} & 0 \cr 0 & {\delta t} \cr}} \right]$$
$${A_t} = \displaystyle{{\partial f} \over {\partial X_k^t}} = \left[ {\matrix{ 1 & 0 & {{v_t} \cdot \delta t \cdot cos{\theta _t}} \cr 0 & 1 & { - {v_t} \cdot \delta t \cdot sin{\theta _t}} \cr 0 & 0 & 1 \cr}} \right]\!,{G_t} = \displaystyle{{\partial f} \over {\partial u_k^t}} = \left[ {\matrix{ {\delta t \cdot sin{\theta _t}} & 0 \cr {\delta t \cdot cos{\theta _t}} & 0 \cr 0 & {\delta t} \cr}} \right]$$If we define the measurements of the system as:
 $$\tilde Z_k^t = \mu _k^t {Z_k} = \mu _k^t \left[ {\matrix{ {x_k^M} \cr {y_k^M} \cr {{r_k}} \cr}} \right] + v_k^t = \mu _k^t \left[ {\matrix{ {x_k^M} \cr {y_k^M} \cr {\sqrt {{{\left( {x_k^M - {x_k}} \right)}^2} + {{\left( {y_k^M - {y_k}} \right)}^2}}} \cr}} \right] + v_k^t $$
$$\tilde Z_k^t = \mu _k^t {Z_k} = \mu _k^t \left[ {\matrix{ {x_k^M} \cr {y_k^M} \cr {{r_k}} \cr}} \right] + v_k^t = \mu _k^t \left[ {\matrix{ {x_k^M} \cr {y_k^M} \cr {\sqrt {{{\left( {x_k^M - {x_k}} \right)}^2} + {{\left( {y_k^M - {y_k}} \right)}^2}}} \cr}} \right] + v_k^t $$
where ![]() $x_k^M $,
$x_k^M $, ![]() $y_k^M $ are the east and north components of the master UUV localisation information at time k. Note that the relative range r k in
$y_k^M $ are the east and north components of the master UUV localisation information at time k. Note that the relative range r k in ![]() $\tilde Z_k^t $ is a function with the location of the slave UUV at time k, however
$\tilde Z_k^t $ is a function with the location of the slave UUV at time k, however![]() ${\rm \;} X_k^t {\rm \;} $ consists of the location at time t, r k is uncorrelated with the current state
${\rm \;} X_k^t {\rm \;} $ consists of the location at time t, r k is uncorrelated with the current state![]() $\; X_k^t $. In order to fuse the delayed measurement
$\; X_k^t $. In order to fuse the delayed measurement ![]() $\tilde Z_k^t, $ some transformations are given to obtain the observation equation. Iterate using the equation
$\tilde Z_k^t, $ some transformations are given to obtain the observation equation. Iterate using the equation![]() ${\rm \;} X_k^{t + 1} = {A_t}X_k^t + {G_t}{w_t}$, the relationship between
${\rm \;} X_k^{t + 1} = {A_t}X_k^t + {G_t}{w_t}$, the relationship between![]() $\; X_k^t {\rm \;} $ and
$\; X_k^t {\rm \;} $ and![]() ${\rm \;} X_k^k {\rm \;} $ can be obtained as:
${\rm \;} X_k^k {\rm \;} $ can be obtained as:
 $$X_k^t = \left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)X_k^k + g\left( {{w_{k + 1}}, \cdots \cdots, {w_{t - 1}}} \right) + {G_k}{w_k}$$
$$X_k^t = \left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)X_k^k + g\left( {{w_{k + 1}}, \cdots \cdots, {w_{t - 1}}} \right) + {G_k}{w_k}$$The observation equation is given as:
where the parameter matrices are defined as:
 $$\matrix{ {{B_k} = \displaystyle{{\partial h} \over {\partial X_k^k}} \displaystyle{{\partial X_k^k} \over {\partial X_k^t}}, {J_k} = \displaystyle{{\partial h} \over {\partial X_k^k}} \displaystyle{{\partial X_k^k} \over {\partial {w_k}}},} \cr {\displaystyle{{\partial z} \over {\partial X_k^k}} = \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr {\displaystyle{{ - \left( {x_k^M - {x_k}} \right)} \over {{r_k}}}} & {\displaystyle{{ - \left( {y_k^M - {y_k}} \right)} \over {{r_k}}}} & 0 \cr}} \right]\!,{\rm \;} \displaystyle{{\partial X_k^k} \over {\partial X_k^t}} = {{\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)}^{ - 1}}\!,\displaystyle{{\partial X_k^k} \over {\partial {w_k}}} = - {{\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)}^{ - 1}}{G_k}} \cr}$$
$$\matrix{ {{B_k} = \displaystyle{{\partial h} \over {\partial X_k^k}} \displaystyle{{\partial X_k^k} \over {\partial X_k^t}}, {J_k} = \displaystyle{{\partial h} \over {\partial X_k^k}} \displaystyle{{\partial X_k^k} \over {\partial {w_k}}},} \cr {\displaystyle{{\partial z} \over {\partial X_k^k}} = \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr {\displaystyle{{ - \left( {x_k^M - {x_k}} \right)} \over {{r_k}}}} & {\displaystyle{{ - \left( {y_k^M - {y_k}} \right)} \over {{r_k}}}} & 0 \cr}} \right]\!,{\rm \;} \displaystyle{{\partial X_k^k} \over {\partial X_k^t}} = {{\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)}^{ - 1}}\!,\displaystyle{{\partial X_k^k} \over {\partial {w_k}}} = - {{\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)}^{ - 1}}{G_k}} \cr}$$Based on the special structure of matrix A j, we can get the following equations:
 $$\mathop \prod \limits_{\,j = k}^t {A_j} = \left[ {\matrix{ {{I_{2 \,\times\, 2}}} & {\mathop \sum \limits_{\,j = k}^t {L_j}} \cr 0 & 1 \cr}} \right]\!\!,{\rm \; \;} {\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)^{ - 1}} = \left[ {\matrix{ {{I_{2 \,\times\, 2}}} & { - \mathop \sum \limits_{\,j = k}^t {L_j}} \cr 0 & 1 \cr}} \right]\!\!,\; \; {L_j} = \left[ {\matrix{ {{v_j} \cdot \delta t \cdot cos{\theta _j}} \cr { - {v_j} \cdot \delta t \cdot sin{\theta _j}} \cr}} \right]$$
$$\mathop \prod \limits_{\,j = k}^t {A_j} = \left[ {\matrix{ {{I_{2 \,\times\, 2}}} & {\mathop \sum \limits_{\,j = k}^t {L_j}} \cr 0 & 1 \cr}} \right]\!\!,{\rm \; \;} {\left( {\mathop \prod \limits_{\,j = k}^t {A_j}} \right)^{ - 1}} = \left[ {\matrix{ {{I_{2 \,\times\, 2}}} & { - \mathop \sum \limits_{\,j = k}^t {L_j}} \cr 0 & 1 \cr}} \right]\!\!,\; \; {L_j} = \left[ {\matrix{ {{v_j} \cdot \delta t \cdot cos{\theta _j}} \cr { - {v_j} \cdot \delta t \cdot sin{\theta _j}} \cr}} \right]$$The algorithm described above has been tested using the simulator of two UUVs, one is the master UUV and the other is the slave UUV. We show in the scanning mission the utility and the performance of our method. It is clear that the communication delay between UUVs includes two parts such as Δ = ΔT + r/V, where ΔT means the inherent process time of the WHOI micro-modem, r is the relative range,V is the transmission velocity of acoustic information, r/V is the travel time of communication packets. According to the practice experiments data in Bahr et al. (Reference Bahr, Leonard and Fallon2009a), the constant part ΔT = 6 s, and the dynamic part r/V ≤ 2 s because UUVs are close to others in a scanning mission. The sample time is 1 s, so the length of MHE estimation horizon is N = 8. In this simulation, the master UUV is equipped with a high precision INS, with equivalent localisation errors σxM = 5 m, σyM = 5 m. The slave UUVs are equipped with low precision sensors, with parameters σv = 0·2 m/s, σω = 10 0 /h and the relative range of measurement error is σr = 0·5 m.
First of all, the UUVs obtain their initial position by GPS measurement and get the global clock synchronization by PPS signal of GPS when they are on the surface. After the initialization, the MHE method directly provides the estimated position of the slave UUV underwater. In order to show the advantage of MHE, we compared the slave UUV localisation errors of DR, EKF, DEKF and MHE method as shown in Figures 3 to 6.

Figure 3. The real trajectories of the master and slave UUVs.
The two UUVs start from the same location and move within the same area during the cooperative scanning missions. The real trajectories followed by these UUVs are shown in Figure 3. Firstly we examine the case where there is no RLI exchange between UUVs. The slave UUV reckons its location independently by appropriately integrating its linear and rotational velocity which was measured by the on board low precision sensors. The trajectory by DR is shown in Figure 4, the localisation error of DR grows continuously without bound in motion. The recorded error at the end of this trial was 88 m over a travelled distance of approximately 3200 m.

Figure 4. The real and DR trajectories of slave UUV.
Next the case of UUVs exchanging RLI and performing CL continuously is examined. The trajectory is shown in Figure 5 and the MHE algorithm can obtain a good performance when dealing with the inevitable communication delay in the CL process; the maximum localisation errors are less than 10 m for the slave UUV.

Figure 5. The real and MHE trajectories of slave UUV.
Finally, we compared the localisation errors of DR, normal EKF, DEKF introduced in Section 2 and MHE introduced in Section 3, as shown in Figure 6. The location estimation by normal EKF has a significant bias from the true value, and the maximum error is almost 50 m, thus EKF is unsuitable for this scenario. Though the negative effect of communication delay can be reduced using DEKF, the localisation errors are unstable. This is caused by two factors: (1) the Kalman frame filters estimate the present state based on one-step prediction, so the results are sensitive to random measurements delay, and (2) DEKF assumes system noises to be in a Gaussian White distribution. For underwater acoustic channels, this is most certainly not the case. The MHE algorithm in this paper computes the present state estimation based on a batch of the latest arrived measurements, which can reduce the sensitivity of the estimator to the random delayed RLI, and provide a high degree of robustness in the presence of communication multiple packet delay. Additionally, MHE can estimate the errors between real practical noise and ideal Gaussian white noise as proposed earlier, which improves the localisation accuracy as shown in Figure 6.

Figure 6. The localisation errors of slave UUV by DR, EKF, DEKF, MHE algorithm.
In Figures 7 and 8, the east and north errors of the position estimated by the MHE method are plotted and compared against the ±3σ values of the position estimates' covariance. The dashed black lines represent the values associated with the covariance computed by the MHE. In these plots, the ±3σ enveloping lines define a confidence region that closely describes the magnitude of the localisation errors, the east recorded error at the end of this trial is −0·5 m, the maximum expected error is almost 8·9 m, while the north error at the end of this trial is 1 m, the maximum expected error is almost −20 m for the same distance, so the substantial improvement in localisation accuracy, achieved when the slave UUV is recording and processing RLI with MHE, is illustrated.

Figure 7. The East localisation errors of CL by MHE algorithm.

Figure 8. The North localisation errors of CL by MHE algorithm.
In practice, navigation algorithms always demand strict real-time performance. As mentioned in Zavala et al. (Reference Zavala, Laird and Biegler2008), the computation complexity of the forward Riccati decomposition strategy for the KKT system scales as O(N(n x + n w)3). In this paper, with the further exploitation of sparse band structure in the KKT matrix M, we use the direct forward-backward Riccati recursion strategy to solve the KKT system, and the computation complexity of this algorithm is roughly O(N(n x + n w)2). In order to illustrate the real-time performance of MHE method, we run the C code on a 2·13 GHz Core2-Duo processor computer with 4 GB of RAM memory, we recorded the computation time of each time step and drew the scatter diagram as shown in Figure 9. From those experiments, we can see that at each time step, the real computation time of the MHE algorithm is less than 1·7 ms, while the computation time of the DEKF and EKF algorithms are less than 0·6 ms. The computation time for the MHE is approximately three times higher than that of the EKF. So the MHE algorithm that was introduced in this paper can obtain a good real-time performance and be used in reality.

Figure 9. The computation time in seconds for each time step with MHE, DEKF, EKF algorithm.
5. CONCLUSION
In this paper, an MHE estimator is designed to deal with cooperative localisation with communication delay, which optimally combines information from both real-time sensors and delayed channels. In contrast to land-based mobile robots, due to the complex underwater environment, time delay during acoustic communication among the UUVs is inevitable. Therefore, taking into account the characteristic of the communication delay during CL, we propose a new MHE algorithm with DEKF-based arrive cost updating to solve the problem. In order to reduce the complexity of MHE, a type of Riccati recursion algorithm based on LU factorization is employed to solve the KKT system. Simulation results show that the algorithm can perform effectively in a scenario with communication delay. Considering the robustness, the algorithm proposed will present a significant practicality in cooperative localisation of MUUVs.
ACKNOWLEDGMENT
This work is supported by National Natural Science Foundation of China (No. 51379042 and No. 61203225). This work is also supported by the fundamental research funds for central universities (NO. heucf041420).