1. INTRODUCTION
Traditional spacecraft navigation uses Earth-based resources and has proved to be very reliable and robust in many successful space missions (Iess et al., Reference Iess, Asmar and Tortora2009). However, this technology requires continuous observation, and since the maximum signal delay can be up to six hours in a solar exploration, it cannot meet the needs of real time navigation, especially during the planetary, rendezvous, and landing phases. Meanwhile, the cost of Earth-based navigation is very high, lagging behind the navigation requirement of controlling deep space exploration missions in real time; a less expensive and more reliable alternative is emerging in autonomous optical navigation technology (Betto et al., Reference Betto, Rgensen, Rgensen and Denver2006).
Autonomous optical navigation has the advantages of independence, high accuracy, and real-time performance, and has become a hotspot for research in recent years (Yu et al., Reference Yu, Cui and Tian2014; Ning and Fang, Reference Ning and Fang2009; Ma et al., Reference Ma, Fang and Ning2013). Autonomous optical navigation reduces the complexity of operation and mission costs, simplifies the Earth-based support system, and greatly enhances the efficiency of deep space exploration. Even in conditions where the detector and ground communications are interrupted, it is still capable of completing orbit determination, orbit keeping, and attitude control. At present, the feasibility of optical navigation has been preliminarily validated in many deep-space missions. In the Voyager missions, key techniques for deep space navigation, including the celestial centroid-extracting algorithm, were developed (Rudd et al., Reference Rudd, Hall and Spradlin1997). Later, optical navigation was successfully conducted in the Galileo spacecraft's approach to and crossing of an asteroid. The first full application of autonomous navigation technology, though, was not realised until the Deep Space 1 mission. The main idea of autonomous optical navigation in this mission was in determining the craft's position and velocity via the optical measurement of an asteroid and background stars. In addition, the European Space Agency (ESA) used Smart-1 to verify an autonomous navigation system in deep space missions. The ESA test used an AMIE camera to take pictures of certain celestial bodies or navigation stars so as to determine the line-of-sight direction of the celestial body or astral, and then calculated the orbit of the probe (Marini et al., Reference Marini, Racca and Foing2002; Rathsman et al., Reference Rathsman, Kugelberg, Bodin, Racca, Foing and Stagnaro2005).
With rapid technological developments of high-resolution cameras, image size has become increasingly larger, as has the complexity of image processing algorithms. It is challenging to develop image-processing algorithms to meet the demands of real-time high-accuracy navigation. Traditional image processing algorithms cannot be applied directly by an autonomous navigation system because of the low on board computation capacity and the particularity of deep space (Owen, Reference Owen2011). Recently, papers have been published on the subject of autonomous optical navigation; most of them are about navigation measurement modelling and navigation filters, and few focus on image processing and extraction of navigation observables (Giannitrapani et al., Reference Giannitrapani, Ceccarelli, Scortecci and Garulli2011; Thompson et al., Reference Thompson, Bunte, Castano, Chien and Greeley2012; Shuang and Cui, Reference Shuang and Cui2008). Owen (Reference Owen2011) pointed out that useful navigation observables include the apparent diameter and centroid of the planet, the line-of-sight vector, and the angle between the horizon and the reference star. (Christian and Lightseys, Reference Christian and Lightsey2012) used binaryzation, dilation, erosion, and image closing, analysed the interconnected components and then fitted an ellipse to the planet in order to extract the planet centroid. Li et al. (Reference Li, Lu, Zhang and Peng2013) presented a detailed procedure for the extraction of navigation observables, used the Canny operator to extract planet edges, and then fitted the planet ellipse with edge points. The accuracies achieved by these methods are able to meet the requirements of deep-space autonomous navigation. However, higher accuracy navigation observables are needed to achieve a more reliable optical navigation, and less computation in the image-processing algorithm is necessary to implement a faster optical navigation.
In this study, we developed a simple and effective image-processing algorithm for extracting a planet centroid. The planet centroid is an important parameter with which the spacecraft state can be estimated after the navigation filter and system dynamics equations are established. It is assumed that the perspective projection of a target planet body forms an ellipse on the image plane. In the remainder of this paper, Section 2 briefly presents the principle of autonomous optical navigation and the image processing algorithms. Section 3 presents a method for segmenting the planet image block from the whole image so as to eliminate noise and to reduce the computation burden. Section 4 introduces an algorithm to extract sub-pixel real edge points. Section 5 describes the method used for ellipse fitting based on a set of real edge points and the centroid computation formula. Section 6 validates the algorithm with experiments for detection accuracy. Section 7 gives the conclusions.
2. PRINCIPLE OF AUTONOMOUS OPTICAL NAVIGATION
Here, autonomous optical navigation is based on the extraction of the planet centroid from the planet images captured by image sensors. The principles of autonomous optical navigation are described as follows.
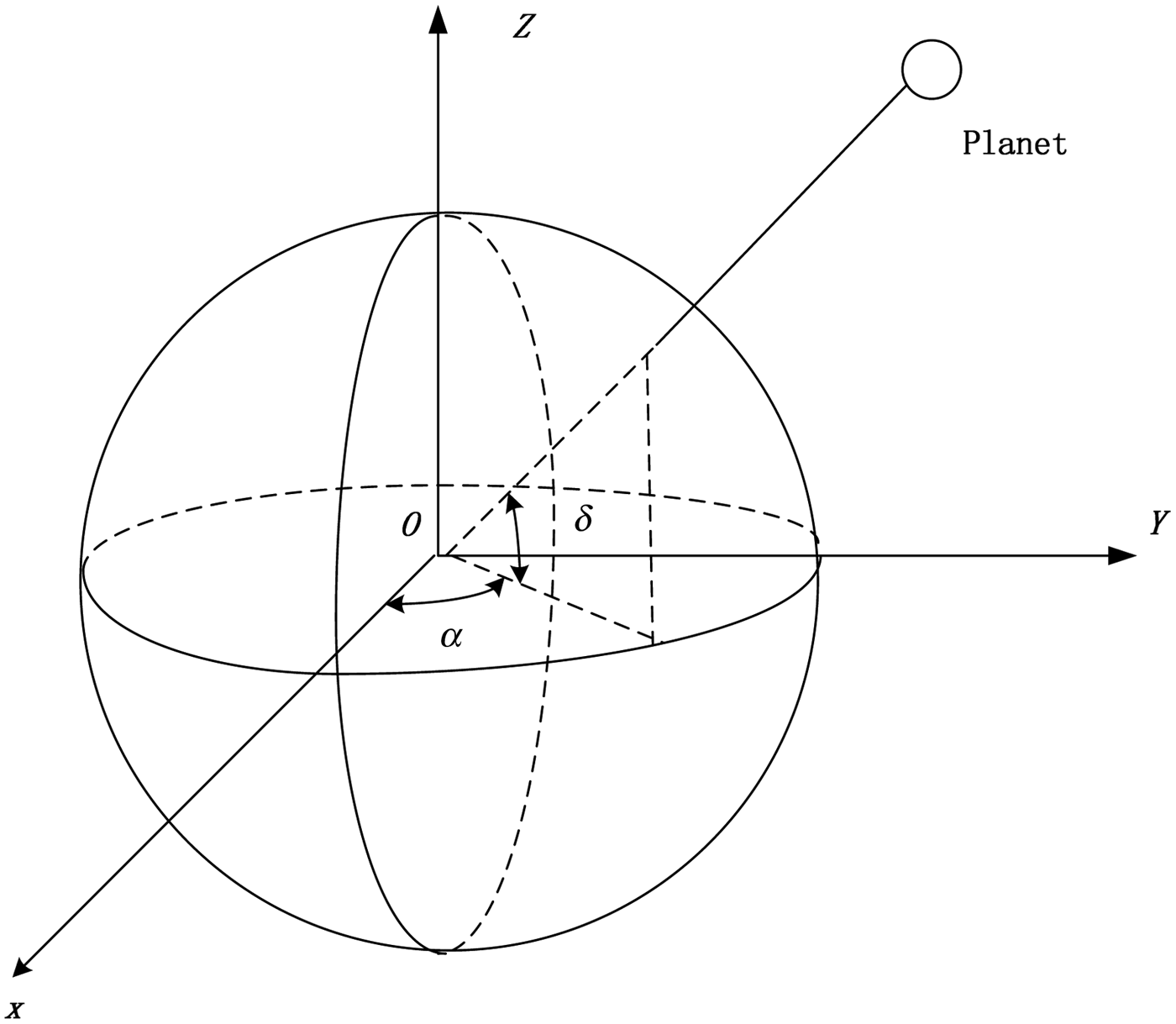
The position of a planet in celestial coordinate system OXYZ is described by right ascension α and declination δ (Figure 1). The planet unit vector e I in an inertial frame can be expressed as:
 $${e_I} = \left[ {\matrix{ {\cos \alpha \cos \delta} \cr {\sin \alpha \cos \delta} \cr {\sin \delta} \cr}} \right]$$
$${e_I} = \left[ {\matrix{ {\cos \alpha \cos \delta} \cr {\sin \alpha \cos \delta} \cr {\sin \delta} \cr}} \right]$$
Figure 1. The planet coordinates in celestial coordinate system.
The planet image captured by a detector (usually a Charge-Coupled Device (CCD) or Complementary Metal-Oxide Semiconductor (CMOS) array in this case) can be described by a set of [x p, y p] in the image plane frame Oxy (Figure 2). According to the geometric relations shown in Figure 2, the line-of-sight direction to an object is given by the following equation (Christian and Lightsey, Reference Christian and Lightsey2012):
 $${e_c} = \displaystyle{1 \over {\sqrt {x_p^2 + y_p^2 + {\,f^2}}}} \left[ {\matrix{ { - {x_p}} \cr { - {y_p}} \cr f \cr}} \right]$$
$${e_c} = \displaystyle{1 \over {\sqrt {x_p^2 + y_p^2 + {\,f^2}}}} \left[ {\matrix{ { - {x_p}} \cr { - {y_p}} \cr f \cr}} \right]$$where f is the camera focal length and e c is the unit vector of the line-of-sight described in the camera coordinate system O ′x cy cz c. The line-of-sight vector is then rotated from the camera frame to the inertial frame:
in which ![]() $T_C^B $ rotates a vector from the camera frame to the spacecraft body frame, and
$T_C^B $ rotates a vector from the camera frame to the spacecraft body frame, and ![]() $T_B^I $ rotates a vector from the spacecraft body frame to the inertial frame. The transformation matrices
$T_B^I $ rotates a vector from the spacecraft body frame to the inertial frame. The transformation matrices ![]() $T_C^B $ and
$T_C^B $ and ![]() $T_B^I $ include information on the attitude and position of the spacecraft. The unit vector e I can be obtained by referring to the ephemeris. Because the camera's focal length f is known to be fixed for a known camera, the main challenge to acquiring the line-of-sight unit vector e c is to define the centroid (x, y) of the planet (Owen et al., Reference Owen, Duxbury, Acton, Synnott, Riedel and Bhaskaran2008).
$T_B^I $ include information on the attitude and position of the spacecraft. The unit vector e I can be obtained by referring to the ephemeris. Because the camera's focal length f is known to be fixed for a known camera, the main challenge to acquiring the line-of-sight unit vector e c is to define the centroid (x, y) of the planet (Owen et al., Reference Owen, Duxbury, Acton, Synnott, Riedel and Bhaskaran2008).

Figure 2. Geometry of planet imaging.
3. PLANET SEGMENTATION
On a deep-space image, a planet accounts for a part of the whole image, as does the noise of other stars and objects. To process only a planet image block can save computation load and time.
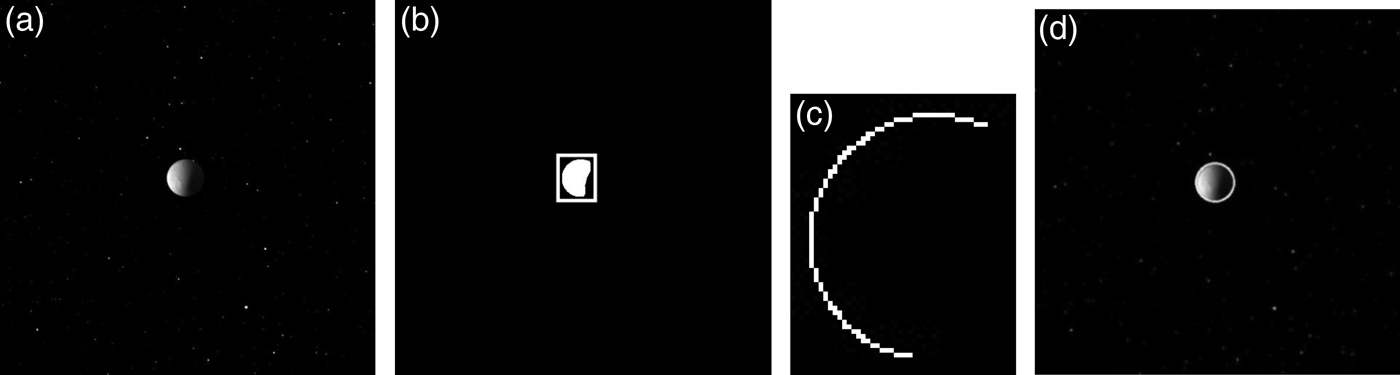
First, conducting threshold segmentation to simplify a raw image into a binary image helps speed up the subsequent image processing. Assuming that a threshold value τ is selected, creating a binary image would check the pixel value at each pixel point. Each pixel in intensity above τ is set to 255 (white) and below τ is set to 0 (black) (Javidi et al., Reference Javidi, Li, Fazlollahi and Horner1995). The pixels with a value of 255 are considered to be in the “foreground” in which the planet information is contained. Figure 3(b) shows the binary image of the planet Mars with a threshold value τ = 30.

Figure 3. Image of Mars and the results of a planet segmentation (a) Image of Mars; (b) Mars' binary image; (c) background stars removed by an opening operator; (d) foreground Mars' area found in the whole image.
Second, morphological opening is operated to remove the noise of secondary stars and objects. This operation uses erosion first and then dilation (Haralick et al., Reference Haralick, Sternberg and Zhuang1987).
In general, an opening operation can smooth the outline of an object in the image, and it eliminates zigzags. When applied in deep space images, small stars/objects can be removed effectively, and the edges of a planet become smooth.
Using a structure element S, one can carry out the opening on image A according to Kemper (Reference Kemper1998):
where ![]() ${\!\circ} $ is for the opening operator,
${\!\circ} $ is for the opening operator, ![]() ${\rm \ominus} $ is the erosion operator, and
${\rm \ominus} $ is the erosion operator, and ![]() $ \oplus $ is the dilation operator.
$ \oplus $ is the dilation operator.
Figure 3(c) shows the opening operator's result. It can be seen that the background stars have been cleared up. Figure 4 is the local planetary binary image resulting from an opening operator. Figure 4(a) shows noise in the background at the edge of the planet. Figure 4(b) shows the result of the opening operation, in which the noise is cleaned out and the edges become smooth.

Figure 4. Local planetary binary image and the result of the opening operation (a) local planetary binary image (b) the result of the opening operator.
Third, a planet image block is segmented from the whole image. As shown in Figure 3(c), noise has been cleaned up on the image. The segmentation includes the following steps.
(1) To find the start line x 1 and end line x 2 with pixel value 255 at direction x in the whole image;
(2) To find the start column y 1 and end column y 2 with pixel value 255 at direction y in the whole image;
(3) The area surrounded by point (x 1, y 1) and point (x 2, y 2) is defined as the planet image block represented by the white frame in Figure 3(d).
Now, a planet image block is successfully segmented. Next, edge detection will be applied on just the block. All unwanted information is discarded, and the image processing load and time can be greatly reduced.
4. SUB-PIXEL EDGE DETECTION
Edge detection employs local operators to compute approximately the first derivative of grey level gradient on an image in the spatial domain. Locations in the local maximum of the first derivative will be considered to be the edge points. Ideally, an edge detection algorithm will be able to determine all edges and edge points accurately in the position. At present, many such algorithms have been developed at the pixel or sub-pixel level. Pixel-level edge detections, including Prewitt, Sobel, Laplacian of Gaussian (LOG), and Canny operators are capable of detecting edges quickly but with low accuracy (Ding and Goshtasby, Reference Ding and Goshtasby2001; Wang Reference Wang2007; Hou and Wei, Reference Hou and Wei2002). Li et al. (Reference Li, Lu, Zhang and Peng2013) detected the edges at pixel level with the Canny operators. All the edges may be detected in this way, but the position accuracy is low. Sub-pixel level methods, such as interpolation and the Zernike method, can enhance the accuracy but require a longer runtime (Wee and Paramesran, Reference Wee and Paramesran2007). Ying-Dong et al. (Reference Ying-Dong, Cheng-Song, San-Ben and Jin-Quan2005) propose an approach combining the pixel-level method with the sub-pixel level method to detect an object edge using the Sobel-Zernike moments operator.
We propose an algorithm of Prewitt-Zernike moments edge detection and apply it in planet-containing images. The Prewitt-Zernike moments edge detection is an algorithm that first detects possible edges with the Prewitt operator and then relocates them with possible edges to sub-pixel accuracy determined by the Zernike moments. To save computation while retaining real edges, and before possible edges detected by the Prewitt operator are relocated to sub-pixel accuracy by Zernike moments, pseudo-edges in the backlit shade areas are removed. Our proposed edge detection algorithm consists of three steps. First, the Prewitt operator is used to detect approximately all possible edge points. Second, pseudo-edges in the backlit shade areas are removed. Third, the Zernike moments operator is used to relocate the real edge points to sub-pixel accuracy.
4.1. Prewitt Edge Detection
A Prewitt operator detects edges by calculating partial derivatives in 3 × 3 neighbourhoods and by smoothing out noise. It is relatively simpler than other operators such as the LOG operator, Canny operator, and so on. In our example, the planet image block is very simple (Figure 5(a)), in which the Prewitt operator was used to detect edges. The pre-processing steps (the procedure listed in Section 3) eliminate noise and segment the planet image block. After pre-processing, the Prewitt operator is used to detect the edge. The partial derivatives in horizontal direction F h and vertical direction F v are given according to Kuo et al. (Reference Kuo, Lee and Liu1997):

Figure 5. Edge detection algorithm applied to planet image block (a) planet image block; (b) result by Prewitt operator; (c) pseudo-edges removal; (d) relocating the edges with sub-pixel accuracy.
Then, the edge gradient magnitude M(x, y) and direction θ(x, y) are determined as follows:
Then the threshold value t is selected, if it is satisfied that
Hereafter, a point means an edge point. All the points must be marked. Figure 5(b) shows the result from Prewitt edge detection, which obviously includes the pseudo-edges. The next section describes removal of these pseudo-edges.
4.2. Pseudo-edges removal
Pseudo-edges usually occur at the border between a sunlight face and backlit face (Thompson et al., Reference Thompson, Bunte, Castano, Chien and Greeley2012). In order to extract a planet centroid to high accuracy, real edges must be distinguished from pseudo-edges. Pseudo-edges can be detected by calculating the angle between the solar direction and the gradient direction of edges. In fact, the angle between the gradient direction of edges and the solar direction is within 90°. The main difficulty is to determine the direction to the sun, which may be measured directly by an instrument such as a Sun sensor. Given the planet's edge gradient vector g and the direction n to the Sun, the following equation can be satisfied (Li et al., Reference Li, Lu, Zhang and Peng2013):
which can be simplified as:
Figure 5(c) shows successful removal of pseudo-edges; the green arrows stand for the edge gradient vectors and the red ones are the solar light direction.
4.3. Sub-pixel edges relocated
In Section 4.2, real edges are detected to just pixel-level accuracy. In order to reach a higher accuracy of planet centroid, a Zernike moments operator is used to relocate edges to sub-pixel accuracy among all the real edge points.
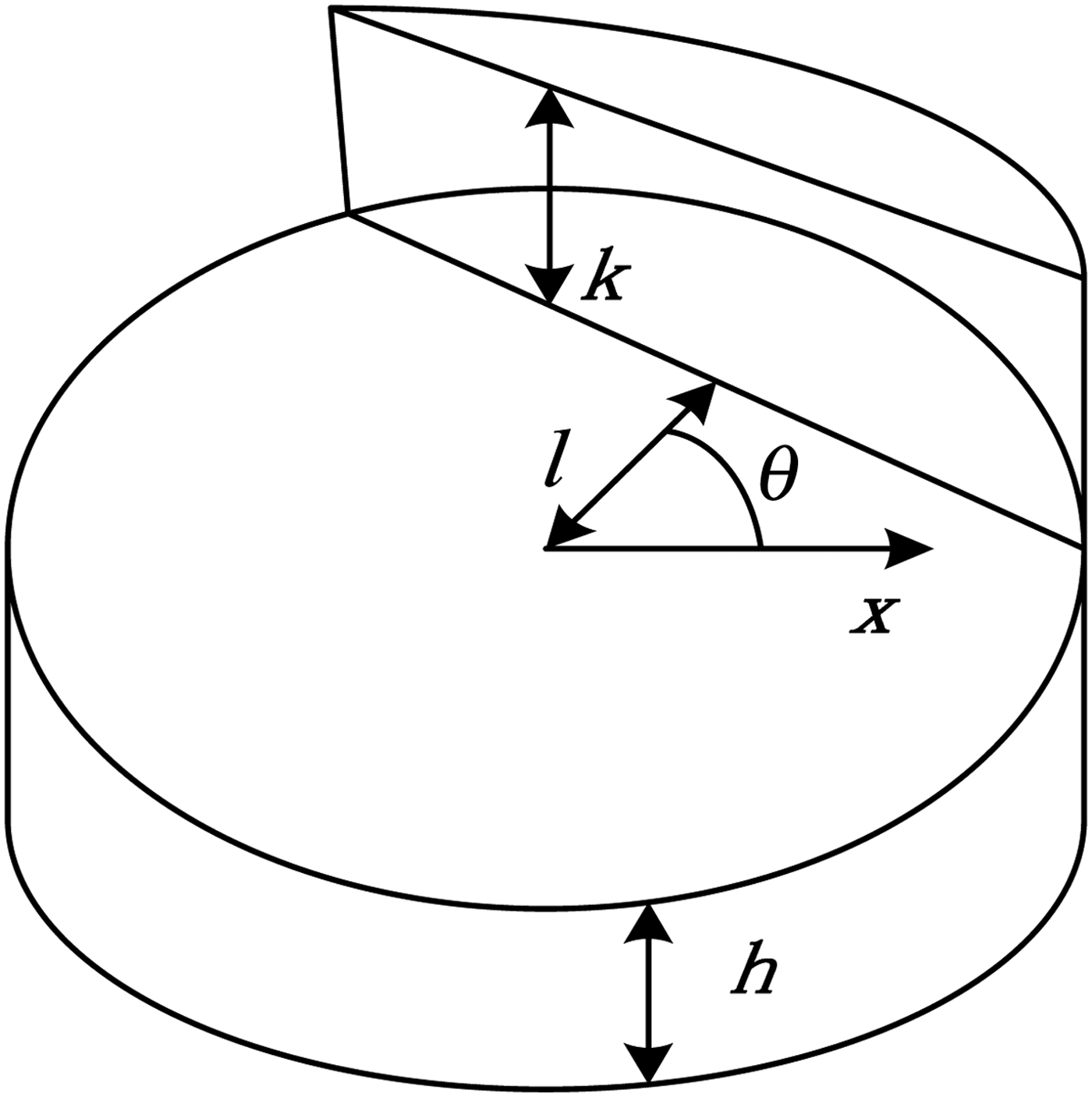
Edges of a continuous ideal image can be seen in a step model as shown in Figure 6, in which h is the background grey level, k is the step height, l is the perpendicular distance between the actual edge and the centre, and θ is the angle between the edge and horizontal line and satisfied as ![]() $\theta \in ( - \displaystyle{\pi \over 2},\displaystyle{\pi \over 2})$.
$\theta \in ( - \displaystyle{\pi \over 2},\displaystyle{\pi \over 2})$.

Figure 6. The two-dimensional sub-pixel step-model.
Zernike moments for an image f(x, y) are defined as per Ghosal and Mehrotra (Reference Ghosal and Mehrotra1993):
 $${A_{nm}}\, = \,\displaystyle{{n + 1} \over {\rm \pi }}{\int\int\limits_{{x^2} + {y^2} \le 1}} {\,f\left( {x,y} \right)V_{nm}^ \ast \left( {\rho ,\theta } \right)dxdy} $$
$${A_{nm}}\, = \,\displaystyle{{n + 1} \over {\rm \pi }}{\int\int\limits_{{x^2} + {y^2} \le 1}} {\,f\left( {x,y} \right)V_{nm}^ \ast \left( {\rho ,\theta } \right)dxdy} $$where (n + 1)/π is a normalisation factor. In discrete form, A nm can be expressed as
Equation (13) shows that in a discrete image, the neighbourhood of an image point should be mapped onto the interior of a unit circle for evaluating Zernike moments A nm of the point. The complex polynomials V nm (ρ, θ) can be expressed in polar coordinates as
where ![]() $V_{nm}^\ast $ and V nm are conjugate and R nm (ρ, θ) is a radial polynomial defined as
$V_{nm}^\ast $ and V nm are conjugate and R nm (ρ, θ) is a radial polynomial defined as
 $${R_{nm}}\left( \rho \right) = \sum \nolimits {{{{\left( { - 1} \right)}^s}(n - s)!{\rho ^{n - 2s}}} \over {s!(\displaystyle{{n + \left\vert m \right\vert} \over 2} - s)!(\displaystyle{{n - \left\vert m \right\vert} \over 2} - s)!}}$$
$${R_{nm}}\left( \rho \right) = \sum \nolimits {{{{\left( { - 1} \right)}^s}(n - s)!{\rho ^{n - 2s}}} \over {s!(\displaystyle{{n + \left\vert m \right\vert} \over 2} - s)!(\displaystyle{{n - \left\vert m \right\vert} \over 2} - s)!}}$$If the image is rotated by an angle ϕ counterclockwise, the Zernike moments of the rotated image would be
Therefore, Zernike moments require a phase shift on rotation while their magnitudes remain constant. For calculating edge parameters l and θ, the two masks A 11 and A 20 should be deduced. According to Equations (14) and (15), the orthogonal complex polynomials can be written as:
The unit circle in Figure 7 is divided into 5 × 5 grids, and masks are calculated when integrating ![]() $V_{11}^\ast, V_{20}^\ast $ on a dashed area of every grid (Ying-Dong et al., Reference Ying-Dong, Cheng-Song, San-Ben and Jin-Quan2005).
$V_{11}^\ast, V_{20}^\ast $ on a dashed area of every grid (Ying-Dong et al., Reference Ying-Dong, Cheng-Song, San-Ben and Jin-Quan2005).

Figure 7. Circular kernel defined for a 5 × 5 pixel area.
Convolving these masks with the image points can obtain Zernike moments as shown in Figures 8 and 9. The relationship between the Zernike moments of the original image A 11, A 20 and rotated image A′11, A′20 can be given as

Figure 8. Mask of A 11.

Figure 9. Mask of A 20.
The following equations can be deduced in the theory of Zernike moments (Ghosal and Mehrotra, Reference Ghosal and Mehrotra1993):
 $$A_{11}^{\prime} = \int\int\limits_{{x^2} + {y^2} \le 1} {\,f^{\prime}\left( {x,y} \right)\left( {x - jy} \right)dxdy} = \displaystyle{2k{\left( {1 - {l^{2}}} \right)}^{3\big/2} \over 3}$$
$$A_{11}^{\prime} = \int\int\limits_{{x^2} + {y^2} \le 1} {\,f^{\prime}\left( {x,y} \right)\left( {x - jy} \right)dxdy} = \displaystyle{2k{\left( {1 - {l^{2}}} \right)}^{3\big/2} \over 3}$$ $$A_{20}^{\prime} = \int\int\limits_{{x^{2}} + {y^{2}} \le 1} {\,f^{\prime}\left( {x,y} \right)\left( {2{x^{2}} + 2{y^{2}} - 1} \right)dxdy} = \displaystyle{{2kl{\left( {1 - {l^2}} \right)}^{3\big/2}} \over 3}$$
$$A_{20}^{\prime} = \int\int\limits_{{x^{2}} + {y^{2}} \le 1} {\,f^{\prime}\left( {x,y} \right)\left( {2{x^{2}} + 2{y^{2}} - 1} \right)dxdy} = \displaystyle{{2kl{\left( {1 - {l^2}} \right)}^{3\big/2}} \over 3}$$
where f′(x, y) is the rotated image. When the edge is rotated by an angle −θ, it could be aligned in parallel to the y-axis so that 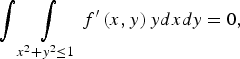 $\int\int\limits_{{x^2} + {y^2} \le 1} {f'\left( {x,y} \right)ydxdy} = 0,$ and it becomes the imaginary component of A′11 and can be expressed as
$\int\int\limits_{{x^2} + {y^2} \le 1} {f'\left( {x,y} \right)ydxdy} = 0,$ and it becomes the imaginary component of A′11 and can be expressed as
So,
Solving Equations (20) and (21), the edge parameter l can be given as:
And the sub-pixel edge detection formula is given as:
where (x s, y s) is the sub-pixel point of the edge.
5. ELLIPSE FITTING
The perspective projection of a sphere or ellipsoid forms an ellipse on an image plane. Once candidate edge points are found, an ellipse must be fitted to this data set. The details of this ellipse fitting process are discussed below.
5.1. Robust model fitting
The first useful ellipse fitting is a direct least-square algorithm developed by Fitzgibbon et al. (Reference Fitzgibbon, Pilu and Fisher1999). Any conic section may be described by the following implicit quadratic equation:
where [x i, y i] is a point on the conic section, a = [A B C D E F]T, and x i = ![]() ${\left[ {x_i^2 \; {x_i}{y_i}\; y_i^2 \; {x_i}\; {y_i}\; 1} \right]^T}$. The conic will be an ellipse if the coefficients of the equation satisfy 4AC − B 2 > 0. The form allows the constants to be scaled arbitrarily such that the ellipse inequality constraint may be rewritten as an equality constraint:
${\left[ {x_i^2 \; {x_i}{y_i}\; y_i^2 \; {x_i}\; {y_i}\; 1} \right]^T}$. The conic will be an ellipse if the coefficients of the equation satisfy 4AC − B 2 > 0. The form allows the constants to be scaled arbitrarily such that the ellipse inequality constraint may be rewritten as an equality constraint:
In general, a point detected by the edge detection algorithm mentioned in Section 4 does not lie exactly on the ellipse, and F(a, x i) ≠ 0 because of imaging noise. Therefore, Fitzgibbon et al. (Reference Fitzgibbon, Pilu and Fisher1999) proposed an optimisation method using the square of model-fit residuals:
where G = [x 1x 2…x n]T, the equality constraint of Equation (28) can be rewritten in vector form
 $$4AC - {B^2} = \; {a^T}\left[ {\matrix{ {\matrix{ {\; 0} & {\; 0} & {\; 2} \cr {\; 0} & { - 1} & {\; 0} \cr {\; 2} & {\; 0} & {\; 0} \cr}} & {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \cr {\matrix{ {\; 0\; \;} & {0\;} & {\; 0} \cr {\; 0\; \;} & {0\;} & {\; 0} \cr {0\;} & {0\;} & {\; 0} \cr}} & {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \cr}} \right]a = \; {a^T}Ha = 1$$
$$4AC - {B^2} = \; {a^T}\left[ {\matrix{ {\matrix{ {\; 0} & {\; 0} & {\; 2} \cr {\; 0} & { - 1} & {\; 0} \cr {\; 2} & {\; 0} & {\; 0} \cr}} & {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \cr {\matrix{ {\; 0\; \;} & {0\;} & {\; 0} \cr {\; 0\; \;} & {0\;} & {\; 0} \cr {0\;} & {0\;} & {\; 0} \cr}} & {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \cr}} \right]a = \; {a^T}Ha = 1$$If the equality of Equation (29) is adjoined to an objective function with a Lagrange multiplier, then
The solution to this optimisation problem is the following rank-deficient generalised eigenvalue problem
Substituting this solution into the objective function shows that
which means that the optimal solution occurs at the minimal positive eigenvalue (Fitzgibbon et al., Reference Fitzgibbon, Pilu and Fisher1999). The solution to Equation (32) yields exactly a positive eigenvalue. This positive eigenvalue corresponds to the eigenvector that is the solution to a. As noise may exist at the edge points, it is difficult to determine exact analytic solutions directly. Christian and Lightsey (Reference Christian and Lightsey2012) used the M-Estimator Sample Consensus (MSAC) algorithm to eliminate outliers in the edge points set using least-square ellipse-fitting and found that it was a robust method for fitting the elliptical model to the edge points. We adapted the MSAC algorithm to eliminate outliers so as to fit the elliptical model at the edge points.
5.2. Centroid calculation
Transformation from coefficients of an implicit conic equation into the standard ellipse parameters is a well-known classical geometry and given by:
 $$a = \; \sqrt {\displaystyle{{2\left[ {A{E^2} + C{D^2} - BDE + F\left( {{B^2} - 4AC} \right)} \right]} \over {\left( {{B^2} - 4AC} \right)\left[ {\sqrt {{{\left( {A - C} \right)}^2} + {B^2}} - A - C} \right]}}}$$
$$a = \; \sqrt {\displaystyle{{2\left[ {A{E^2} + C{D^2} - BDE + F\left( {{B^2} - 4AC} \right)} \right]} \over {\left( {{B^2} - 4AC} \right)\left[ {\sqrt {{{\left( {A - C} \right)}^2} + {B^2}} - A - C} \right]}}}$$ $$b = \; \sqrt {\displaystyle{{2\left[ {A{E^2} + C{D^2} - BDE + F\left( {{B^2} - 4AC} \right)} \right]} \over {\left( {{B^2} - 4AC} \right)\left[ { - \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} - A - C} \right]}}}$$
$$b = \; \sqrt {\displaystyle{{2\left[ {A{E^2} + C{D^2} - BDE + F\left( {{B^2} - 4AC} \right)} \right]} \over {\left( {{B^2} - 4AC} \right)\left[ { - \sqrt {{{\left( {A - C} \right)}^2} + {B^2}} - A - C} \right]}}}$$ $$\phi = \left\{ {\matrix{ {0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; B = 0\; {\rm and}\; A \lt C} \cr {\matrix{ {\displaystyle{\pi \over 2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; B = 0\; {\rm and}\; A \gt C\;} \cr {\displaystyle{1 \over 2}{{\it cot} ^{ - 1}}\left( {\displaystyle{{A - C} \over B}} \right)\; \; \; \; \; \; \; \; \; \; \; \; B \ne 0\; {\rm and}\; A \lt C} \cr {\displaystyle{\pi \over 2} + \displaystyle{1 \over 2}{{\it cot} ^{ - 1}}\left( {\displaystyle{{A - C} \over B}} \right)\; \; \; \; B \ne 0\; {\rm and}\; A \gt C} \cr}} \cr}} \right.$$
$$\phi = \left\{ {\matrix{ {0\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; B = 0\; {\rm and}\; A \lt C} \cr {\matrix{ {\displaystyle{\pi \over 2}\; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; \; B = 0\; {\rm and}\; A \gt C\;} \cr {\displaystyle{1 \over 2}{{\it cot} ^{ - 1}}\left( {\displaystyle{{A - C} \over B}} \right)\; \; \; \; \; \; \; \; \; \; \; \; B \ne 0\; {\rm and}\; A \lt C} \cr {\displaystyle{\pi \over 2} + \displaystyle{1 \over 2}{{\it cot} ^{ - 1}}\left( {\displaystyle{{A - C} \over B}} \right)\; \; \; \; B \ne 0\; {\rm and}\; A \gt C} \cr}} \cr}} \right.$$where (x, y) is the coordinate of the ellipse centre, a and b stand for the semi-major axis and semi-minor axis of the ellipse; and φ is the angle from the x-axis to the major ellipse axis. Therefore, an ellipse can be well described with the above five parameters. With these parameters, we can easily compute the line-of-sight vector from the spacecraft to the centroid of a target celestial body with Equation (2).
6. EXPERIMENTS
Experiments were performed to validate the detection accuracy for the algorithm. First, a computer-generated standard circle with noise was used to test the accuracy of the edge-detecting algorithm in Prewitt-Zernike moments. Second, real images obtained from deep-space missions were used for the validation. Lastly, the synthetic simulated images were applied to test the accuracy of the image-processing algorithm.
The experiments are shown in Figure 10(a). The size of the image is 256 × 256 in pixels, the centre of the circle is at (128·0, 128·0), and the radius is 100·0 pixels. To robustly withstand noise, Gaussian white noise with variance σ = 0·01 was added to the image. We adapted the method of Li et al. (Reference Li, Lu, Zhang and Peng2013), in which the Canny operator was used to locate the edge points, then used the sub-pixel edge detection methods of Polynomial interpolation and the Gauss surface fitting technique to relocate the sub-pixel edge points for comparing (Ye et al., Reference Ye, Fu and Poudel2005; Hermosilla et al., Reference Hermosilla, Bermejo, Balaguer and Ruiz2008). In addition, our method was applied to locate the edge points, including Prewitt-Zernike moments.

Figure 10. A standard circle with noise and the results of edge detection: (a) Standard circle with noise; (b) Edge detection result by method of Li et al. (Reference Li, Lu, Zhang and Peng2013); (c) Edge detection by the method proposed in this paper.
Figure 11 shows the absolute errors of edge locations detected in Prewitt-Zernike moments, the Polynomial interpolation method, and the Gauss surface fitting technique. The Root Mean Square (RMS) of edge detection in the Prewitt-Zernike moments is 0·14 pixels, while the RMS of the Polynomial interpolation method and Gauss surface fitting technique are 0·29 and 0·23 pixels respectively. The test result shows the Prewitt-Zernike moments have a higher accuracy than the other sub-pixel edge detection methods of Polynomial interpolation and Gauss surface fitting technique, and is more robust against Gaussian white noise. Although a sub-pixel edge detection in Prewitt-Zernike moments can reach a higher accuracy, the computation load of Prewitt-Zernike moments is still great. In order to cope with the problem, we segmented the planet image block from the whole image first, processed the edge detecting algorithm on the block only, removed fake edge points, and relocated the real edge with Prewitt-Zernike moments at sub-pixel accuracy. In this process, unnecessary sub-pixel relocating operations are reduced, focusing only on the real edges with the sub-pixel relocating algorithm in Prewitt-Zernike moments. Therefore, a more accurate planet centroid can be calculated.

Figure 11. The absolute errors of edge location for standard circle image.
In order to verify the effectiveness of the algorithm proposed, we used real raw image data that came from the Cassini-Huygens mission. The image was taken in visible light with the Cassini spacecraft wide-angle camera on 9 October 2008, at approximately 83 000 km (52 000 miles) from Enceladus, the sixth largest moon of Saturn, as seen in Figure 12(a). First, we isolated the moon image blocks in the whole images adapting the segmentation algorithm. As seen in Figure 12(b), the image block of the moon has been successfully shown as a white rectangle. After that, the edge detection method described in Section 4 was used to extract the sub-pixel edge points of the moon. The pseudo-edges at the backlit face of the moon were removed by calculating the angle between the solar direction and the gradient direction of edges. The solar direction was determined by a sun sensor. However, due to possible lack of data from the sensor, the solar direction has to be judged by visual inspection. As seen in Figure 12(c), the real edges of the moon were successfully detected. Finally, ellipses were fitted to the moon. As the true coordinate of the moon centroid in the real raw image was unknown, the accuracy could not be evaluated. In the next experiment, synthetic simulated images close to the real flyby raw images are utilised to verify the accuracy of the image-processing algorithm.

Figure 12. Planet centroid extracting algorithm applied to real raw image from Cassini-Huygens mission (a) Raw image of Enceladus; (b) Segmentation; (c) Extract of the real sub-pixel edges; (d) Earth with best ellipse.
A synthetic simulated image is simulated by Celestia software, open-source software for astronomical works supported by NASA Technology. The outer space environment, the atmosphere of the planet surface, and the texture of the planet simulated with the software are very similar to the corresponding real ones (Celestia, 2015). In order to test the accuracy of the planet centroid, five images of Mercury, Uranus, Venus, Jupiter, and Earth were simulated as shown in Figures 13(a), (b), (c), (d) and 14(a), respectively. The complete image processing algorithms developed in this study were applied to the five planets at different sun azimuth angles, surface textures, and lighting and atmospheric conditions. The Earth image was used as an example to display the procedure of the algorithm we proposed.

Figure 13. Planet images simulated by Celestial software.
As indicated in Figure 14, the planet image block of the Earth is successfully segmented, the pseudo-edges removed, the real edges detected, the edge points relocated to sub-pixel accuracy, a best ellipse fitted to the planet, and finally, the centroid coordinate of the planet obtained with Equation (33). As the planet centroid in the simulated image can be positioned accurately in advance, errors of planet centroid can be calculated easily. The edge points were detected by Prewitt-Zernike moments, the Polynomial interpolation method, the Gauss surface fitting technique, and then were fitted to an ellipse. The errors that occurred in the three methods are shown in Figure 15.

Figure 14. Simulating the Earth image with the planet centroid extracting algorithm.

Figure 15. Extracting errors of planet centroid.
Figure 15 shows that the maximum errors of the three methods were 0·35, 0·66 and 0·56 pixels, and the RMS were 0·29, 0·51 and 0·43 pixels, respectively. The method in Prewitt-Zernike moments is more accurate and stable than those in the Polynomial interpolation and Gauss surface fitting. Assuming the focal length of camera f = 200 mm, the angle of view field θ = 3·5°, and scale factor K x = K y = 83·8 pixel/mm, then the maximum observation error of the line-of-sight vector from camera to planet centroid in our proposed method is 2·1 × 10−5 rad, which easily meets the requirements of deep-space autonomous navigation.
7. CONCLUSION
To meet the high accuracy and fast processing demands of deep-space autonomous navigation, a new image-processing algorithm is proposed to extract the centroid of a planet. In particular, a simple and effective planet segmentation algorithm was developed to eliminate noise and reduce computation load. Meanwhile, a sub-pixel edge-detecting algorithm based on the Prewitt-Zernike moments is developed to detect edge points of planets at the sub-pixel level. Both real flyby images from the Voyager mission and corresponding simulated images were used to verify the performance of the algorithm. Simulating a standard circle with noise shows that the precision of the proposed Prewitt-Zernike moments operators achieved 0·14 pixels in edge location accuracy. In addition, experiments on a real raw image proved that the algorithm is effective, as the planet was successfully segmented from the real raw image and an ellipse was well fitted to the planet. In addition, experiments on planet image simulations indicate that the accuracy of the planet centroid reached as high as 0·3 pixels and the accuracy of the line-of-sight vector to 2·1 × 10−5 rad. Therefore, with the higher-accuracy positioning for a planet centroid, the reliability of deep-space autonomous optical navigation will be improved.
ACKNOWLEDGEMENTS
The work described in this paper was supported by: the National Basic Research Program of China 973 Program (Grant NO. 2014CB744201), National Natural Science Foundation of China (NSFC) (Grant NO.41371430 and 91438111). The author fully appreciates their financial support.