1. INTRODUCTION
In dense urban environments, buildings and other obstacles block the direct line-of-sight to many satellites. Furthermore, there are many flat and reflective surfaces that reflect GNSS signals. Reception of these reflected signals results in significant positioning errors via two separate mechanisms.
Non-line-of-sight (NLOS) reception is where the direct signal is blocked and the signal is received only via reflections. This results in a pseudo-range measurement error equal to the additional path delay, the difference between the length of the path taken by the reflected signal and the (blocked) direct path between the satellite and user antenna. This error is always positive and, although typically tens of metres, is potentially unlimited. Signals received via distant tall buildings can exhibit errors of more than a kilometre. The ranging error from carrier-phase measurements is similar to the pseudo-range error. NLOS signals can be nearly as strong as the directly received signals, but can also be very weak. As high-sensitivity receivers can acquire much weaker signals, their use can significantly increase the number of NLOS signals received.
Where the signal is received through multiple paths, this is known as multipath interference. The reflected signals distort the code correlation peak within the receiver such that the code phase of the direct line-of-sight (LOS) signal cannot be accurately determined by equalising the power in the early and late correlation channels. The resulting code tracking error depends on the receiver design as well as the direct and reflected signal strengths, path delay and phase difference, and can be up to half a code chip (Van Nee, Reference Van Nee1992; Braasch, Reference Braasch, Parkinson and Spilker1996; Groves, Reference Groves2013). Carrier-phase tracking errors are limited to a quarter of a wavelength (assuming the direct LOS signal is stronger than the reflections).
NLOS reception and multipath interference are often grouped together as “multipath”. However, it is better to treat them as separate phenomena as they not only produce different ranging errors, but also require different approaches to mitigating the errors. NLOS reception and multipath interference can also occur together whenever a signal is received via multiple reflected paths but not directly.
Several methods exist for mitigating multipath interference and NLOS reception with various limitations. Techniques may be classified as antenna-based, receiver-based and post-receiver, and may be used in combination (Groves, Reference Groves2013). An antenna with good polarisation discrimination can reduce the positioning errors due to multipath interference by an order of magnitude by attenuating reflected signals. However, this has little direct effect on the ranging errors due to NLOS reception. Ground planes, choke rings and beam-forming antenna arrays can bring further improvements, but are usually bulky and expensive. Receiver-based techniques that sharpen the peak of the code correlation function, often deploying additional correlation channels, can significantly reduce the pseudo-range measurement errors due to multipath interference but have no effect on NLOS signal reception. They also increase the cost and power consumption of the receiver.
Post-receiver techniques operate using the pseudo-range, carrier-phase and carrier-power-to-noise density ratio, C/N 0, measurements prior to the position calculation. Multipath interference may be detected and mitigated by comparing measurements on different frequencies from the same satellite and/or by comparing code and carrier measurements (Lau and Cross, Reference Lau and Cross2007). However, this does not mitigate NLOS reception as the measurements from the same satellite are affected equally.
Multi-constellation GNSS provides the user with a much greater choice of signals. Accuracy can thus be maximised by selecting only those signals least contaminated by multipath and NLOS propagation to form the navigation solution and discarding the rest. There is limited scope to do this with single-constellation GNSS.
Most NLOS signals can be detected using the dual-polarisation technique (Jiang and Groves, 2012b). This separately correlates the right hand circularly polarized (RHCP) and left hand circularly polarized (LHCP) outputs of a dual-polarization antenna and differences the resulting C/N 0 measurements, producing a result that is positive for directly received signals and negative for most NLOS signals. In principle, the method could also be used to detect severe multipath interference. However, this requires either more sophisticated antenna calibration or a more regular LHCP gain pattern.
Other hardware-based approaches include detecting NLOS signals using a panoramic camera (Marais et al., Reference Marais, Berbineau and Heddebaut2005; Meguro et al., Reference Meguro, Murata, Takiguchi, Amano and Hashizume2009) and using an antenna array to detect both NLOS reception and multipath interference (Keshavadi et al., Reference Keshvadi, Broumandan and Lachapelle2011). NLOS prediction using a 3D city model has also been demonstrated for cases where the user position is already known (Obst et al., Reference Obst, Bauer and Wanielik2012; Peyraud et al., Reference Peyraud, Bétaille, Renault, Ortiz, Mougel, Meizel and Peyret2013).
This paper assesses techniques that do not require additional hardware. Signal selection by consistency checking is based on the principle that NLOS and multipath-contaminated measurements produce a less consistent navigation solution than “clean” direct line-of-sight (LOS) measurements. In other words, if position solutions are computed using combinations of signals from different satellites, those obtained using only the multipath-free signals should be in greater agreement than those that include multipath-contaminated and NLOS measurements. Thus these measurements may be identified through various consistency-checking based approaches. By eliminating these contaminated measurements, a more accurate position solution can potentially be obtained. The same principle is used for fault detection in receiver autonomous integrity monitoring (RAIM) (Feng et al., Reference Feng, Ochieng, Walsh and Ioannides2006). The difference is that the purpose of RAIM is to detect and exclude faulty data and to calculate protection levels, whereas here, the aim is to identify the set of measurements least affected by multipath and NLOS propagation.
Previous work (Jiang et al., Reference Jiang, Groves, Ochieng, Feng, Milner and Mattos2011) has shown that a conventional sequential testing approach to consistency checking can successfully eliminate NLOS and multipath-contaminated signals in environments where the majority of signals are received by direct line of sight with little multipath contamination. However, in dense urban environments with multiple NLOS and multipath-contaminated signals, the sequential testing approach is prone to eliminating the wrong signals. Performance is improved by weighting the position solution according to the C/N 0 level on the basis that NLOS signals and some, but not all, multipath-contaminated signals are generally weaker than “clean” direct-LOS signals. However, further tests (Jiang and Groves, Reference Jiang and Groves2012a) have shown that even with C/N 0-weighting, the sequential testing method can still eliminate the wrong signals in dense urban areas, degrading the positioning performance.
Therefore, a new consistency checking method, based on subset comparison has been developed. This identifies the most self-consistent set of signals, retaining the C/N 0-based weighting, and then uses them to calculate the position solution. Subset comparison is thus a “bottom up” approach, in contrast to the “top down” approach of the sequential testing method. A “bottom up” approach has also recently been proposed for RAIM (Feng et al., Reference Feng, Jokinen, Ochieng and Milner2012). Initial tests have shown that the subset comparison method performs significantly more reliably in urban areas than the sequential testing approach (Jiang and Groves, Reference Jiang and Groves2012a). However, there are still cases where it selects a sub-optimal set of signals, particularly where there are insufficient direct LOS signals uncontaminated by multipath interference.
This paper presents extensive test results of both consistency checking methods and C/N 0-based weighting, and introduces height aiding. Terrain height can be obtained from a 3D city model or a separate terrain height database and is typically more reliable than the GNSS measurements in urban environments. A recent height solution from a nearby location with good GNSS reception may also be suitable. Iwase et al. (Reference Iwase, Suzuki and Watanabe2013) used terrain height from a database to validate a set of signals. Here, the terrain height is used to generate a virtual ranging measurement (Amt and Raquet, Reference Amt and Raquet2006) which is used in both the position solution and the subset comparison consistency checking method. In the latter, it is included in all of the measurement subsets in order to improve the reliability of the consistency checking.
Section 2 describes the least-squares position solution with the different weighting schemes. Sections 3 and 4 respectively summarise the sequential testing and subset comparison consistency-checking methods. Section 5 then describes how height aiding is used to enhance the subset comparison method. Section 6 presents test results obtained using two GPS/GLONASS data sets, each collected from multiple sites in different parts of Central London. Position solutions with and without height aiding, C/N 0-based weighting and both consistency-checking methods are compared. Finally, Section 7 summarises the conclusions and discusses topics for future research.
2. LEAST-SQUARES POSITIONING
A position solution may be computed from a set of pseudo-range measurements using least-squares estimation. This is given by (Groves, Reference Groves2013)
where ![]() ${\bf \hat x}^ + $ is the estimated state vector, comprising the position and time solution,
${\bf \hat x}^ + $ is the estimated state vector, comprising the position and time solution, ![]() ${\bf \hat x}^ - $ is the predicted state vector,
${\bf \hat x}^ - $ is the predicted state vector, ![]() ${\bf \tilde z}$ is the measurement vector,
${\bf \tilde z}$ is the measurement vector, ![]() ${\bf \hat z}^ - $ is the vector of measurement predictions from
${\bf \hat z}^ - $ is the vector of measurement predictions from ![]() ${\bf \hat x}^ - $, Wρ is the weighting matrix and HGe is the measurement matrix.
${\bf \hat x}^ - $, Wρ is the weighting matrix and HGe is the measurement matrix.
For GPS and GLONASS measurements with an unknown interconstellation timing offset, the state vector and measurement vector are
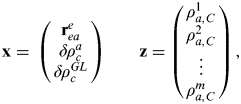 $${\bf x} = \matrix{ {\left( {\matrix{ {{\bf r}_{ea}^e} \cr {\delta \rho _c^a} \cr {\delta \rho _c^{GL}} \cr}} \right)} & {\quad {\bf z} = \left( {\matrix{ {\rho _{a,C}^1} \cr {\rho _{a,C}^2} \cr \vdots \cr {\rho _{a,C}^m} \cr}} \right)} \cr}, $$
$${\bf x} = \matrix{ {\left( {\matrix{ {{\bf r}_{ea}^e} \cr {\delta \rho _c^a} \cr {\delta \rho _c^{GL}} \cr}} \right)} & {\quad {\bf z} = \left( {\matrix{ {\rho _{a,C}^1} \cr {\rho _{a,C}^2} \cr \vdots \cr {\rho _{a,C}^m} \cr}} \right)} \cr}, $$where reae is the Cartesian position, resolved about and with respect to an Earth-centred Earth-fixed (ECEF) frame, δρ ca and δρ cGL are, respectively, the receiver clock offset and GLONASS-GPS timing offset, expressed as ranges, ρ a,Cj is the pseudo-range from satellite j and m is the number of satellite used. The measurement matrix is given by
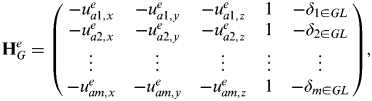 $${\bf H}_G^e = \left( {\matrix{ { - u_{a1,x}^e} & { - u_{a1,y}^e} & { - u_{a1,z}^e} & 1 & { - \delta _{1 \in GL}} \cr { - u_{a2,x}^e} & { - u_{a2,y}^e} & { - u_{a2,z}^e} & 1 & { - \delta _{2 \in GL}} \cr \vdots & \vdots & \vdots & \vdots & \vdots \cr { - u_{am,x}^e} & { - u_{am,y}^e} & { - u_{am,z}^e} & 1 & { - \delta _{m \in GL}} \cr}} \right),$$
$${\bf H}_G^e = \left( {\matrix{ { - u_{a1,x}^e} & { - u_{a1,y}^e} & { - u_{a1,z}^e} & 1 & { - \delta _{1 \in GL}} \cr { - u_{a2,x}^e} & { - u_{a2,y}^e} & { - u_{a2,z}^e} & 1 & { - \delta _{2 \in GL}} \cr \vdots & \vdots & \vdots & \vdots & \vdots \cr { - u_{am,x}^e} & { - u_{am,y}^e} & { - u_{am,z}^e} & 1 & { - \delta _{m \in GL}} \cr}} \right),$$where uaje is the line-of-sight vector from the user antenna to satellite j and δ j∈GL is 1 where satellite j is a GLONASS satellite and zero otherwise. The line-of-sight vectors and predicted pseudo-ranges, ![]() $\hat \rho _{a,C}^{\,j -} $, are given by
$\hat \rho _{a,C}^{\,j -} $, are given by
 $${\bf u}_{aj}^e \approx \displaystyle{{{\bf \hat r}_{ej}^e - {\bf \hat r}_{ea}^{e -}} \over {\left| {{\bf \hat r}_{ej}^e - {\bf \hat r}_{ea}^{e -}} \right|}},$$
$${\bf u}_{aj}^e \approx \displaystyle{{{\bf \hat r}_{ej}^e - {\bf \hat r}_{ea}^{e -}} \over {\left| {{\bf \hat r}_{ej}^e - {\bf \hat r}_{ea}^{e -}} \right|}},$$where ![]() ${\bf \hat r}_{ej}^e $ is the position of satellite j,
${\bf \hat r}_{ej}^e $ is the position of satellite j, ![]() ${\bf \hat r}_{ea}^{e -} $ is the predicted user position,
${\bf \hat r}_{ea}^{e -} $ is the predicted user position, ![]() $\delta \hat \rho _c^{a -} $ is the predicted receiver clock offset,
$\delta \hat \rho _c^{a -} $ is the predicted receiver clock offset, ![]() $\delta \hat \rho _c^{GL -} $ is the predicted GLONASS-GPS timing offset,
$\delta \hat \rho _c^{GL -} $ is the predicted GLONASS-GPS timing offset, ![]() $\delta \hat \rho _{ie,a}^{\,j -} $ is the satellite j Sagnac correction and δ j∈GL is 1 for GLONASS satellites and 0 otherwise (Groves, Reference Groves2013).
$\delta \hat \rho _{ie,a}^{\,j -} $ is the satellite j Sagnac correction and δ j∈GL is 1 for GLONASS satellites and 0 otherwise (Groves, Reference Groves2013).
Three different weighting schemes are considered: conventional elevation-based weighting, C/N 0-based weighting and no weighting. Without weighting, Wρ is simply the identity matrix. Otherwise,
 $${\bf W}_\rho = \left( {\matrix{ {\sigma _{\rho 1}^{ - 2}} & 0 & \cdots & 0 \cr 0 & {\sigma _{\rho 2}^{ - 2}} & \cdots & 0 \cr \vdots & \vdots & \ddots & \vdots \cr 0 & 0 & \cdots & {\sigma _{\rho m}^{ - 2}} \cr}} \right),$$
$${\bf W}_\rho = \left( {\matrix{ {\sigma _{\rho 1}^{ - 2}} & 0 & \cdots & 0 \cr 0 & {\sigma _{\rho 2}^{ - 2}} & \cdots & 0 \cr \vdots & \vdots & \ddots & \vdots \cr 0 & 0 & \cdots & {\sigma _{\rho m}^{ - 2}} \cr}} \right),$$where, for elevation-based weighting,
where θ nuaj is the elevation angle of the j th satellite and the constants are a=0·13 m, b=0·56 m and θ 0=0·1745 rad (RTCA, 2006), while, for C/N 0-based weighting,
where (C/N 0)j is the measured carrier-power-to-noise-density ratio of the j th satellite signal in dB-Hz and c=1·1×104 m2 is a constant (Hartinger and Brunner, Reference Hartinger and Brunner1999).
3. SEQUENTIAL TESTING CONSISTENCY-CHECKING METHOD
The first stage of the sequential testing consistency-checking method is to compute a position solution using pseudo-range measurements from all of the satellites tracked as described in the preceding section. A vector of residuals is then calculated using
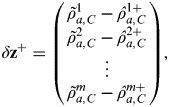 $$\delta {\bf z}^ + = \left( {\matrix{ {\tilde \rho _{a,C}^1 - \hat \rho _{a,C}^{1 +}} \cr {\tilde \rho _{a,C}^2 - \hat \rho _{a,C}^{2 +}} \cr \vdots \cr {\tilde \rho _{a,C}^m - \hat \rho _{a,C}^{m +}} \cr}} \right),$$
$$\delta {\bf z}^ + = \left( {\matrix{ {\tilde \rho _{a,C}^1 - \hat \rho _{a,C}^{1 +}} \cr {\tilde \rho _{a,C}^2 - \hat \rho _{a,C}^{2 +}} \cr \vdots \cr {\tilde \rho _{a,C}^m - \hat \rho _{a,C}^{m +}} \cr}} \right),$$where ![]() $\hat \rho _{a,C}^{\, j +} $ is the pseudo-range to satellite j estimated from the position and timing solution,
$\hat \rho _{a,C}^{\, j +} $ is the pseudo-range to satellite j estimated from the position and timing solution, ![]() ${\bf \hat x}^ + $. A test statistic based on the sum of the squares of the residuals,
${\bf \hat x}^ + $. A test statistic based on the sum of the squares of the residuals, ![]() ${\delta {\bf z}^ +} ^{\rm T} \delta {\bf z}^ + $, is then compared with a threshold derived from a chi-square distribution (Jiang et al., Reference Jiang, Groves, Ochieng, Feng, Milner and Mattos2011; Feng et al., Reference Feng, Ochieng, Walsh and Ioannides2006). Where the test statistic falls within the threshold, the position solution is accepted. Otherwise, it is assumed that at least one measurement is NLOS, multipath-contaminated or subject to another source of error. The measurement with the largest residual is then eliminated as it is least consistent with the others and the process repeats.
${\delta {\bf z}^ +} ^{\rm T} \delta {\bf z}^ + $, is then compared with a threshold derived from a chi-square distribution (Jiang et al., Reference Jiang, Groves, Ochieng, Feng, Milner and Mattos2011; Feng et al., Reference Feng, Ochieng, Walsh and Ioannides2006). Where the test statistic falls within the threshold, the position solution is accepted. Otherwise, it is assumed that at least one measurement is NLOS, multipath-contaminated or subject to another source of error. The measurement with the largest residual is then eliminated as it is least consistent with the others and the process repeats.
As Figure 1 shows, this process continues until either a test statistic is obtained that falls within the threshold or the number of measurements remaining is the minimum needed to compute the position and clock solution. As measurements are sequentially removed from the position solution until one of these criteria is met, this may be thought of as a “top down” approach.

Figure 1. The sequential testing approach to consistency checking.
This sequential testing approach is well established for RAIM. However, for detecting NLOS reception and multipath interference, there are some problems with the underlying assumptions. Firstly, the measurement errors are assumed to follow a zero-mean Gaussian distribution; hence the use of a chi-square hypothesis test to examine the normality of the measurement residuals. However, the pseudo-range errors due to NLOS signals reception are always positive, so their distribution is clearly not Gaussian.
The second assumption is that the errors on different signals are mutually independent. However, in dense urban areas, a set of received signals may be found that are consistent among themselves, but still produce an erroneous position solution. One cause of this is reception of multiple signals reflected off the same surface.
The final assumption is that the contaminated signals are the minority among those received. However, in dense urban environments, the majority of signals may be NLOS or affected by severe multipath interference. In such cases, the residuals produced from a weighted least-squares solution can be poor indicators of the quality of the individual signals. This is because the least-squares estimation method performs poorly on data sets containing a high proportion of outliers (Torr and Zisserman, Reference Torr and Zisserman2000). A more flexible approach to consistency checking is therefore needed for identifying and excluding NLOS and multipath-contaminated signals.
4. SUBSET COMPARISON CONSISTENCY-CHECKING METHOD
The aim of consistency checking is to identify the subset of GNSS measurements that are most consistent with each other on the basis that these are least likely to be contaminated by NLOS reception and severe multipath interference. The subset comparison method works by scoring different subsets of the GNSS measurements according to their consistency and then using the most consistent subset to form the position solution.
The basis of this method is the minimal sample set (MSS), a subset consisting only of the minimum number of measurements required to produce an exact solution. Each MSS is used to predict the remaining pseudo-ranges, which are compared with their measured values, both to score the MSS and to identify which of the measurements are consistent with it. Different criteria may be used for this, enabling the method to be adapted to different statistical distributions of the NLOS and multipath errors.
The subset comparison method thus builds the final subset from the bottom up, as opposed to from the top down as in the case of the sequential testing method. While sequential testing compares one set of measurements against a threshold to determine whether to accept it or try a smaller set, subset comparison compares a variety of subsets against each other in order to find the most consistent. By considering more options it is thus more likely to find the optimum subset.
It is not necessary to compute and test every possible MSS. This is because the objective is to obtain the final measurement subset, which may be built up from a number of different MSSs. For example, a 7-measurement final subset incorporates 21 different 5-measurement subsets. The algorithm presented here is based on a technique known as random sample consensus (RANSAC), which uses random-draw subsets of the measurements and a probability-based stopping criterion for efficiency. The RANSAC technique was previously proposed for computer image processing to deal with data sets with high proportions of outliers (Torr and Zisserman, Reference Torr and Zisserman2000).
Figure 2 shows the consistency checking process using the RANSAC-based subset comparison method. First of all, a minimal sample set is randomly selected from all the measurements available at one epoch. Where the GLONASS-GPS timing offset is estimated, each MSS comprises measurements from five satellites, which must include at least one GPS measurement and at least one GLONASS. Otherwise, it is not possible to form predictions of all of the remaining measurements.

Figure 2. The subset comparison approach to consistency checking.
The MSS is then assessed, resulting in a consensus set (CS), which is the set of other measurements that are found to be consistent with the MSS, and a cost function, which is a measure of the consistency. The process is iterated to find a MSS that generates the minimum cost function. This continues until there have been sufficient iterations for the probability of finding a better MSS to fall below a certain threshold. Details are presented below.
Consider the i th MSS, comprising the measurements ![]() ${\bf \tilde z}^i \in {\bf \tilde z}$. Once the MSS has been generated, an exact position and time solution,
${\bf \tilde z}^i \in {\bf \tilde z}$. Once the MSS has been generated, an exact position and time solution, ![]() ${\bf \hat x}^{ + i} $, may be obtained using least-squares estimation (Groves, Reference Groves2013)
${\bf \hat x}^{ + i} $, may be obtained using least-squares estimation (Groves, Reference Groves2013)
where HGe,i comprises the rows of the measurement matrix, HGe, given by (3), which correspond to the i th MSS, ![]() ${\bf \hat z}^{i -} $ comprises the elements of the predicted measurement vector,
${\bf \hat z}^{i -} $ comprises the elements of the predicted measurement vector, ![]() ${\bf \hat z}^ - $, given by (2), corresponding to the i th MSS and
${\bf \hat z}^ - $, given by (2), corresponding to the i th MSS and ![]() ${\bf \hat x}^ - $ is the predicted state vector, also defined by (2).
${\bf \hat x}^ - $ is the predicted state vector, also defined by (2).
A set of “residuals” for this MSS, ei, is then calculated using
where ![]() ${\bf \hat z}^{ + i} $ is the set of measurements predicted from the i th MSS position and time solution,
${\bf \hat z}^{ + i} $ is the set of measurements predicted from the i th MSS position and time solution, ![]() ${\bf \hat x}^{ + i} $ (Groves, Reference Groves2013). The components of ei corresponding to the i th MSS are zero so need not be calculated explicitly. These “residuals” are then used to determine the consensus set and the cost function.
${\bf \hat x}^{ + i} $ (Groves, Reference Groves2013). The components of ei corresponding to the i th MSS are zero so need not be calculated explicitly. These “residuals” are then used to determine the consensus set and the cost function.
The CS is determined by comparing the magnitudes of the “residuals” of all measurements outside the MSS with a threshold, δ. For the results presented here, δ was determined empirically, with a value of 12·5 m found to give the best results. If a “residual” falls within the threshold, the measurement it corresponds to is considered consistent with the MSS position and time solution and is thus included in the consensus set for that MSS. Otherwise, the measurement is deemed to be an outlier and is excluded from the CS.
The cost function, Ci, used to measure the quality of the i th MSS and its associated CS may take various forms. A common RANSAC cost function, based purely on the size of individual “residual” and assuming a Gaussian distribution, is defined by (Torr and Zisserman, Reference Torr and Zisserman2000) as
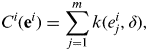 $$C^i ({\bf e}^i ) = \sum\limits_{\,j = 1}^m {k(e_j^i, \delta )}, $$
$$C^i ({\bf e}^i ) = \sum\limits_{\,j = 1}^m {k(e_j^i, \delta )}, $$where
where σ ρj is given by (7) or (8). Weighting is applied to the cost function because selecting measurements based on both consistency and C/N 0 was found to give better performance than using consistency alone (Jiang et al., Reference Jiang, Groves, Ochieng, Feng, Milner and Mattos2011). Considering the C/N 0-based weighting, the cost function is higher when the C/N 0 levels of the measurements outside the MSS are lower. Thus, an MSS that comprises measurements with higher C/N 0 levels will typically have a lower cost function, making it more likely to be selected.
Once calculated, the cost function is compared with the previous minimum. If it is lower, the MSS and CS are provisionally selected as the final subset of measurements for calculating the output position and timing solution. The preceding process is then repeated with a new MSS until the number of iterations reaches a certain threshold.
Under the hypothesis that no measurements are contaminated, let q be the probability of sampling a MSS for which all of the remaining measurements are accepted into the CS. The probability of picking a MSS for which there is at least one outlier is thus 1−q. The probability of constructing h MSSs and all of them leading to the detection of outliers is therefore (1−q)h. h should be sufficiently large that (1−q)h<α, where α is the false alarm probability. This can be rewritten as:
where ⌈x⌉ denotes the smallest integer larger than x. Therefore, with a given false alarm rate, α, the iterative part of the RANSAC algorithm should stop when the number of MSSs generated reaches T.
Assuming that each set of measurements has the same probability of being selected, q is estimated to be (Torr and Zisserman, Reference Torr and Zisserman2000)
where ![]() $\left( {\matrix{ a \cr b \cr}} \right)$ is the number of b-element combinations of a set of size a, n M is the size of the MSS, n C is the number of measurements in the current best CS, and m is the total number of measurements as before. Thus, each time a new MSS and CS is found, q, and hence T, are updated.
$\left( {\matrix{ a \cr b \cr}} \right)$ is the number of b-element combinations of a set of size a, n M is the size of the MSS, n C is the number of measurements in the current best CS, and m is the total number of measurements as before. Thus, each time a new MSS and CS is found, q, and hence T, are updated.
Once a best MSS and its CS have been identified as the final measurement set through their cost function, they are used with an appropriate weighting scheme to produce a new least-squares position solution. Thus, from Section 2,
where HGe,f comprises the rows of the measurement matrix, HGe, given by (3), which corresponds to the final set of measurements, ![]() ${\bf \tilde z}^f $ is the final set of measurements,
${\bf \tilde z}^f $ is the final set of measurements, ![]() ${\bf \hat z}^{\,f -} $ comprises the elements of the predicted measurement vector,
${\bf \hat z}^{\,f -} $ comprises the elements of the predicted measurement vector, ![]() ${\bf \hat z}^ - $, given by (2), corresponding to the final set and Wρf comprises the corresponding rows and columns of the weighting matrix, Wρ, given by (6).
${\bf \hat z}^ - $, given by (2), corresponding to the final set and Wρf comprises the corresponding rows and columns of the weighting matrix, Wρ, given by (6).
In cases where the MSS with the lowest cost function has fewer than one measurement in its consensus set, it is not possible to confirm that this measurement subset (or any other) is self-consistent, so consistency checking is deemed to have failed and the all-satellite position solution is used.
5. HEIGHT AIDING
The height obtained from a 3D city model or a separate terrain height database may be used to calculate an additional ranging measurement from a virtual transmitter at the centre of the Earth (Amt and Raquet, Reference Amt and Raquet2006). Where the GNSS signal geometry is good, height aiding only improves the vertical position solution (and the receiver clock offset estimate). However, in cases where the geometry is poor, such as the side of an urban street, horizontal positioning can also be improved.
The height-aiding measurement forms the m+1th component of the measurement vector, z. However, where this height is also used to calculate the predicted position, ![]() ${\bf \hat r}_{ea}^{e -} $, the height measurement innovation will be zero, i.e.
${\bf \hat r}_{ea}^{e -} $, the height measurement innovation will be zero, i.e. ![]() $\hat z_{m + 1}^ - = \tilde z_{m + 1} $. The additional row of the measurement matrix is
$\hat z_{m + 1}^ - = \tilde z_{m + 1} $. The additional row of the measurement matrix is
where ueae is the unit vector describing the direction from the centre of the Earth to the predicted user position, given by
Note that the columns of (17) corresponding to the clock offset and interconstellation timing bias are both zero. The variance of the height-aiding measurement, forming the m+1th diagonal element of Cρ, was assumed to be (5 m)2 for the results presented here.
Height aiding also provides valuable additional information for consistency checking. With an additional measurement that is more reliable than the GNSS measurements, it should be easier to spot outliers.
For the subset comparison method, every MSS comprises four GNSS measurements plus the height-aiding measurement instead of 5 GNSS measurements. Other changes are that two or more measurements are required to be in the consensus set for a measurement subset to be considered self-consistent and the threshold for accepting measurements into the consensus set, δ, is 2·5 m. These values were determined empirically to give the best results. Thus, a subset solution is only selected in preference to the all-signal solution when a highly consistent subset is available. Otherwise, the consistency checking proceeds as described in Section 3.
A version of the subset comparison method with five GNSS measurements and the height-aiding measurement in each MSS has also been tested and gives similar average performance. An alternative approach which is still to be tested is to incorporate the difference between the database-indicated height and the MSS height solutions in the cost function. This is similar to the method proposed by Iwase et al. (Reference Iwase, Suzuki and Watanabe2013).
6. EXPERIMENTAL TESTING
Experimental data was collected on two separate days across multiple test sites in Central London using Leica Viva GS15 multi-constellation geodetic-grade GNSS user equipment. The polarisation discrimination of the antenna and the design of the correlators and discriminators within the receiver already reduce the impact of multipath interference significantly. They have little direct impact on the ranging errors due to NLOS reception. However, the attenuation of most reflected signals by the antenna does make NLOS easier to detect through C/N 0.
L1 pseudo-range measurements from all available GPS and GLONASS satellites were used to calculate position solutions using different combinations of the measurement weighting schemes, the two consistency checking methods and height aiding. Ionosphere propagation delay corrections were applied using the Klobuchar model (GPS Directorate, 2011) and troposphere delay corrections using the initial Wide Area Augmentation System (WAAS) model (Collins, Reference Collins1999) to give results representative of consumer-grade user equipment.
Height-aiding measurements were simulated by taking the true height and adding a different random error at each epoch taken from a zero-mean Gaussian distribution with a standard deviation of 5 m, chosen to represent the expected accuracy of height-aiding measurements. The main cause of the height aiding error is the difference in height between the true user position and the position used to obtain the height from the database. If the latter is taken from the all-satellite GNSS position solution it will typically have an error of several tens of metres, resulting in an error of a few metres in the height measurement. Other error sources include errors in the database itself, variations in the terrain height due to solid Earth tides and variations in the user height above ground.
The first set of test data was collected near Moorgate underground station on 8 April 2011. There are three sites within the test data set, each occupied for about 38 minutes. Figure 3 shows an overview of the test sites. The truth was established using traditional surveying methods and is accurate at the cm-level.

Figure 3. Locations of the Test Set 1 sites (Background Image © 2013 Bluesky © Google).
The second test data set was collected near Fenchurch Street station on 23 July 2012. Overall 22 sites were occupied to cover a variety of road conditions. Each site was occupied for two periods of about 10 minutes approximately 3 hours apart. Figure 4 depicts an overview of the test sites. The truth was established to decimetre-level accuracy using a 3D city model with tape measurements from landmarks.

Figure 4. Locations of the Test Set 2 sites (Background Image © 2013 Bluesky © Google).
The performance obtained from the two sets of data was very similar, so the results are combined. Tables 1, 2 and 3 show, respectively, the root mean square (RMS) positioning error, percentage of positioning errors greater than 50 m and percentage of positioning errors greater than 25 m horizontally and vertically.
Table 1. Horizontal and vertical RMS position errors.
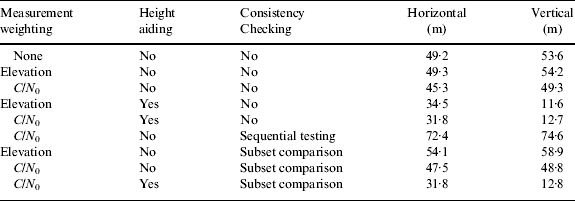
Table 2. Percentage of position errors greater than 50 m.

Table 3. Percentage of position errors greater than 25 m.
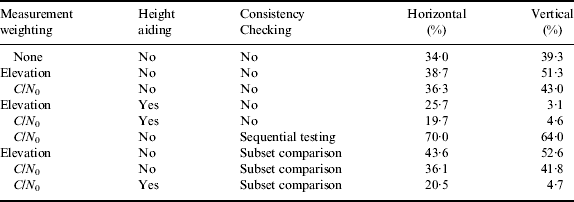
Considering the measurement weighting schemes first, it is clear that, compared to no weighting, elevation-based weighting has negligible impact on the RMS position error and the number of outliers greater than 50 m, while increasing the number of outliers between 25 m and 50 m. This was unexpected and suggests that the commonly held assumption that low-elevation GNSS measurements are more likely to be NLOS or multipath-contaminated than higher elevation signals may not hold in dense urban environments. C/N 0-based weighting improves the RMS accuracy and reduces the number of outliers greater than 50 m, but increases the number of outliers between 25 m and 50 m. Thus, overall, C/N 0-based weighting gives slightly better performance, which is to be expected as NLOS signals are normally weaker than those received directly.
Comparing the results with and without height aiding, it can be seen that the height aiding makes a substantial difference to the performance, reducing the RMS errors and the number of outliers. Horizontal positioning is improved as well as vertical due to the better geometry.
Moving on to the consistency checking results without height aiding, it can be seen that using sequential testing actually makes the positioning performance worse in this environment, confirming what has been observed previously (Jiang et al., Reference Jiang, Groves, Ochieng, Feng, Milner and Mattos2011; Jiang and Groves, Reference Jiang and Groves2012a). If measurements are effectively excluded from the position solution at random, then a poorer performance would be expected on average simply because fewer measurements are contributing to the position solution so the geometry is poorer.
Consistency checking using subset comparison has very little effect on the average positioning performance, either with or without height aiding. However, it produces more accurate position solutions in some cases and degrades performance in others. Thus, sometimes consistency checking works as intended, whereas at other times, random measurements are eliminated, degrading the signal geometry. Poor performance can be attributed to a lack of good signals. At least six measurements are required to demonstrate consistency (one more than the number of states estimated). However, measurements were typically only obtained from eight or nine satellites, so in many cases, there would have been fewer than six direct LOS signals without significant multipath.
By way of example, Figure 5 compares the position errors obtained at Site T3 in test set 1 using a combination of C/N 0-based measurement weighting, height aiding and consistency checking using subset comparison with those obtained using conventional elevation-based weighting without height aiding or consistency checking. Overall, the combined approach produces a more accurate position solution, particularly in the vertical axis, as might be expected with height aiding. The new method eliminates many of the outliers and reduces the size of many others. However, some outliers remain, while additional outliers are introduced around 1, 23·5 and 26·5 minutes. Figure 6 displays the corresponding horizontal position solutions at 1-second intervals.

Figure 5. Position errors for site T3 from Test Set 1. Red denotes conventional elevation-based weighting without height aiding or consistency checking. Green denotes a combination of C/N 0-based measurement weighting, height aiding and consistency checking using subset comparison.

Figure 6. Position solutions for site T3 from Test Set 1. Red diamonds denote conventional elevation-based weighting without height aiding or consistency checking. Green triangles denote a combination of C/N 0-based measurement weighting, height aiding and consistency checking using subset comparison. The yellow pin in each picture indicates the true position and the circles mark position errors of 25 m and 50 m.
7. CONCLUSIONS AND RECOMMENDATIONS
The ability of C/N 0 weighting, height aiding and consistency checking to improve GNSS positioning in dense urban areas, separately and in combination, has been assessed using data collected at multiple sites. On its own, C/N 0 weighting brings a small improvement to the overall positioning accuracy and reduces the number of the largest outliers. Using a height aiding measurement from a 3D city model or separate terrain height database significantly improves positioning accuracy, horizontally as well as vertically, due to the improved solution geometry.
Consistency checking using the conventional “top down” sequential testing approach was found to make performance worse in dense urban areas, so its use cannot be recommended. The new “bottom up” subset comparison consistency-checking method was found to improve performance at some test sites, but not others; the overall impact was neutral.
The subset comparison method has considerable potential for further development. Performance may improve as the number of GNSS satellites increases and broadcast interconstellation timing offsets become widely available, removing the need to estimate them. There is scope to improve the cost function and consensus set selection criteria, for example, by considering the signal geometry. It should also be possible to make a more intelligent measurement selection by comparing the cost functions of all of the minimum sample sets instead of automatically selecting the MSS and CS with the lowest cost function. Consistency checking could also be used to re-weight measurements within the position solution as well as eliminating them. Finally, testing is needed over a wider range of environments. Thus, further research is needed before the subset comparison approach to consistency-checking can be either recommended or rejected.
Other topics for further research include NLOS prediction using a 3D city model, when the user position is only approximately known, as discussed in (Groves et al., Reference Groves, Jiang, Wang and Ziebart2012) and the generation of an intelligent urban positioning solution by combining augmented conventional positioning with the shadow-matching technique (Groves, Reference Groves2011; Wang et al., Reference Wang, Groves and Ziebart2012).
ACKNOWLEDGEMENTS
This work is part of the Innovative Navigation using new GNSS Signals with Hybridised Technologies (INSIGHT) program. INSIGHT (www.insight-gnss.org) is a collaborative research project funded by the UK's Engineering and Physical Sciences Research Council (EPSRC) to extend the applications and improve the efficiency of positioning through the exploitation of new global navigation satellite systems signals. It is being undertaken by a consortium of twelve UK university and industrial groups: Imperial College London, University College London, the University of Nottingham, the University of Westminster, EADS Astrium, Nottingham Scientific Ltd, Leica Geosystems, Ordnance Survey of Great Britain, QinetiQ, STMicroelectronics, Thales Research and Technology UK Limited, and the UK Civil Aviation Authority.
The authors would like to thank Chris Atkins, Chian-yuan Naomi Li, Lei Wang and Toby Webb for assisting with the experimental work. The use of functions from GPS Toolkit (Tolman et al., Reference Tolman, Harris, Gaussiran, Munton, Little, Mach, Nelsen, Renfro and Schlossberg2004) is also acknowledged.











