Thomas Hariot's recently discovered manuscript ‘The Doctrine of Nauticall Triangles Compendious’ was the subject of a paper in this Journal by Professor Taylor and D. H. Sadler which poses but leaves unanswered the intriguing question of the method he employed in his computation. Sadler shows that the method depends on the fact that if sequences of meridional parts are in arithmetic progression the corresponding values of tan (45° − ½φ) will be in geometric progression. This is at once obvious from the modern formula for meridional parts:

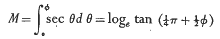
But how did Hariot, writing before 1596, discover the relationship when neither logarithms nor the integral calculus had yet been invented; and was he able to prove it? It is the purpose of the present paper to supply a proof which requires neither logarithms nor the calculus. It is not claimed that this was necessarily the method that Hariot employed, although the manuscript reveals several points of similarity.