1. INTRODUCTION
Global Navigation Satellite Systems (GNSS) Precise Point Positioning (PPP) technique has been an active research topic over the past 15 years. This mode of positioning conforms to the original intention of Global Positioning System (GPS) or GNSS usage that is single receiver positioning. The PPP technique is capable of providing positioning solutions at centimetre- to decimetre-level anywhere, without the need of having one or more nearby ground GNSS reference stations for simultaneous observations. It only requires a sparse network of ground reference stations distributed globally to generate precise satellite orbit and clock corrections necessary for PPP, which makes this mode of positioning comparatively cost effective and operationally flexible. The distinction between PPP and the well-established differential positioning technique, e.g., Real-Time Kinematic (RTK) is that, instead of using ground stations as reference points, PPP makes use of precise information of the satellite orbits, clocks and robust error modelling to derive accurate estimates of the user's receiver position (Kouba, Reference Kouba2009; Kouba and Hèroux, Reference Kouba and Hèroux2001; Zumberge et al., Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997). The PPP technique is especially useful for positioning and navigation in remote regions where ground-based GNSS reference station infrastructure is sparse or unavailable (Bisnath and Collins, Reference Bisnath and Collins2012). Additionally, the errors affecting GNSS such as the satellite orbits and clocks, are better modelled and represented in PPP through an approach known as state-space modelling or State-Space Representation (SSR) (Wübbena et al., Reference Wübbena, Schmitz and Andreas2005). Instead of lumping all error components together as one error as is the case in the conventional differential technique, SSR errors are better modelled and transmitted individually. This leads to improved performance as bandwidth can be optimised based on the spatial and temporal characteristics of the errors. SSR is ideal for broadcasting of corrections to a large number of users over a wide area.
The caveats of PPP are the availability of precise satellite orbit and clock corrections, and communication channels used to disseminate these corrections. The corrections need to be transmitted to PPP users and this is especially critical for real-time applications, which makes real-time PPP far more challenging than using post-processing mode. In April 2013, the International GNSS Service (IGS) launched a public Real-Time Service (RTS) to support real-time high precision GNSS applications requiring access to high accuracy but with low latency corrections (IGS, 2013). The IGS-RTS is at present a GPS-only service and GLONASS corrections are offered as an experimental product. The IGS real-time products can be streamed for free via the Internet. There are also a number of commercial services offered by private companies providing similar corrections either via terrestrial communication links such as mobile Internet and/or space-based means such as geostationary satellites. From a practical viewpoint, using space-based satellite means is an ideal communication link for PPP as the SSR corrections are globally valid and transmissions can be received by a large number of users.
The Quasi-Zenith Satellite System (QZSS) is a Japanese satellite navigation system developed by Japan Aerospace Exploration Agency (JAXA). The objective of QZSS is to enhance the current availability and performance of GNSS typically over Japan and neighbouring Asia Oceania countries. Besides transmitting conventional positioning signals, QZSS also transmits augmentation signals to enhance the performance of GNSS (JAXA, 2013; Nishiguchi, Reference Nishiguchi2010). One of the QZSS augmentation signals is the L-band experimental (LEX) signal. This signal is designed to enable high accuracy positioning in real-time and time transfers through transmission of precise corrections. RTK-like performance (3 cm horizontal and 6 cm vertical RMS errors with time to first fix of 35 seconds) has been reported in Japan utilising regional corrections that are only valid in Japan and also include atmospheric corrections (Saito et al., Reference Saito, Sato, Miya, Shima, Omura, Takiguchi and Asari2011). Another type of correction messages transmitted on the LEX signal has wide-area validity and is currently in testing phase for high accuracy point positioning. These messages are known as ‘MADOCA-LEX’ (Multi-GNSS Advanced Demonstration of Orbit and Clock Analysis) messages.
In this study, we present an analysis of the quality of the current satellite orbit and clock corrections broadcast on the LEX signal. The aim is to evaluate the capability of the QZSS LEX signal and messages to deliver high accuracy real-time PPP solutions in both static and kinematic modes. The theoretical aspect of PPP including the functional model is assumed known and hence will not be discussed. Interested readers are recommended to refer to Kouba (Reference Kouba2009), Kouba and Heroux (Reference Kouba and Hèroux2001) and Zumberge et al. (Reference Zumberge, Heflin, Jefferson, Watkins and Webb1997).
This paper is comprised of five sections. First, a description of the Japanese QZSS system is given in Section 2. The structure of the LEX signal and messages are presented in Section 3. Section 4 describes the quality of the orbit and clock corrections transmitted on the LEX signal. Then the positioning results of the real-time PPP processing using the LEX correction messages are provided and discussed in Section 5. Finally, a summary of results and conclusions are given in Section 6.
2. QUASI-ZENITH SATELLITE SYSTEM
QZSS is a Japanese Regional Satellite Navigation System (RNSS). When fully deployed in 2018, it will consist of three QZSS satellites placed in Highly Inclined Elliptical Orbits (HEO) and one Geostationary (GEO) satellite (Clark, Reference Clark2013). The HEO satellites have a similar orbital period to equatorial geostationary satellites, but have a large orbital inclination angle from the equatorial plane, so that the ground track moves with respect to the Earth's surface. The orbit configuration of these inclined QZSS satellites provides continuous coverage at a high elevation angle, thus improving the performance of satellite navigation in areas of Japan that challenge traditional satellite positioning capabilities, e.g., natural and urban canyons. While built primarily for users in Japan, the orbit design of QZSS offers significant advantages to neighbouring East Asian and Oceania countries centred along the 135° E meridian line. The first QZSS satellite, QZS-1 nicknamed ‘Michibiki’, was launched on 11 September 2010. Japan Aerospace Exploration Agency (JAXA) declared QZS-1 user-ready in June 2011 (JAXA, 2013).
QZSS is intended as a regional augmentation system for GNSS, aimed at enhancing the availability and the performance of GNSS-based Positioning Navigation and Timing (PNT). In addition to transmitting navigation signals similar in structure, frequency and spreading codes to GPS, i.e., L1C/A, L1C, L2C, L5, QZSS also transmits two augmentation signals, i.e., L1-SAIF (Sub-metre Augmentation with Integrity Function) and LEX. The L1-SAIF signal provides wide-area differential corrections, allowing sub-metre positioning accuracy, coupled with integrity data for safety-of-life services. This system is similar to the US Wide-Area Augmentation System (WAAS). The LEX signal, on the other hand, is unique to QZSS. It delivers correction messages, such as precise orbit and clock corrections, that will augment the current performance of single receiver point positioning.
In order to cover the East Asia and Oceania region, the QZSS will make use of at least three HEO and one GEO satellites. The first satellite, QZS-1, intended for system evaluation was launched into a HEO orbit. The orbit parameters and ground track of the QZS-1 satellite are presented in Table 1. The proposed two HEO satellites to be launched by 2018 are expected to have the same ground track with eight hours of offset, i.e. the same semi-major axis, eccentricity, inclination and perigee with ±120° offset in right ascension angle. All QZSS satellites have a mean anomaly of 135° E central longitude. This orbit has good coverage over the East Asia and Oceania region, with a high elevation at around 135° E meridian and between 40° N and 40° S latitude.
Table 1. QZS-1 HEO parameters.

3. THE L-BAND EXPERIMENTAL SIGNAL AND MESSAGES
The QZSS LEX signal is an experimental performance enhancement signal transmitted on 1278·5 MHz, which shares the same centre frequency as the Galileo E6 signal. The signal has a frequency bandwidth of 39·0 MHz (±19·5 MHz) and received minimum power level of −155·7 dBW. The LEX baseband signal is right-hand circularly polarised and is modulated by Bi-Phase Shift Key (BPSK) with a chipping rate of 5·115 Mcps. The signal has a dual-code structure with short and long Pseudo Random Numbers (PRN) code interleaved chip by chip, each having 2·5575 Mcps. The long code is dataless while the short code is modulated by Reed-Solomon encoded navigation messages with Code-Shift Keying (CSK) that realises a high data transmission rate of 2,000 bps (JAXA, 2013).
Figure 1 illustrates the navigation message modulation for the LEX signal. The LEX navigation message is grouped in frames of 250 symbols which are transmitted every second, eight bits indicating the satellite transmitting the message (PRN 193 for the QZS-1 and PRNs 194 to 196 for the next three QZSS satellites), eight bits indicating the type of message and an alert flag of one bit are added to 1695 bits of data to form 214 symbols of eight bits each. The 214 symbols are encoded into 246 symbols using a shortened Reed-Solomon code. Finally four preamble symbols i.e. “1A, CF, FC, 1D” are added.

Figure 1. LEX signal code modulation (JAXA, 2013).
Most of the factors governing the availability of the LEX receiver can be considered either independent of the receiver geographical location or to be highly correlated with the elevation of the satellite. The probability of successfully decoding the CSK modulated LEX message, as a function of the QZS-1 satellite elevation is shown in Figure 2. The results were obtained from three days of observations in Melbourne from 8–10 March 2013 (Choy et al., Reference Choy, Harima, Li, Wakabayashi, Tateshita, Kogure and Rizos2013). As shown in Figure 2, the LEX signal availability can be expected to be over 90% when the QZS-1 satellite is above 40° elevation. These results were obtained using a standard patch antenna and a LEX receiver that uses L1 C/A code as a reference to demodulate the CSK LEX messages. Receivers based on this technique are especially sensitive to frequency dependent interference such as multipath.

Figure 2. LEX message availability as a function of QZS-1 satellite elevation.
The left plot in Figure 3 shows contour lines representing the number of hours a day the QZS-1 satellite can be seen at more than 40° elevation over the East Asia and Oceania region. The right plot in Figure 3 shows the estimated number of hours a day at least one QZSS satellite will be over 40° elevation. The LEX signal is expected to be available 24-hours a day for most of the East Asia and Oceania region by 2018 when three active HEO satellites are declared fully operational.

Figure 3. Current LEX message availability with one QZSS satellite (left). Expected LEX message availability with three active HEO satellites in 2018 (right).
At present, the QZSS LEX signal does not only contain correction messages for PPP. It also carries correction messages for other PNT application demonstrations by several organisations in Japan including the JAXA, Satellite Positioning Research and Application Centre, National Institute of Information and Communications Technology, and Geospatial Information Authority of Japan. For PPP applications, LEX message types 10–12 can be used. LEX message types 10 and 11 are the ‘first generation’ of LEX-PPP corrections. The quality of those products was marginal due to the limited number of ground reference stations used in computing the orbits and clocks (Choy et al., Reference Choy, Harima, Li, Wakabayashi, Tateshita, Kogure and Rizos2013). In April 2013, JAXA began transmission on an experimental basis of MADOCA-LEX (Multi-GNSS Advanced Demonstration tool for Orbit and Clock Analysis) corrections (Kawate et al., Reference Kawate, Miyoshi, Nakamura, Kogure, Soga, Hirahara, Yasuda and Takasu2013) using message type 12 based on the RTCM-SSR (Radio Technical Commission for Maritime Services State Space Representation) message format. The corrections have wide-area validity and thus can be used over the QZSS coverage region. The MADOCA software was developed by NEC, Tokyo University of Marine Science and Technology, and JAXA for estimation of multi-GNSS satellite orbits and clocks. The quoted accuracy of the MADOCA GPS orbits and clocks is 4 cm and 0·1 ns, respectively (JAXA, 2014).
Table 2 shows the type of corrections included in the MADOCA-LEX messages and their corresponding broadcast and update rates in unit of second as of November 2013. Currently the MADOCA-LEX messages include orbit corrections, clock corrections, User Range Accuracy (URA) for both GPS and QZS-1 satellites, and code bias for GPS-only satellites. JAXA has plans in the near future to include the Russian's GLONASS correction messages to allow multi-GNSS PPP and phase bias messages for PPP ambiguity resolution.
Table 2. Broadcast rate and update interval of the MADOCA-LEX corrections.

The MADOCA-LEX messages are coded within the 1695 bits of data following a format derived from the RTCM 3·2 standard as illustrated in Figure 4. Of the 1695 bits allocated for data, 33 bits are used to transmit the time in which the LEX message is transmitted. The contents of the RTCM 3·2 frame, with the exception of the header and parity check bits, are allocated in the remaining 1662 bits.
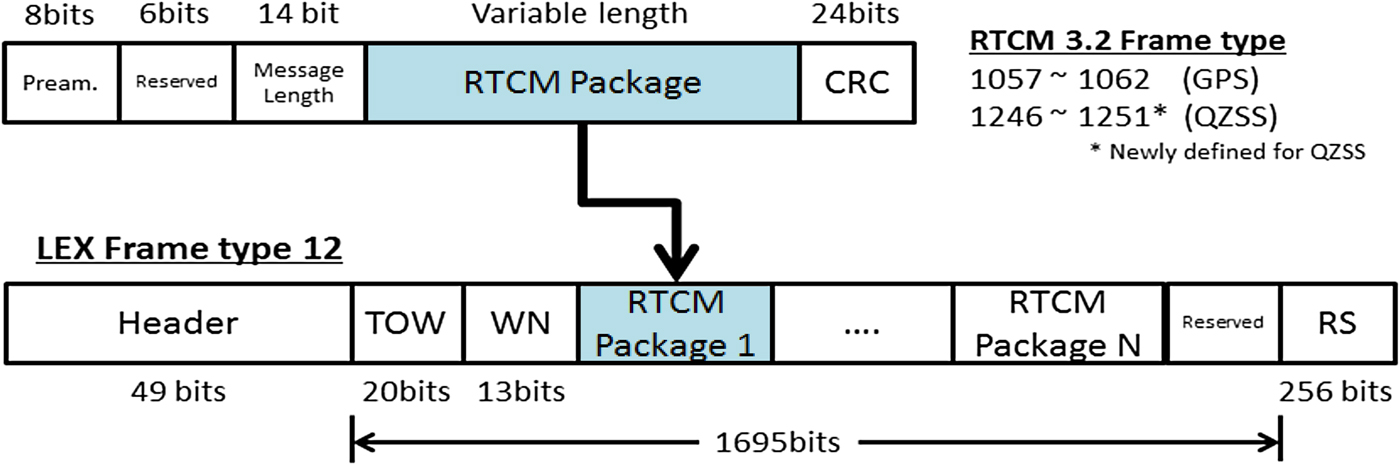
Figure 4. MADOCA-LEX message data format.
4. MADOCA-LEX ORBIT AND CLOCK CORRECTIONS
As PPP processing relies on precise information on the satellite orbits and clocks for high accuracy point positioning, the quality of these corrections will have direct impact on the achievable positioning accuracy as well as the solution convergence time. In this section we present an assessment of the quality of the MADOCA-LEX orbit and clock corrections for GPS-only satellites. The comparison was made using five days of MADOCA-LEX data, from 17 to 21 September 2013, collected from a monitoring station (station ID: RJAP) equipped with a LEX receiver in Melbourne, Australia. Note that RJAP is not an IGS station. The collected data was compared to the IGS Final products. The IGS Final GPS orbits have an accuracy of 2·5 cm and the clocks are accurate to 75 ps (RMS) with a standard deviation of 20 ps (IGS, 2014). The IGS-RTS products, in particular the mountpoint CLK 11 stream produced by BKG (Bundesamt für Kartographie und Geodäsie) were also assessed in this study and included herein for comparison purpose. The IGS-RTS CLK11 stream, hereafter called IGS-RT, was selected among the IGS real-time streams for its precedent of being successfully tested with the RTKLIB software (Takasu, Reference Takasu2011) used in this project.
Table 3 shows the mean, Standard Deviation (STD) and Root Mean Square (RMS) values of the differences between the MADOCA-LEX, IGS-RT corrections with the IGS Final products. The orbital errors are presented as radial, along and cross track components shown in metres (m) while the clock correction errors are in units of nanoseconds (ns). The common offset between the system clocks with the IGS timescale has been removed for all satellites. The clock STD and RMS are presented in the table. Figure 5 shows the time series for the differences between the MADOCA-LEX orbit and clock corrections with the IGS Final products. The period between 5:00 UTC and 12:00 UTC in which no results are presented corresponds to the period when the MADOCA-LEX messages could not be decoded reliably. This is due to the low elevation of the QZS-1 satellite seen from the Melbourne RJAP reference station.

Figure 5. Orbit and clock errors of the MADOCA-LEX corrections with respect to the IGS Final products.
Table 3. Orbit and clock errors of MADOCA-LEX and IGS-RT products.

The orbit errors of the MADOCA-LEX products are about as twice as large as those obtained from the IGS-RT stream for the measured timeframe. However, the contribution of the orbit errors in the Signal-in-Space Range Error (SISRE) was less than 0·050 m (0·037 m for MADOCA-LEX and 0·018 m for IGS-RT). This made the clock error, equivalent to 0·230 m for MADOCA-LEX and 0·210 m for IGS-RT, the dominant factor in determining the SISRE. As a consequence, the SISRE is expected to differ less by than 10%. For the case of the RJAP station, the measured SISRE was 0·227 m for MADOCA-LEX and 0·210 m for IGS-RT.
5. REAL-TIME PRECISE POINT POSITIONING
The MADOCA-LEX products were also evaluated in terms of real-time PPP solutions in static and kinematic processing modes. No phase ambiguities were resolved in this analysis and the solutions presented herein were based on ambiguity-float ionosphere-free PPP solutions. We present two tests, one at a fixed-point and a moving vehicle test. The fixed-point test consists of two modes of processing. A static PPP processing using MADOCA-LEX data collected on 1 August 2013 and a kinematic PPP processing using data collected from 17–22 September 2013. The moving vehicle test, on the other hand, was carried out on 23 October 2013. All processing was done in RTKLIB software version 2.4.2 (Takasu, Reference Takasu2011) and the results were GPS-only solutions. Dual frequency geodetic grade GNSS receivers were used and the MADOCA-LEX corrections were collected using an independent LEX receiver. The PPP solutions from the IGS-RT (CLK 11) products were also evaluated and the corrections were streamed through a mobile data router connected to a cellular network.
5.1. Fixed-Point Test
The fixed-point data were collected at RJAP station in Melbourne, Australia. The GNSS receiver installed at this station is a Javad DELTA-G3 T receiver and is connected to the Javad GrAnt-G3 T antenna shown in Figure 6. The LEX antenna, i.e. a G5Ant-2A4MNS1 from ANTCOM, is also mounted on a pillar, as depicted in Figure 6. The LEX messages were demodulated and decoded by a software receiver known as the LEX Message Streamer developed by Lighthouse Technology and Consulting Co. Ltd. The known coordinates of the RJAP reference station in ITRF08 with RMS errors of 2 cm were used as ‘ground-truth’ to evaluate the PPP estimates.

Figure 6. RJAP station at RMIT Bundoora campus in Melbourne, Australia.
The data used for static PPP processing was collected from 05:30 UTC to 23:30 UTC on 1 August 2013. The mean, STD and RMS error of static PPP using MADOCA-LEX corrections are presented in Table 4. Static PPP results using IGS-RT products are also presented. The results in Table 4 were calculated without taking into account the first two hours of solutions. This was to allow the PPP solutions to converge and stabilise. The three-dimensional RMS error for PPP using MADOCA-LEX corrections is 0·041 m, which is about 25% larger than the IGS-RT solutions. The time series for the first 12 hours of the static tests is shown in Figure 7. The MADOCA-LEX solutions are shown in blue, while the IGS-RT solutions are shown in green.

Figure 7. Real-time static PPP position errors from using the MADOCA-LEX (blue) and the IGS-RT corrections (green).
Table 4. Positioning errors for static PPP after two hours of convergence.

The real-time kinematic PPP test using MADOCA-LEX corrections presented in this section was performed from 17–21 September 2013 with a total of eight tests ranging from three to nine hours. The mean, STD and RMS errors of the kinematic PPP processing using these corrections are presented in Table 5. The statistics for the kinematic PPP solutions using IGS-RT products are also presented for comparison. A total of 11 tests ranging from three to nine hours were undertaken using the IGS-RT products between 17 and 22 September 2013. Again, the values presented in Table 5 were calculated after discarding the first two hours of data for each test to allow for the solutions to converge. The reason for the different number of datasets used is due to the availability of the MADOCA-LEX corrections, which cannot be successfully decoded when the satellite elevation is low. The three-dimensional RMS error for PPP using MADOCA-LEX solutions is 0·145 m, which is about 18% larger than the IGS-RT solutions. Figure 8 shows the time series of the real-time kinematic PPP position errors using the MADOCA-LEX corrections. As depicted in Figure 8, the convergence time of the PPP solutions using the real-time MADOCA-LEX corrections appears to be over two hours for some cases.

Figure 8. Position errors for kinematic PPP using the MADOCA-LEX corrections on a fixed point.
Table 5. Positioning errors for kinematic PPP after two hours of convergence on a fixed point.

Tables 6 and 7 present the RMS errors for the East, North and Up components of the kinematic PPP solutions at different convergence times in minutes using MADOCA-LEX and the IGS-RT corrections, respectively. The values in the tables were calculated using measurements corresponding to a 10 minute period just after the convergence time. For example, the RMS errors at 30 minutes time of convergence were computed based on the position estimates between 30–40 minutes. The three-dimensional RMS errors of the MADOCA-LEX solutions from 120 to 130 minutes after a Kalman filter re-initialization is 0·200 m, that is 38% higher than the RMS errors calculated from 120 minutes to the end of each test.
Table 6. RMS errors for kinematic PPP using MADOCA-LEX products on a fixed point.

Table 7. RMS errors for kinematic PPP using IGS-RT (CLK 11) products on a fixed point.

For comparison purposes, the RMS errors of the position estimates using the IGS-RT products at different convergence times are also shown in Table 7. Similar to the MADOCA-LEX solutions, the three-dimensional position RMS error derived from using the IGS-RT products is 26% higher than the final value, i.e., the RMS errors calculated from 120 minutes to the end of each test. Therefore 120 minutes may not be enough in some instances to allow for complete solution convergence. It is worth noting that the difference in three-dimensional position RMS errors between 90 and 120 minutes of convergence is less than 10% for both MADOCA-LEX and IGS-RT.
5.2. Moving Vehicle Test
The moving vehicle test presented here was carried out on 22 October 2013 from 21:15 UTC to 22:20 UTC in Centennial Park, Sydney, Australia (23 October 2013 from 8:15–9:20 am local time). The GNSS and LEX antennas were mounted on top of a car roof and were connected to receivers placed inside the car. As a reference for evaluating the real-time kinematic PPP solutions, network-RTK positions were obtained from a Leica GX1200 receiver connected to the CORSnet New South Wales (CORSnet-NSW) network-RTK service (NSW LPI, 2013). The network-RTK solutions are expected to be accurate to 2 cm horizontally and 5 cm vertically. The GNSS receiver used for PPP positioning was a Novatel OEM4 receiver connected through a splitter to the Leica receiver's antenna. Figure 9 shows the ground track of the moving vehicle and its surrounding environment (open sky condition). The car was left stationary for approximately 180 minutes to allow the PPP solutions to converge before moving up to a speed of 10 kmh−1. Two real-time kinematic PPP solutions were obtained, i.e., MADOCA-LEX (corrections transmitted on the QZS-1 LEX signal), and the IGS-RT CLK 11(corrections transmitted through a mobile phone network).

Figure 9. Ground track of the vehicle test performed at Sydney.
The mean, STD and RMS errors of the kinematic PPP solutions computed from using MADOCA-LEX, IGS-RT corrections are presented in Table 8. Post-processed solutions obtained from the online NRCan PPP service were provided for comparison (NRCan, 2013). The errors in the East, North and Up components were the differences between the PPP solutions and the network-RTK estimates. The three-dimensional position RMS errors of the real-time kinematic PPP using MADOCA-LEX solutions were 0·113 m, and 0·121 m using the IGS-RT products. The 3-dimentional RMS errors of the post-processed PPP solutions were 0·102 m. The errors for kinematic PPP using IGS-RT products were slightly higher than those obtained using MADOCA-LEX. Although the exact reason governing this performance difference needs to be further investigated, it is believed that a combination of factors such differences in starting time (a priori coordinates), quality of the corrections, and connectivity to the terrestrial mobile network affected the convergence of the PPP solutions using IGS-RT corrections. The RMS clock error of the IGS-RT corrections when compared to the final IGS clocks was 1·35 ns during the vehicle test, while the RMS clock error using MADOCA-LEX corrections was 0·78 ns. Also the solutions using IGS-RT products started 28 seconds later than those using MADOCA-LEX products due to delays in negotiating with the mobile network, potentially giving different starting conditions. Figure 10 shows the time series of the car's positioning errors based on the MADOCA-LEX in blue, IGS-RT corrections in green, and NRCan post-processed PPP solutions in black. The NRCan PPP solutions are based on backward-smoothed solutions, which do not depict convergence.

Figure 10. Real-time kinematic PPP position errors of the moving vehicle using MADOCA-LEX (blue) and IGS-RT (green) corrections. Post-processed NRCan PPP solutions (black) are shown for comparison.
Table 8. Position errors of the real-time PPP solutions in the moving vehicle test. Post-processed PPP solutions from the NRCan online processing service are included for comparison.

6. CONCLUSIONS
The Japanese QZSS system is an RNSS augmentation system that aims to improve GNSS satellites availability in the East Asia and Oceania region as well as to enhance performance of GNSS satellite-based PNT applications. One of the augmentation signals transmitted by the QZS-1 is the LEX signal. The LEX signal is designed to provide enhanced accuracy of GNSS-based PNT applications such as real-time PPP and timing. The services provided by the LEX signal are expected to cover most of the East Asia and Oceania region by 2018 when the system reaches full operational capability with three HEO and one GEO satellites.
One of the services provided by the LEX signal is the transmission of MADOCA-LEX messages that contain precise orbit and clock corrections that allow for real-time PPP. In the present paper the performance of real-time PPP using MADOCA-LEX messages was evaluated at a fixed-point and in a moving vehicle. The real-time PPP solutions derived from using the IGS-RT (CLK 11) corrections stream were also presented for comparison purpose. For the static PPP, a three-dimentional accuracy of 0·041 m can be expected after two hours of convergence. This accuracy is comparable with those obtained with the IGS-RT corrections, i.e., 0·033 m. For kinematic PPP, a three-dimentional accuracy of 0·200 m can be expected after 90 minutes of convergence and 0·145 m after two hours. These decimetre-level accuracies are obtained in both fixed-point and vehicle tests. These results are also similar to those obtained from using the IGS-RT products and from the post-processed NRCan PPP solutions. It is worth noting that both tests presented in this paper were carried out under open sky conditions. Therefore the performance of PPP under urban environment as well as the effects of the latency induced by the terrestrial or satellite communication links is expected to be less successful. JAXA is currently continuing its efforts to further improve and enhance the capabilities of the LEX signal to enhance high accuracy point positioning solutions.
ACKNOWLEDGEMENTS
This work is supported by the Australian Cooperative Research Centre for Spatial Information (CRC-SI). The project ‘High Accuracy Real-Time Positioning Utilising the Japanese Quasi Zenith Satellite System Augmentation System’ is a collaborative project between the CRC-SI and Japan Aerospace Exploration Agency (JAXA). The research consortium is made up by six Australian organisations, i.e., RMIT University, University of New South Wales, the Victorian State Government Department of Environment and Primary Industries, the New South Wales Government (NSW) Land and Property Information (LPI), Geoscience Australia, Spatial Information Systems Research Ltd, and JAXA. The authors would like to thank Mr. Thomas Grinter from NSW LPI for providing field assistance and support in moving vehicle test. The effort of the IGS to provide real-time precise satellite orbits and clocks is gratefully acknowledged. Lastly, the authors would also like to thank the anonymous reviewers for their helpful suggestions to improve the manuscript.




















