Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-05T11:20:52.726Z Has data issue: false hasContentIssue false
  • English
  • Français

The Exponential Integral Frequency Distribution

Published online by Cambridge University Press:  18 January 2010

J. B. Parker
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent note, D. A. Lloyd has obtained a formula for the frequency distribution of time dependent errors in terms of the exponential integral

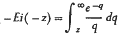
This note clarifies Lloyd's derivations by referring to a theoretically identical, though conceptually different, time-independent, physical model, relates this distribution to one described by Anderson and concludes with a short appreciation of the role of the negative exponential distribution in navigational studies.

Type
Forum
Information
The Journal of Navigation , Volume 19 , Issue 4 , October 1966 , pp. 526 - 529
Copyright
Copyright © The Royal Institute of Navigation 1966

References

REFERENCES

1Lloyd, D. A. (1966). A probability distribution for a time-varying quantity. This Journal, 19, 119.Google Scholar
2Anderson, E. W. (1965). Is the gaussian distribution normal? This Journal, 18, 65.Google Scholar
3 The accuracy of astronomical observations at sea (Working Party Report). This Journal, 10, 223.CrossRefGoogle Scholar
4Crossley, A. F. (1966). On the frequency distribution of large errors. This Journal, 19, 33.Google Scholar
5Parker, J. B. (1952). Simultaneous position data in the air. This Journal, 5, 235.Google Scholar