No CrossRef data available.
Published online by Cambridge University Press: 23 November 2009
In a notable series of articles, Hsu advances theoretical models which are used to graduate 7582 observations of aircraft lateral deviations. The goodness of fit of these models, as judged by the χ2 test, is satisfactory. Hsu's main theoretical model is the Double Double Exponential distribution (DDE), a three parameter model whose probability density function is given by
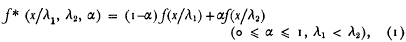
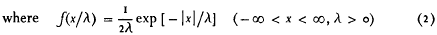
Other model types are also considered, such as the family of exponential power distributions whose probability density is cited by Hsu insection 9. This leads to a four-parameter model, and the fit is (not surprisingly) better even than that of the DDE.