1. INTRODUCTION
Multi-sensor data fusion has been widely used in modern civilian and military areas because sensor networks can provide more comprehensive information and more accurate state estimation of the target than a single sensor, such as Command, Control, Communications, Computers, Intelligence, Surveillance and Reconnaissance (C4ISR) and air-control systems (Progri, Reference Progri2011; Reference Progri2014). However, before the benefits of multi-sensor integration can be realized, the sensor registration problem (or alignment) must be addressed because of the existence of unavoidable systematic biases (SBs) which make the measurements deviate from the true target coordinates (TTCs). In this situation, when different sensors' measurements are transformed to a common reference frame, the estimation accuracy of the target location will be decreased, also, data disassociation and redundant tracks will occur, which can seriously harm the fusion. To overcome these adverse influences, several registration methods were developed (see Wang et al. (Reference Wang, Chen and Jia2012) for a brief introduction to these methods).
In contrast to stationary radar, mobile radar measurements contain simultaneous ABs of the platform including yaw, pitch and roll biases, which may occur due to accumulated biases in the gyros in the Inertial Measurement Units (IMU) of the Inertial Navigation System (INS) (Wang et al., Reference Wang, Chen and Jia2012; Carlson and Bott, Reference Carlson and Bott1973; King, Reference King1997). The most difficult thing for mobile radar registration is to estimate OBs and ABs simultaneously since their coupling is inevitable. According to different installation methods, mobile GSP or UGSP radar registration models should be considered because of different types of radar measurements (Wang et al., Reference Wang, Chen and Jia2012; Bhatti and Ochieng, Reference Bhatti and Ochieng2007). First, GSP radars are installed on a platform that can steadily follow a local ENU frame (Progri, Reference Progri2011; Reference Progri2014) by using real-time attitude information provided by the platform INS; i.e., the radar is insulated from the platform AAs. ABs in this situation assume a set of Euler angles between radar sensitive and ENU axes. Second, UGSP radar is: (1) installed directly on the platform with their sensitive axes coincident with the platform frame and (2) change simultaneously when the platform moves. Here, the true attitude angles (TAAs) of the platform are included in radar measurements. When these measurements are converted to a common reference frame, the real-time attitude angle information (containing ABs) provided by the INS is needed to rectify radar raw measurements; therefore, the common attribute for both kinds of mobile radar registration is to estimate OBs and ABs simultaneously.
For GSP mobile radar registration, previous works include: (1) Dela Cruz et al. (Reference Dela Cruz, Alouani, Rice and Blair1992) and Helmick and Rice (Reference Helmick and Rice1993) proposed a two-stepped method which estimates two types of biases separately by using KF twice, and this can only obtain relative bias estimations. (2) Bar-Shalom (Reference Bar-Shalom2001) introduced the observability analysis for the first time. (3) Wang et al. (Reference Wang, Chen and Jia2012) combined all OBs and ABs as a state vector to establish a registration model called AAM; however, AAM has poor estimation performance especially for the attitude and elevation biases because it does not consider the dependencies among biases. (4) We derived the equivalent radar measurement error expressions caused by ABs and proved that azimuth and yaw biases are dependent, and they should be united to form a new variable and then the system is observable (Chen et al., Reference Chen, Wang, Jia and Progri2012). We successively proposed an Optimized Bias Estimation Model (OBEM) (Wang et al., Reference Wang, Chen and Jia2012) and URM (Chen et al., Reference Chen, Wang, Jia and Progri2013) because in both models, the roll and pitch biases are omitted from the state vector; however, the estimation results of radar OBs contain the influences of ABs; therefore, both kinds of biases are unified to form new variables to make the new registration models observable. Since the magnitudes of the unified variables are not constants and change with different target coordinatesFootnote 2, the difference of OBEM and URM is that the latter divided the unified variables into two classes: (1) the first class that does not vary when the target moves represents the dependent component among different biases; and (2) the second class that changes with different target coordinates represents the independent component. For GSP mobile radars, since the GSP can track the ENU frame, variations of the target coordinates are small between two successive observation instances; the independent components are also small and are viewed as insignificant noises by URM when establishing the state equation. However, OBEM omits these insignificant variations. Since these variations are small, OBEM and URM have approximate performances. (5) For UGSP mobile radars, Herman and Poore (Reference Herman and Poore2006) and Kragel et al. (Reference Kragel, Danford, Herman and Poore2007) analysed the dependencies between different biases qualitatively by using Singular Value Decomposition (SVD), yielding similar possible dependencies among different biases as those of Chen et al. (Reference Chen, Wang, Jia and Progri2012).
The main purpose of this work is to establish the basic registration model for UGSP mobile radars and theoretically improve the understanding of mobile radar registration technology. For UGSP mobile radar, since radars simultaneously rotate with the platform, the target coordinates relative to radar measurement frame change rapidly, which weakens the dependencies among OBs and ABs and make the system observable, then both kinds of biases can be independently estimated and AAM may perform well although it cannot be used for GSP mobile radars because of dependencies and the un-observability of biases. On the contrary, URM may be inapplicable because the independent components viewed as noises increase rapidly in magnitude. In order to reconcile these results, AAM and URM are derived for UGSP mobile radar registration respectively. A simulated track is used to analyse both models, and the influences of the platform AAs on the observability of the system are shown. Radar OBs include slant, the gain of slant, azimuth, and elevation biases; radar measurements include the influences of the platform TAAs, TTCs, radar OBs and random measurement noises. The navigation information provided by an INS include the true yaw, pitch, roll angles of platform, and corresponding ABs. We assume: (1) all systematic biases are constants; (2) both radars have accurate geographical information of themselves; (3) radars are synchronized and have the same sampling intervals.
This paper is organized as follows. In Section 2, a basic description for biased mobile radar is given. The detailed derivation of AAM for UGSP mobile radar registration is given in Section 3 and the observability analysis for AAM is given in Section 4. In Section 5, the concise derivation of URM is given for comparison and simulated track data is used to test the performance of AAM. Finally, Section 6 summarizes the results. In Appendices A and B, the detailed derivations of AAM and URM applied to UGSP mobile radar registration are given, respectively.
2. PROBLEM DESCRIPTION
Consider an ith radar, where i={1, 2}, installed on an ith moving ship. The geographic coordinates of the ith ship are latitude Ls i, longitude Rs i, and altitude Hs i, which are known in real time. Four reference frames will be defined first for further discussions (Herman and Poore, Reference Herman and Poore2006).
(1) The body frame or platform frame is defined as a Cartesian rectangular coordinate system fixed relative to the ship. Its origin locates at the barycentre of the ship, its body axes are typically oriented relative to the ship such as x, y, and z axis denotes starboard, ahead, and dry (and right, nose, and top for an aircraft), respectively.
(2) The measurement frame or sensor frame, fixed relative to radar, with the centre of the sensor antenna taken as its origin. For UGSP mobile radar, the measurement frame is parallel to the body frame (see Figure 1(a)). Its y axis denotes zero-degree azimuth, and clock-wise direction denotes the increment of azimuth.
The subscript “p” (so-called “platform”) was used to identify body frame, and “s” denotes sensor frame.
(3) ENU frame has the same origin with the body frame; its x, y, and z axis denotes east, north, and up, respectively.
(4) Earth-centred Earth-fixed (ECEF) frame (Progri, Reference Progri2011; Reference Progri2014) has its origin located at the centre of the earth (Wang et al., Reference Wang, Chen, Jia and Progri2013): its x-axis passes through the Greenwich meridian, its z-axis coincides with the Earth's axis of rotation and its y-axis lies in the equatorial plane to form a right-handed coordinate system.

Figure 1. Illustration of UGSP mobile radar. (a) Illustration of body frame and sensor frame; (b) Conversion from body frame to ENU frame.
At each sampling instance, the rotation of the ship around its barycentre can pass on to the sensor frame which includes yaw (or course), pitch, and roll angles. Both frames have the same rotation angles because of the fixed joint between the sensor and the ship. These angles are defined in local ENU frame (“local” denotes that the origins of ENU and the body frames coincide) and denote the angles between the corresponding axes of both frames.
As shown in Figure 1(b), the transformation from the body frame to ENU is accomplished by first rotating about the y-axis of the platform frame by the roll angle ψ, then rotating about the intermediate x-axis by the pitch angle η, and rotating about the final z-axis by the yaw angle ϕ. The axes drawn in dashed lines in Figure 1(b) are intermediate axes. Customarily, the positive directions of ϕ and ψ abide by the left-hand rule about their corresponding rotation axes, and η abides by the right-hand rule (Figure 1(a)).
Measurements are generated in the sensor frame which include the TTCs relative to radar i such as true target range r it, azimuth θ it, and elevation ε it; OBs such as range bias Δr i, the gain of range k ri , azimuth bias Δθ i, and elevation bias Δε i; random measurement errors such as range noise δ ri, azimuth noise δ θi, and elevation noise δ si, these noises are additive Gaussian white noises. Most importantly, the true (not biased) AAs of the platform such as the true roll angle ψ it, pitch η it, and yaw ϕ it are included in the measurements, which are different from GSP mobile radar measurements.
The navigation information generated by the INS of the ith ship for rectifying radar raw measurements include the ship's roll angles, ψ i, pitch, η i, and yaw, ϕ i. Also, additive ABs are included in each output such as roll bias Δψ i, pitch bias Δη i, and yaw bias Δϕ i as shown in Figure 1(b). (Random noises of the INS are not considered for brevity. Positive directions of ABs are defined the same as their corresponding AAs.)
The main objective for mobile radar registration is to simultaneously: (1) estimate OBs and ABs using both radars' raw measurements; (2) use these estimations to rectify radar raw measurements. The registration model is discussed next in greater detail.
3. REGISTRATION MODEL
The main objective of the registration algorithm is to establish the equivalent measurement equation in a common reference frame: TTCs of the same target included in both radars' raw measurements are equal when they are converted to a common reference frame. Figure 2 illustrates the following adopted steps. First, radar OBs and random measurement errors included in the raw measurements are removed to obtain TTCs in the sensor frame. This is followed by a translation from the sensor frame to the platform frame because of the different locations of their origins. Then, the conversion to ENU frame is accomplished according to the navigation information provided by the INS that include ABs. Finally, the conversion from ENU to ECEF frame (Upadhyay et al., Reference Upadhyay, Progri, Lomas and Buckler1999) is used to obtain TTCs in the common reference frame.

Figure 2. Conversion of TTCs from radar raw measurements to ECEF frame for UGSP mobile radar.
3.1. The Equivalent Measurement equation
3.1.1. TTCs in the platform frame
Given the ith radar measurements [r i (k), θ i (k), ε i (k)], OBs [Δr ikri, Δθ i, Δε i], and random measurement errors [δ ri, (k), δ θ i (k), δ εi (k)], we can obtain TTCs in the sensor frame as follows
 $${\bf X}_{i\_s} (k) = \left[ {\matrix{ {x_{i\_s} (k)} \cr {y_{i\_s} (k)} \cr {z_{i\_s} (k)} \cr}} \right] = \left[ {\matrix{ {\Upsilon _i (k)s_{\vartheta _i (k)} c_{\epsilon _i (k)}} \cr {\Upsilon _i (k)c_{\vartheta _i (k)} c_{\epsilon _i (k)}} \cr {\Upsilon _i (k)s_{\epsilon _i (k)}} \cr}} \right]\left\{ {\matrix{ {\Upsilon _i (k) = r_i \left( k \right) - {\rm \Delta} r_i - k_{ri} r_{it} (k) - \delta _{ri} (k)} \cr {\vartheta _i (k) = \theta _i (k) - {\rm \Delta} \theta _i - \delta _{\theta i} (k)} \cr {\epsilon _i (k) = \varepsilon _i (k) - {\rm \Delta} \varepsilon _i - \delta _{\varepsilon i} (k)} \cr {c_a = {\rm cos(}a{\rm )},\; s_a = {\rm sin(}a{\rm )}} \cr}} \right.$$
$${\bf X}_{i\_s} (k) = \left[ {\matrix{ {x_{i\_s} (k)} \cr {y_{i\_s} (k)} \cr {z_{i\_s} (k)} \cr}} \right] = \left[ {\matrix{ {\Upsilon _i (k)s_{\vartheta _i (k)} c_{\epsilon _i (k)}} \cr {\Upsilon _i (k)c_{\vartheta _i (k)} c_{\epsilon _i (k)}} \cr {\Upsilon _i (k)s_{\epsilon _i (k)}} \cr}} \right]\left\{ {\matrix{ {\Upsilon _i (k) = r_i \left( k \right) - {\rm \Delta} r_i - k_{ri} r_{it} (k) - \delta _{ri} (k)} \cr {\vartheta _i (k) = \theta _i (k) - {\rm \Delta} \theta _i - \delta _{\theta i} (k)} \cr {\epsilon _i (k) = \varepsilon _i (k) - {\rm \Delta} \varepsilon _i - \delta _{\varepsilon i} (k)} \cr {c_a = {\rm cos(}a{\rm )},\; s_a = {\rm sin(}a{\rm )}} \cr}} \right.$$where Xi_s(k) denotes TTCs in the sensor frame at time instant k. Since the true range r it(k) is unknown, it can be approximated by the measurement r i (k).
Transition of TTCs from the sensor frame to the platform frame only contains a translation, which can be expressed as
where the superscript “T” denotes vector or matrix transposition, Xi_p(k) depicts TTCs in platform frame. ΔXi_s2p represents the position vector of the sensor frame origin o is in the platform frame, that is, the sensor installation position relative to the barycentre of the ship. ΔXi_s2p is a constant vector, it can be omitted in the paper for brevity because it is very small in magnitude compared with the target position vectors as shown in the right hand approximation of Equation (2).
Substituting Equation (1) into Equation (2), taking radar SBs and measurement errors as variables, using first-order Taylor series expansion about zero vectors (or Maclaurin Theorem expansion about the origin), Equation (2) can be approximated as
where
 $$\eqalign{ {\bf X}_i \, (k) = & \left[ {\matrix{ {\underbrace {r_i (k)s_{\theta _i (k)} c_{\varepsilon _i (k)}} _{x_i (k)}} \cr {\underbrace {r_i (k)c_{\theta _i (k)} c_{\varepsilon _i (k)}} _{y_i (k)}} \cr {\underbrace {r_i (k)s_{\varepsilon _i (k)}} _{z_i (k)}} \cr}} \right];{\bf A}_i (k) = \left. {\displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bf \beta} _i (k)}}} \right|_{\matrix{ {{\bf \beta} _i (k) = {\bf 0}} \cr {{\bf w}_i (k) = {\bf 0}} \cr}} ;\; \cr {\bf C}_i (k) = & \left. {\displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bf w}_i (k)}}} \right|_{\matrix{ {{\bf \beta} _i (k) = {\bf 0}} \cr {{\bf w}_i (k) = {\bf 0}} \cr}}} $$
$$\eqalign{ {\bf X}_i \, (k) = & \left[ {\matrix{ {\underbrace {r_i (k)s_{\theta _i (k)} c_{\varepsilon _i (k)}} _{x_i (k)}} \cr {\underbrace {r_i (k)c_{\theta _i (k)} c_{\varepsilon _i (k)}} _{y_i (k)}} \cr {\underbrace {r_i (k)s_{\varepsilon _i (k)}} _{z_i (k)}} \cr}} \right];{\bf A}_i (k) = \left. {\displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bf \beta} _i (k)}}} \right|_{\matrix{ {{\bf \beta} _i (k) = {\bf 0}} \cr {{\bf w}_i (k) = {\bf 0}} \cr}} ;\; \cr {\bf C}_i (k) = & \left. {\displaystyle{{\partial {\bf X}_{i\_p} (k)} \over {\partial {\bf w}_i (k)}}} \right|_{\matrix{ {{\bf \beta} _i (k) = {\bf 0}} \cr {{\bf w}_i (k) = {\bf 0}} \cr}}} $$3.1.2. Transition from platform frame to ENU frame
Transition from the platform frame to ENU can be described by three sequential rotation transformations. Each transformation can be described as one rotation matrix. According to the polarity definition of the AAs and the transition order, the true rotation matrix at observation time k can be written as true: (a) roll,
![]() ${\bf T}_{\psi _{it}} (k)$; (b) pitch,
${\bf T}_{\psi _{it}} (k)$; (b) pitch,
![]() ${\bf T}_{\eta _{it}} (k)$; and (c) yaw,
${\bf T}_{\eta _{it}} (k)$; and (c) yaw,
![]() ${\bf T}_{\phi _{it}} (k)$, rotation matrices
${\bf T}_{\phi _{it}} (k)$, rotation matrices
 $${\bf T}_{\psi _{it}} (k) = \left[ {\matrix{ {c_{\tilde \psi _i (k)}} & 0 & { - s_{\tilde \psi _i (k)}} \cr 0 & 1 & 0 \cr {s_{\tilde \psi _i (k)}} & 0 & {c_{\tilde \psi _i (k)}} \cr}} \right];\quad \tilde \psi _i (k) = \psi _i (k) - {\rm \Delta} \psi _i $$
$${\bf T}_{\psi _{it}} (k) = \left[ {\matrix{ {c_{\tilde \psi _i (k)}} & 0 & { - s_{\tilde \psi _i (k)}} \cr 0 & 1 & 0 \cr {s_{\tilde \psi _i (k)}} & 0 & {c_{\tilde \psi _i (k)}} \cr}} \right];\quad \tilde \psi _i (k) = \psi _i (k) - {\rm \Delta} \psi _i $$ $${\bf T}_{\eta _{it}} (k) = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {c_{\tilde \eta _i (k)}} & { - s_{\tilde \eta _i (k)}} \cr 0 & {s_{\tilde \eta _i (k)}} & {c_{\tilde \eta _i (k)}} \cr}} \right];\quad \tilde \eta _i (k) = \eta _i (k) - {\rm \Delta} \eta _i $$
$${\bf T}_{\eta _{it}} (k) = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {c_{\tilde \eta _i (k)}} & { - s_{\tilde \eta _i (k)}} \cr 0 & {s_{\tilde \eta _i (k)}} & {c_{\tilde \eta _i (k)}} \cr}} \right];\quad \tilde \eta _i (k) = \eta _i (k) - {\rm \Delta} \eta _i $$ $${\bf T}_{\phi _{it}} (k) = \left[ {\matrix{ {c_{\tilde \phi _i (k)}} & {s_{\tilde \phi _i (k)}} & 0 \cr { - s_{\tilde \phi _i (k)}} & {c_{\tilde \phi _i (k)}} & 0 \cr 0 & 0 & 1 \cr}} \right];\quad \tilde \phi _i (k) = \phi _i (k) - {\rm \Delta} \phi _i $$
$${\bf T}_{\phi _{it}} (k) = \left[ {\matrix{ {c_{\tilde \phi _i (k)}} & {s_{\tilde \phi _i (k)}} & 0 \cr { - s_{\tilde \phi _i (k)}} & {c_{\tilde \phi _i (k)}} & 0 \cr 0 & 0 & 1 \cr}} \right];\quad \tilde \phi _i (k) = \phi _i (k) - {\rm \Delta} \phi _i $$The above rotation matrices are orthogonal matrices which satisfy TT=T−1. Then, TTCs in ENU frame can be written as
 $${\bf X}_{i\_ENU} (k) = \left[ {x_{i\_ENU} (k),y_{i\_ENU} (k),z_{i\_ENU} (k)} \right]^T = \underbrace {{\bf T}_{\phi _{it}} (k){\bf T}_{\eta _{it}} (k){\bf T}_{\psi _{it}} (k)}_{{\bf T}_{it\_p2ENU} (k)}{\bf X}_{i\_p} (k)$$
$${\bf X}_{i\_ENU} (k) = \left[ {x_{i\_ENU} (k),y_{i\_ENU} (k),z_{i\_ENU} (k)} \right]^T = \underbrace {{\bf T}_{\phi _{it}} (k){\bf T}_{\eta _{it}} (k){\bf T}_{\psi _{it}} (k)}_{{\bf T}_{it\_p2ENU} (k)}{\bf X}_{i\_p} (k)$$Using first-order Taylor series expansion about attitude angle measurements, Tit_p2ENU(k) can be approximated as
where:
 $${\bf \Delta} _i (k) = \left[ {\matrix{ 0 & {{\rm \Delta} _{12}} & {{\rm \Delta} _{13}} \cr { - {\rm \Delta} _{12}} & 0 & {{\rm \Delta} _{23}} \cr { - {\rm \Delta} _{13}} & { - {\rm \Delta} _{23}} & 0 \cr}} \right]\left\{ {\matrix{ {{\rm \Delta} _{12} = - s_{\psi _i (k)} {\rm \Delta} \eta _i - c_{\eta _i (k)} c_{\psi _i (k)} {\rm \Delta} \phi _i} \cr {{\rm \Delta} _{13} = s_{\eta _i (k)} {\rm \Delta} \phi _i + {\rm \Delta} \psi _i} \cr {{\rm \Delta} _{23} = c_{\psi _i (k)} {\rm \Delta} \eta _i - c_{\eta _i (k)} s_{\psi _i (k)} {\rm \Delta} \phi _i} \cr}} \right.$$
$${\bf \Delta} _i (k) = \left[ {\matrix{ 0 & {{\rm \Delta} _{12}} & {{\rm \Delta} _{13}} \cr { - {\rm \Delta} _{12}} & 0 & {{\rm \Delta} _{23}} \cr { - {\rm \Delta} _{13}} & { - {\rm \Delta} _{23}} & 0 \cr}} \right]\left\{ {\matrix{ {{\rm \Delta} _{12} = - s_{\psi _i (k)} {\rm \Delta} \eta _i - c_{\eta _i (k)} c_{\psi _i (k)} {\rm \Delta} \phi _i} \cr {{\rm \Delta} _{13} = s_{\eta _i (k)} {\rm \Delta} \phi _i + {\rm \Delta} \psi _i} \cr {{\rm \Delta} _{23} = c_{\psi _i (k)} {\rm \Delta} \eta _i - c_{\eta _i (k)} s_{\psi _i (k)} {\rm \Delta} \phi _i} \cr}} \right.$$Detailed analytical derivations for Equation (8) are provided in Appendix A. Substituting Equation (8) into Equation (7), omitting higher order terms, yields the conversion of TTCs in the ENU frame
The last term of the right hand side of Equation (9) is
where:
 $${\bf D}_i (k) = \left[ {\matrix{ {\underbrace {d_{11} (k)}_{ - c_{\psi _i (k)} c_{\eta _i (k)} y_i (k) + s_{\eta _i (k)} z_i (k)}} & {\underbrace {d_{12} (k)}_{ - s_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{13} (k)}_{z_i (k)}} \cr {\underbrace {d_{21} \left( k \right)}_{c_{\eta _i (k)} c_{\psi _i (k)} x_i (k) - c_{\eta _i (k)} s_{\psi _i (k)} z_i (k)}} & {\underbrace {d_{22} (k)}_{s_{\psi _i (k)} x_i (k) + c_{\psi _i (k)} z_i (k)}} & {\underbrace {d_{23} (k)}_0} \cr {\underbrace {d_{31} (k)}_{ - s_{\eta _i (k)} x_i (k) + c_{\eta _i (k)} s_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{32} (k)}_{ - c_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{33} (k)}_{ - x_i (k)}} \cr}} \right]$$
$${\bf D}_i (k) = \left[ {\matrix{ {\underbrace {d_{11} (k)}_{ - c_{\psi _i (k)} c_{\eta _i (k)} y_i (k) + s_{\eta _i (k)} z_i (k)}} & {\underbrace {d_{12} (k)}_{ - s_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{13} (k)}_{z_i (k)}} \cr {\underbrace {d_{21} \left( k \right)}_{c_{\eta _i (k)} c_{\psi _i (k)} x_i (k) - c_{\eta _i (k)} s_{\psi _i (k)} z_i (k)}} & {\underbrace {d_{22} (k)}_{s_{\psi _i (k)} x_i (k) + c_{\psi _i (k)} z_i (k)}} & {\underbrace {d_{23} (k)}_0} \cr {\underbrace {d_{31} (k)}_{ - s_{\eta _i (k)} x_i (k) + c_{\eta _i (k)} s_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{32} (k)}_{ - c_{\psi _i (k)} y_i (k)}} & {\underbrace {d_{33} (k)}_{ - x_i (k)}} \cr}} \right]$$Substituting Equation (10) into Equation (9), we can obtain
3.1.3. Transition from ENU to ECEF frame
Assuming that the geographic coordinates of the ith ship can be obtained from Global Positioning System (GPS) in real-time (Progri, Reference Progri2011; Reference Progri2014), omitting constant position errors between the GPS antenna and the barycentre of the ship, the transition of TTCs from ENU to ECEF frame can be written as (Zhou et al., Reference Zhou, Henry and Martin1999):
 $${\bf X}_{i\_ \hskip .5pt ECEF} (k) = {\bf X}_{is} (k) + {\bf T}_i (k) \cdot \left\{ {\matrix{ {{\bf X}_{i\_ \hskip .5pt ENU} (k) \approx} \cr {{\bf T}_{i\_ \hskip .5pt p2ENU} \left( k \right)\left[ {\matrix{ {{\bf X}_i (k) + {\bf A}_i (k){\bf \beta} _i (k) +} \cr {{\bf C}_{ i} (k){\bf w}_i (k) + {\bf D}_i (k){\bf a}_i (k)} \cr}} \right]} \cr}} \right.$$
$${\bf X}_{i\_ \hskip .5pt ECEF} (k) = {\bf X}_{is} (k) + {\bf T}_i (k) \cdot \left\{ {\matrix{ {{\bf X}_{i\_ \hskip .5pt ENU} (k) \approx} \cr {{\bf T}_{i\_ \hskip .5pt p2ENU} \left( k \right)\left[ {\matrix{ {{\bf X}_i (k) + {\bf A}_i (k){\bf \beta} _i (k) +} \cr {{\bf C}_{ i} (k){\bf w}_i (k) + {\bf D}_i (k){\bf a}_i (k)} \cr}} \right]} \cr}} \right.$$where Xi_ECEF (k) denotes TTCs in ECEF obtained from the measurements of the ith radar. Xis denotes the ith radar ECEF coordinates converted from its geographic coordinates. Ti is the rotation matrix. Xis(k) and Ti(k) are only correlated with the geographic coordinates of the ith radar at time k, and,
 $${\bf T}_i (k) = \left[ {\matrix{ { - s_{Rs_i (k)}} & { - s_{Ls_i (k)} c_{Rs_i (k)}} & {c_{Ls_i (k)} c_{Rs_i (k)}} \cr {c_{Rs_i (k)}} & { - s_{Ls_i (k)} s_{Rs_i (k)}} & {c_{Ls_i (k)} s_{Rs_i (k)}} \cr 0 & {c_{Ls_i (k)}} & {s_{Ls_i (k)}} \cr}} \right]$$
$${\bf T}_i (k) = \left[ {\matrix{ { - s_{Rs_i (k)}} & { - s_{Ls_i (k)} c_{Rs_i (k)}} & {c_{Ls_i (k)} c_{Rs_i (k)}} \cr {c_{Rs_i (k)}} & { - s_{Ls_i (k)} s_{Rs_i (k)}} & {c_{Ls_i (k)} s_{Rs_i (k)}} \cr 0 & {c_{Ls_i (k)}} & {s_{Ls_i (k)}} \cr}} \right]$$3.1.4. The equivalent measurement equation
For registration equations, the selection of the state variables is critical. Usually all the biases are selected as state variables, however for the GSP mobile radar, since ABs are dependent with radar OBs, the dependent parts should be combined to form new state variables, or the system is unobservable. URM (Chen et al., Reference Chen, Wang, Jia and Progri2012) was proposed for just this reason. For UGSP mobile radar, AAs of the platform are included in the registration equations, which make the system observable (See Observability Analysis in Section 4). Thus, it is practical to select both OBs and ABs as variables and the algorithm yields the absolute attitude bias estimations as well as absolute OB estimations. The following is the establishment process of the equivalent measurement equation for registration.
Since both radars have the same initial condition (or starting ECEF vector)
Substituting Equation (12) into Equation (13), the equivalent measurement equations can be written as
All OBs and ABs of both radars are selected in the state vector as (the order of the variables can be changed)
 $${\bf \beta} = \left[ {\underbrace {{\rm \Delta} r_1, k_{r1}, {\rm \Delta} \theta _1, {\rm \Delta} \varepsilon _1} _{{\bf \beta} _1^T (k)},\underbrace {{\rm \Delta} r_2, k_{r2}, {\rm \Delta} \theta _2, {\rm \Delta} \varepsilon _2} _{{\bf \beta} _2^T (k)},\underbrace {{\rm \Delta} \phi _1, {\rm \Delta} \eta _1, {\rm \Delta} \psi _1} _{{\bf a}_1^T (k)},\underbrace {{\rm \Delta} \phi _2, {\rm \Delta} \eta _2, {\rm \Delta} \psi _2} _{{\bf a}_2^T (k)}} \right] ^T$$
$${\bf \beta} = \left[ {\underbrace {{\rm \Delta} r_1, k_{r1}, {\rm \Delta} \theta _1, {\rm \Delta} \varepsilon _1} _{{\bf \beta} _1^T (k)},\underbrace {{\rm \Delta} r_2, k_{r2}, {\rm \Delta} \theta _2, {\rm \Delta} \varepsilon _2} _{{\bf \beta} _2^T (k)},\underbrace {{\rm \Delta} \phi _1, {\rm \Delta} \eta _1, {\rm \Delta} \psi _1} _{{\bf a}_1^T (k)},\underbrace {{\rm \Delta} \phi _2, {\rm \Delta} \eta _2, {\rm \Delta} \psi _2} _{{\bf a}_2^T (k)}} \right] ^T$$Since all OBs and ABs are selected as state variables, we call this model as AAM. According to Equation (15), Equation (14) can be rewritten as:
where:
3.2. The state equation
SBs are usually time-invariant or slowly varying variables. They can be modelled as constants or constants plus small random zero-mean Gaussian white noises or first-order Gauss-Markov process with a slow time constant (Bar-Shalom, Reference Bar-Shalom2001). To reduce the estimate errors caused by the wrong state equation model and omitting the small noises of biases for brevity (Chen et al., Reference Chen, Wang, Jia and Progri2013), we assume that all SBs are time-invariant variables and the state equations can be written as:
KF can be used to estimate SBs via the dynamic Equations (16) and (17) for registration.
4. OBSERVABILITY ANALYSIS
It is proposed that the system composed of Equations (16) and (17) is observable when the AAs are time-varying. This is proved as follows: According to Equations (16) and (17), the N-step random observable matrix can be written as (Qin et al., Reference Qin, Zhang and Wang1998; Andrade-Cetto and Sanfeliu, Reference Andrade-Cetto and Sanfeliu2004; Hermann and Krener, Reference Hermann and Krener1977; Lee et al., Reference Lee, Wijesoma and Guzman2006; Tseng and Lee, Reference Tseng and Lee2007)
 $${\bf M}(k,k - N + 1) = \mathop \sum \limits_{i = k - N + 1}^k {\bf I} \times {\bf m}(i) \times {\bf I} = \mathop \sum \limits_{i = k - N + 1}^k {\bf m}(i)$$
$${\bf M}(k,k - N + 1) = \mathop \sum \limits_{i = k - N + 1}^k {\bf I} \times {\bf m}(i) \times {\bf I} = \mathop \sum \limits_{i = k - N + 1}^k {\bf m}(i)$$where:
m(i) is an n×n matrix (n is the dimension of β) and its rank is 3 because the rank of H(i) is 3; E{w(k)wT(k)}=R(k), E{x} denotes the expectation of random variable x. N is a positive integer which is unrelated to k. R(i) in Equation (18) is a constant matrix because random noises have the same variances at different time. The system is said to be observable when M is positive definite.
Comparing Di in Equation (10) and Ai in Equation (3), we know that in the coefficient matrix H, the coefficient column vectors corresponding to OBs are not proportional to those of ABs. Since AAs are time-varying, according to Equation (16), H(i) and Γ (i) are different at each time. if
where the symbol [x] denotes the nearest integer greater than or equal to x, then the rank of
![]() $\sum _{i = k - N + 1}^k {\bf m}(i)$ s equal to N, and M is positive definite, and the system is observable.
$\sum _{i = k - N + 1}^k {\bf m}(i)$ s equal to N, and M is positive definite, and the system is observable.
However, for GSP mobile radar, the GSP can make the radar insulated from the carrier's AAs, the coefficient column vectors of ABs do not contain the AAs of the carrier, then the column vectors corresponding to the azimuth bias and yaw bias are equal, and the proportion factors of the column vectors corresponding to pitch and roll biases to those of azimuth and elevation biases change in small quantities and can be viewed as constants. The same results are applied to the coefficient matrix, Γ (i). In this situation, M is not definite, and the system is unobservable; hence, URM was proposed which unites the azimuth bias and yaw bias as one variable and omits roll and pitch biases to form the state vector. Though the roll and pitch biases do not appear in the URM state vector, the estimations of azimuth and elevation biases contain their influences.
The observability of Equation (16) and (17) can also be proven by the equivalent radar measurement error expressions caused by the AAs.
According to Δi in Equation (8) and equivalent measurement error expressions derived for the first kind of mobile radars (see Wang et al., Reference Wang, Chen and Jia2012), the equivalent measurement error expressions caused by ABs for the UGSP mobile radars can be written as the equivalent: (1) range, Δr ci(Δϕ i, Δη i, Δψ i), (2) azimuth, Δθ ci(Δϕ i, Δη i, Δψ i), and (3) elevation, Δε ci(Δϕ i, Δη i, Δψ i), error:
 $${\rm \Delta} \varepsilon _{ci} ({\rm \Delta} \phi _i, {\rm \Delta} \eta _i, {\rm \Delta} \psi _i ) = \displaystyle{{ - x_{i\_ \hskip .5pt s} {\rm \Delta \Psi} - y_{i\_ \hskip .5pt s} {\rm \Delta \Pi}} \over {\sqrt {x_{i\_ \hskip .5pt s}^2 + y_{i\_ \hskip .5pt s}^2}}} + o({\rm \Delta} \phi _i, {\rm \Delta} \eta _i, {\rm \Delta} \psi _i )$$
$${\rm \Delta} \varepsilon _{ci} ({\rm \Delta} \phi _i, {\rm \Delta} \eta _i, {\rm \Delta} \psi _i ) = \displaystyle{{ - x_{i\_ \hskip .5pt s} {\rm \Delta \Psi} - y_{i\_ \hskip .5pt s} {\rm \Delta \Pi}} \over {\sqrt {x_{i\_ \hskip .5pt s}^2 + y_{i\_ \hskip .5pt s}^2}}} + o({\rm \Delta} \phi _i, {\rm \Delta} \eta _i, {\rm \Delta} \psi _i )$$where the time stamp “k” is omitted for brevity. [x i_s, yi_s, zi_s]T denotes TTCs in sensor frame. Since it cannot be obtained in practice, it is usually approximated by Xi in Equation (4).
Then the gross equivalent azimuth and elevation biases can be written respectively as
Since AAs are time-varying, gross equivalent biases vary quickly and cannot be used as constant variables. On the contrary, if AAs are zeros, which correspond to GSP mobile radar, Equations (23) and (24) vary slowly and can be viewed as one variable. This is the theoretical basis for URM.
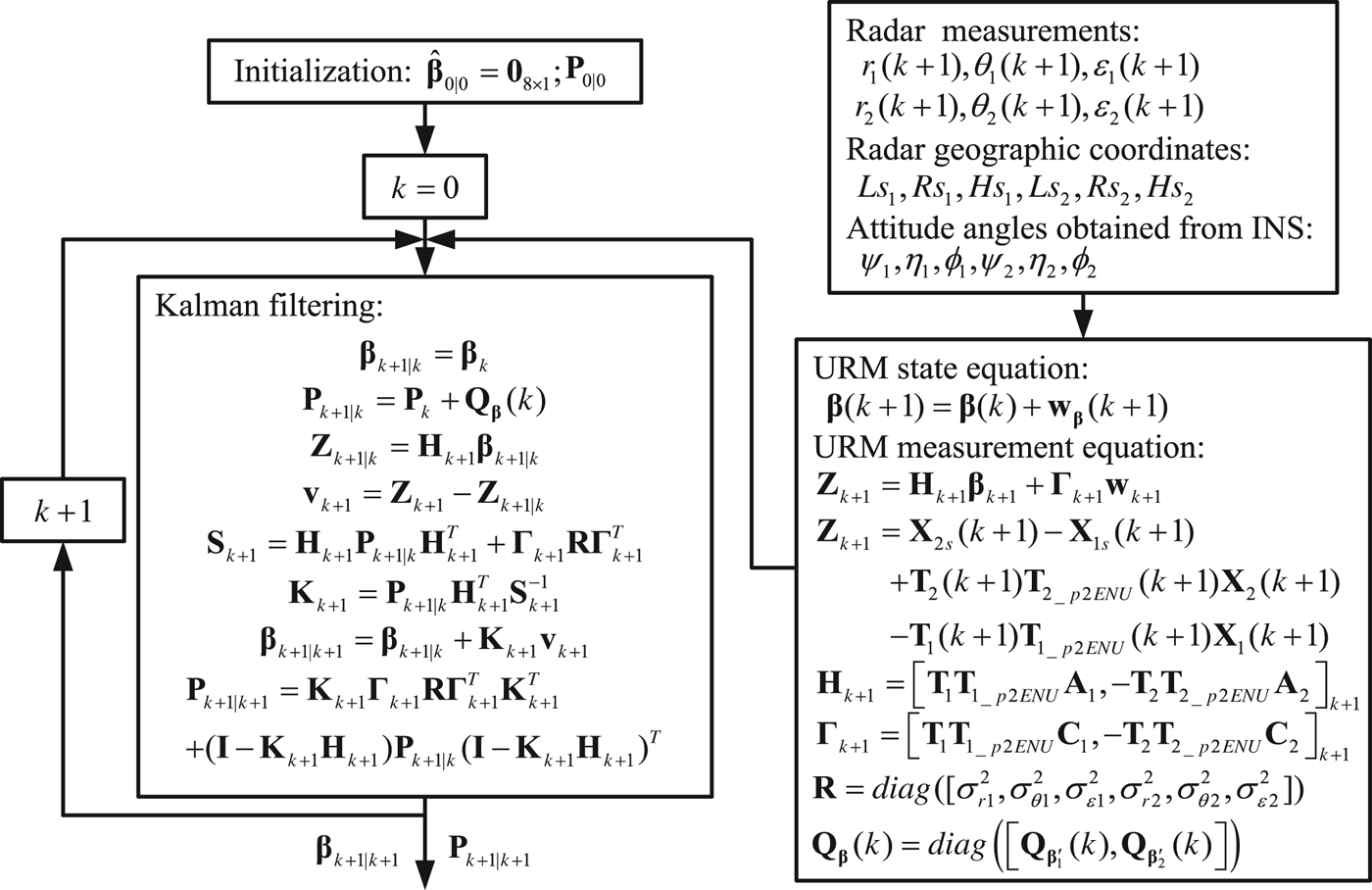
5. ALGORITHM ANALYSIS AND SIMULATION RESULTS
To assess (or compare and contrast) the performance of AAM used for UGSP mobile radar registration, URM is derived in this situation (see Figure 3). Because the main attribute of URM is that it only uses radar OBs as state variables, however, each OB variable contains the influences of all ABs (Chen et al., Reference Chen, Wang, Jia and Progri2013). Since the equivalent radar measurement errors caused by ABs vary with different target locations that can be seen in Equations (20)–(22), the variation parts are viewed as random noises.

Figure 3. Diagram of URM for the UGSP mobile radar.
The concise descriptions of URM are as follows:
5.1. URM for UGSP Mobile Radar Registration
The state vector of URM can be written as:
According to Equation (25), omitting the time argument “k”, Equation (14) can be revised to URM registration equation form as:
 $${\bf Z}_{URM} = \left[ {{\bf T}_1 {\bf T}_{1\_p2ENU} {\bf A}_1, - {\bf T}_2 {\bf T}_{2\_p2ENU} {\bf A}_2} \right]{\bf \beta} _{URM} + \left[ {{\bf T}_1 {\bf T}_{1\_p2ENU} {\bf C}_1, - {\bf T}_2 {\bf T}_{2\_p2ENU} {\bf C}_2} \right]{\bf w}$$
$${\bf Z}_{URM} = \left[ {{\bf T}_1 {\bf T}_{1\_p2ENU} {\bf A}_1, - {\bf T}_2 {\bf T}_{2\_p2ENU} {\bf A}_2} \right]{\bf \beta} _{URM} + \left[ {{\bf T}_1 {\bf T}_{1\_p2ENU} {\bf C}_1, - {\bf T}_2 {\bf T}_{2\_p2ENU} {\bf C}_2} \right]{\bf w}$$where
According to Equations (20)–(22), the state equation can be written as:
where:
 $${\bf w}_{{\bf \beta} _{URM}} (k) = \left[ {\underbrace {0,0,w_{d({\rm \Delta} \theta _1^')} (k),w_{d({\rm \Delta} \varepsilon _1 \hskip -2.8pt ' )} \left( k \right)}_{{\bf w}_{{\bf \beta} _1 \hskip -3pt '} (k)},\underbrace {0,0,w_{d({\rm \Delta} \theta _2 ^' )} \left( k \right),w_{d({\rm \Delta} \varepsilon _2 \hskip -3pt ' )} (k)}_{{\bf w}_{{\bf \beta} _2 \hskip -2.8pt '} (k)}} \right]^T $$
$${\bf w}_{{\bf \beta} _{URM}} (k) = \left[ {\underbrace {0,0,w_{d({\rm \Delta} \theta _1^')} (k),w_{d({\rm \Delta} \varepsilon _1 \hskip -2.8pt ' )} \left( k \right)}_{{\bf w}_{{\bf \beta} _1 \hskip -3pt '} (k)},\underbrace {0,0,w_{d({\rm \Delta} \theta _2 ^' )} \left( k \right),w_{d({\rm \Delta} \varepsilon _2 \hskip -3pt ' )} (k)}_{{\bf w}_{{\bf \beta} _2 \hskip -2.8pt '} (k)}} \right]^T $$![]() ${\bf w}_{{\bf \beta} _{URM}} $ can be viewed as zero-mean Gaussian white noises with the covariance matrix denoted as:
${\bf w}_{{\bf \beta} _{URM}} $ can be viewed as zero-mean Gaussian white noises with the covariance matrix denoted as:
 $${\bf Q}_{{\bf \beta} _{URM}} (k) = \left[ {\matrix{ {{\bf Q}_{{\bf \beta} _1^'} (k)} & 0 \cr 0 & {{\bf Q}_{{\bf \beta} _2^'} (k)} \cr}} \right] = \left[ {\matrix{ {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_1} & {c_1} \cr {c_1} & {b_1} \cr}} \cr}} _{{\bf Q}_{{\bf \beta} _1^'} (k)}} & {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr}} _{\bf 0}} \cr {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr}} _{\bf 0}} & {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_2} & {c_2} \cr {c_2} & {b_2} \cr}} \cr}} _{{\bf Q}_{{\bf \beta} _1^'} (k)}} \cr}} \right]$$
$${\bf Q}_{{\bf \beta} _{URM}} (k) = \left[ {\matrix{ {{\bf Q}_{{\bf \beta} _1^'} (k)} & 0 \cr 0 & {{\bf Q}_{{\bf \beta} _2^'} (k)} \cr}} \right] = \left[ {\matrix{ {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_1} & {c_1} \cr {c_1} & {b_1} \cr}} \cr}} _{{\bf Q}_{{\bf \beta} _1^'} (k)}} & {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr}} _{\bf 0}} \cr {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr}} _{\bf 0}} & {\underbrace {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_2} & {c_2} \cr {c_2} & {b_2} \cr}} \cr}} _{{\bf Q}_{{\bf \beta} _1^'} (k)}} \cr}} \right]$$where:
 $${\bf Q}_{{\bf \beta} _{\bf i}^'} (k) = E\left[ {{\bf w}_{{\bf \beta} _i^'} (k) \cdot {\bf w}_{{\bf \beta} _i^'} ^{\rm H} (k)} \right] = \left[ {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_i} & {c_i} \cr {c_i} & {b_i} \cr}} \cr}} \right];i = \left\{ {1,2} \right\}$$
$${\bf Q}_{{\bf \beta} _{\bf i}^'} (k) = E\left[ {{\bf w}_{{\bf \beta} _i^'} (k) \cdot {\bf w}_{{\bf \beta} _i^'} ^{\rm H} (k)} \right] = \left[ {\matrix{ {{\bf 0}_{2 \times 2}} & {{\bf 0}_{2 \times 2}} \cr {{\bf 0}_{2 \times 2}} & {\matrix{ {a_i} & {c_i} \cr {c_i} & {b_i} \cr}} \cr}} \right];i = \left\{ {1,2} \right\}$$Derivations of Equations (27)–(31) are given in Appendix B.
It should be noted that since the effects of the TAAs and ABs of the platform are only to make the measurements rotate, but the range between radar and the target will not be affected, the range and gain of the range biases remain constants, so zero entries appear in Equation (28).
The dynamic equations for URM are Equations (26) and (27); hence, KF can be used to estimate the gross equivalent biases to rectify raw radar measurements employing the diagram of URM shown in Figure 3.
5.2. Simulation Results
The proposed AAM and URM algorithms are compared by generating a common track for two radars installed directly on different ships. We assume that Ship 1 and Ship 2 are moving with a constant velocity model, and the initial geographical coordinates are [40°, 116°, 10 m], [40·75°, 115·34°,10 m], respectively. The initial states of both ships in their native ENU frame are [0 m, 10 m/s, 0 m, 10 m/s, 0 m,0 m/s]. In the state vector, the variables denote x-coordinate (east), x-velocity, y-coordinate (north), y-velocity, z-coordinate (up), and z-velocity, respectively.
The standard deviations of both ships' process noise are equal which are given in x, y, and z coordinates by [0·1, 0·1, 0] m/s2, respectively. All the TAAs of both ships make simple harmonic motions with 9 s motion periods.
To compare the influences of the AAs on the bias estimations, two scenarios are simulated. (1) The true amplitudes of yaw, pitch, and roll of both ships are set to 20°; (2) Changing the amplitudes to 5°. The initial phases of the AAs are random values.
The fusion centre locates at the initial position of Ship 1. A constant velocity model is also used for the target. The initial state of the target in the fusion centre is [60 km, 170 m/s, 30 km, 30 m/s, 5 km, 1 m/s].
The standard deviations of the process noise in x, y, and z coordinates are set to 1 m/s2,1 m/s2, and 0·1 m/s2, respectively. The geometry of radars and target is shown in Figure 4. The true systematic OBs of both radars are assumed to be constant and equal as Δr i=300 m, k ri=0·01, Δθ i=2°, and Δε i=2° respectively.

Figure 4. The geometry of target and radar.
The standard deviations of random measurement noises for both radars are σ ri=50 m, σ θ i=0·5°, and σ εi=0·5° respectively, and ABs of both platforms are also assumed to be constant and equal as Δϕ i=1°, Δη i=1°, and ψ i=1° respectively. It is assumed that both radars are synchronized with the same sampling intervals T=5 s. 200 scans of the target are simulated and the number of Monte Carlo runs is set to 100. Figures 5 and 6 contain all RMSEs of the bias estimations and the rectified target coordinates estimations.

Figure 5. RMSEs of bias estimations using the proposed algorithm (AAM). (a) gross range bias; (b) azimuth bias; (c) elevation bias; (d) yaw bias; (e) pitch bias; (f) roll bias.

Figure 6. RMSEs of TTCs in xyz-coordinates after rectifying radar 1 measurements by using bias estimations. (a), (b), (c) denote x-, y-, and z-coordinates, respectively where the attitude amplitudes equal to 20°; (d), (e), (f) denote x-, y-, and z-coordinates, respectively where the attitude amplitudes equal to 5°.
Figure 5 depicts RMSEs of AAM for OBs and ABs of both radars. In Figure 5(a), the gross range bias denotes the gross range bias containing the sum of range bias and the range errors caused by the gain of the range bias. (a)–(c) are the RMSEs of OBs and (d)–(f) are the RMSEs of ABs. The red lines denote the amplitudes of AAs of 20°; and the blue lines of 5°, the thin and thick lines represent the results of Radar 1 and Radar 2 respectively. The dotted lines represent the corresponding CRLBs (Detailed derivations of CRLB can be obtained in Chen et al., Reference Chen, Wang, Jia and Progri2013; Kay, Reference Kay1993; Progri, Reference Progri2011).
ABs can be well estimated for UGSP mobile radar, which demonstrates further that the observability is the main reason for the attitude bias estimation performances because the swaying of the radar antenna is equivalent to the scatter of the target coordinates, which can reduce the dependencies among OBs and ABs in the registration equations. The periodicity of the attitude bias CRLBs (Chen et al., Reference Chen, Wang, Jia and Progri2013) come from the periodicity of the AAs in Δi, see Equations (9) and (16).
Figure 6 depicts RMSEs of the rectified raw measurements in each axis of ENU frame, where the raw measurements are rectified by the estimated biases. (a)–(c) represent the case when the attitude amplitudes are 20°, and (d)–(f) are 5°. The red lines in Figure 6 denote the rectified measurements by using AAM estimations, and the blue lines denote the rectified measurements by using URM estimations. The asterisks represent RMSEs of the raw measurements rectified by the raw output of the INS. RMSEs of the rectified measurements by using AAM are more than 500 m smaller than by URM in all directions, which proves that AAM is better than URM for the mobile UGSP radars.
The CRLB of the equivalent bias estimation results obtained from URM are not given in the work for brevity. However, the performance of URM can be seen in Figure 6 which manifests that URM is inferior to AAM especially when the platform has bigger swaying amplitudes. Comparing the estimation results when the attitude amplitudes are 20° with those at 5°, we infer that the larger the amplitudes the better the estimation results because the larger amplitudes are equivalent to more scattering of the target coordinates in space, which can improve the observability of the system and the estimation accuracies. It should be noted that radar-scanning period and fluctuating periods of the ships' AAs should be not exactly integral multiples to ensure the ship's AAs are different at different observation instances.
6. SUMMARY AND CONCLUSIONS
Since the dependencies between ABs and OBs are related to the spatial distribution of targets, the more scattered the targets are, the weaker the dependencies become; hence, the better the observability of the system is. For mobile UGSP radar which is installed directly on and sways with the platform, the time-varying AAs of the platform are included in radar measurements, which makes the distribution of the same target in the radar measurement frame more scattered than for mobile GSP radars; i.e., for mobile UGSP radar, the observability of both kinds of biases is better than for GSP ones; hence, AAM is proposed which selects all ABs and OBs as the state vector to establish the registration Equations (16) and (17). As for URM, only OBs remain in the state vector; however, their estimation results include the effects of ABs. URM is preferable for mobile GSP radars because the dependencies between both kinds of biases are strong in this situation. By comparing AAM with URM for UGSP mobile radars, simulation results show that RMSEs of the rectified raw measurements by using AAM bias estimation results are more than 500 m smaller than by URM in all directions. In addition, AAM can obtain the absolute OBs and ABs estimations. So, AAM performs better for mobile UGSP radar registration than URM.
ACKNOWLEDGEMENTS
This work was supported in part by the National Natural Science Foundation of China Grants 61032001, 61102165, 61002006 and the Special Foundation Program for Mountain Tai Scholars of China.
APPENDIX A
DERIVATION OF EQUATION (8)
Using first-order Taylor series expansion about attitude angle measurements, Equations (4)–(6) can be approximated as:
where:
 $${\bf T}_a (k) = \left[ {\matrix{ {c_a} & 0 & { - s_a} \cr 0 & 1 & 0 \cr {s_a} & 0 & {{\rm c}_a} \cr}} \right]$$
$${\bf T}_a (k) = \left[ {\matrix{ {c_a} & 0 & { - s_a} \cr 0 & 1 & 0 \cr {s_a} & 0 & {{\rm c}_a} \cr}} \right]$$ $${\bf T}_a ' (k) = \left[ {\matrix{ { - s_a} & 0 & { - c_a} \cr 0 & 0 & 0 \cr {c_a} & 0 & { - s_a} \cr}} \right] = {\bf T}_a (k)\underbrace {\left[ {\matrix{ 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr}} \right]}_{{\bf R}_a} - \underbrace {\left[ {\matrix{ 0 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}} \right]}_{{\bf R}\prime_a} $$
$${\bf T}_a ' (k) = \left[ {\matrix{ { - s_a} & 0 & { - c_a} \cr 0 & 0 & 0 \cr {c_a} & 0 & { - s_a} \cr}} \right] = {\bf T}_a (k)\underbrace {\left[ {\matrix{ 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr}} \right]}_{{\bf R}_a} - \underbrace {\left[ {\matrix{ 0 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}} \right]}_{{\bf R}\prime_a} $$Substituting Equation (A1)–(A1b) into Equation (7), we obtain
 $${\bf T}_{it\_p2ENU} (k) = \left| \matrix{{\bf T}_{\phi _{it}} (k){\bf T}_{\eta _{it}} (k){\bf T}_{\psi _{it}} (k) \cr \left| \matrix{{\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k) + {\bf T}_{\phi _i} (k){\bf T'}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \eta _i ) \cr {\bf + T'}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \phi _i ) + {\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T'}_{\psi _i} (k)( - \Delta \psi _i ) } \right. \cr = \left| \matrix{\left| \matrix{{\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k) + \cr {\bf T}_{\phi _i} (k)\left( {{\bf T}_{\eta _i} (k)\left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr}} \right] - \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \right]} \right){\bf T}_{\psi _i} (k)( - \Delta \eta _i ) } \right. \cr \quad \quad + \left( {{\bf T}_{\phi _i} (k) - \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 1 \cr}} \right]} \right){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \phi _i ) \cr + {\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k)\left( {{\bf T}_{\psi _i} (k)\left[ {\matrix{ 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr}} \right] - \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}} \right]} \right)( - \Delta \psi _i ) } \right. } \right.$$
$${\bf T}_{it\_p2ENU} (k) = \left| \matrix{{\bf T}_{\phi _{it}} (k){\bf T}_{\eta _{it}} (k){\bf T}_{\psi _{it}} (k) \cr \left| \matrix{{\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k) + {\bf T}_{\phi _i} (k){\bf T'}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \eta _i ) \cr {\bf + T'}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \phi _i ) + {\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T'}_{\psi _i} (k)( - \Delta \psi _i ) } \right. \cr = \left| \matrix{\left| \matrix{{\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k) + \cr {\bf T}_{\phi _i} (k)\left( {{\bf T}_{\eta _i} (k)\left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr}} \right] - \left[ {\matrix{ 1 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 0 \cr}} \right]} \right){\bf T}_{\psi _i} (k)( - \Delta \eta _i ) } \right. \cr \quad \quad + \left( {{\bf T}_{\phi _i} (k) - \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 0 & 0 \cr 0 & 0 & 1 \cr}} \right]} \right){\bf T}_{\eta _i} (k){\bf T}_{\psi _i} (k)( - \Delta \phi _i ) \cr + {\bf T}_{\phi _i} (k){\bf T}_{\eta _i} (k)\left( {{\bf T}_{\psi _i} (k)\left[ {\matrix{ 0 & 0 & { - 1} \cr 0 & 1 & 0 \cr 1 & 0 & 0 \cr}} \right] - \left[ {\matrix{ 0 & 0 & 0 \cr 0 & 1 & 0 \cr 0 & 0 & 0 \cr}} \right]} \right)( - \Delta \psi _i ) } \right. } \right.$$Equation (A2) can be further written as
where the time argument “k” is omitted for simplicity, and
 $${\bf \Delta} _i = \left[ {\matrix{ 0 & {{\rm \Delta \Phi}} & { - {\rm \Delta \Psi}} \cr {\underbrace { - {\rm \Delta \Phi}} _{s_{\psi _i} {\rm \Delta} \eta _i + c_{\eta _i} c_{\psi _i} {\rm \Delta} \phi _i}} & 0 & { - {\rm \Delta \Pi}} \cr {\underbrace {{\rm \Delta \Psi}} _{ - s_{\eta _i} {\rm \Delta} \phi _i - {\rm \Delta} \psi _i}} & {\underbrace {{\rm \Delta \Pi}} _{ - c_{\psi _i} {\rm \Delta} \eta _i + c_{\eta _i} s_{\psi _i} {\rm \Delta} \phi_i}} & 0 \cr}} \right]$$
$${\bf \Delta} _i = \left[ {\matrix{ 0 & {{\rm \Delta \Phi}} & { - {\rm \Delta \Psi}} \cr {\underbrace { - {\rm \Delta \Phi}} _{s_{\psi _i} {\rm \Delta} \eta _i + c_{\eta _i} c_{\psi _i} {\rm \Delta} \phi _i}} & 0 & { - {\rm \Delta \Pi}} \cr {\underbrace {{\rm \Delta \Psi}} _{ - s_{\eta _i} {\rm \Delta} \phi _i - {\rm \Delta} \psi _i}} & {\underbrace {{\rm \Delta \Pi}} _{ - c_{\psi _i} {\rm \Delta} \eta _i + c_{\eta _i} s_{\psi _i} {\rm \Delta} \phi_i}} & 0 \cr}} \right]$$Equation (A3) manifests that the influences of ABs on radar measurements are correlated with TAAs of the platform. These correlations are insulated in mobile GSP radar.
APPENDIX B
DERIVATIONS OF STATE EQUATION OF URM
The difference operator at observation time k+1 can be defined as
According to the definition of Equation (B1), we have:
 $$d_{k + 1} (x_k y_k ) = \left| {\matrix{ {x_{k + 1} y_{k + 1} - x_k y_k =} \cr {x_{k + 1} (y_{k + 1} - y_k ) + x_{k + 1} y_k - x_k y_k =} \cr {x_{k + 1} (y_{k + 1} - y_k ) + y_k (x_{k + 1} - x_k ) =} \cr} x_{k + 1} d_{k + 1} (y_k ) + y_k d_{k + 1} (x_k )} \right.$$
$$d_{k + 1} (x_k y_k ) = \left| {\matrix{ {x_{k + 1} y_{k + 1} - x_k y_k =} \cr {x_{k + 1} (y_{k + 1} - y_k ) + x_{k + 1} y_k - x_k y_k =} \cr {x_{k + 1} (y_{k + 1} - y_k ) + y_k (x_{k + 1} - x_k ) =} \cr} x_{k + 1} d_{k + 1} (y_k ) + y_k d_{k + 1} (x_k )} \right.$$ $$ d_{k + 1} (x_k y_k ) = \left| {\matrix{ {x_{k + 1} y_{k + 1} - x_k y_k =} \cr {x_k (y_{k + 1} - y_k ) - x_k y_{k + 1} + x_{k + 1} y_{k + 1}= x_k d_{k + 1} (y_k ) + y_{k + 1} d_{k + 1} (x_k )} \cr {x_k (y_{k + 1} - y_k ) + y_{k + 1} (x_{k + 1} - x_k ) =} \cr}} \right. $$
$$ d_{k + 1} (x_k y_k ) = \left| {\matrix{ {x_{k + 1} y_{k + 1} - x_k y_k =} \cr {x_k (y_{k + 1} - y_k ) - x_k y_{k + 1} + x_{k + 1} y_{k + 1}= x_k d_{k + 1} (y_k ) + y_{k + 1} d_{k + 1} (x_k )} \cr {x_k (y_{k + 1} - y_k ) + y_{k + 1} (x_{k + 1} - x_k ) =} \cr}} \right. $$Then, the difference of Equation (21) can be written as:
 $$a_{1,k} = \underbrace {\displaystyle{{y_k z_k} \over {x_k^2 + y_k^2}}} _{\alpha _{1,k}} = - d_{k + 1} (\alpha _{1,k} );\ r_k^2 = x_k^2 + y_k^2 ;\ \alpha _k^2 = \displaystyle{{x_k z_k} \over {x_k^2 + y_k^2}} $$
$$a_{1,k} = \underbrace {\displaystyle{{y_k z_k} \over {x_k^2 + y_k^2}}} _{\alpha _{1,k}} = - d_{k + 1} (\alpha _{1,k} );\ r_k^2 = x_k^2 + y_k^2 ;\ \alpha _k^2 = \displaystyle{{x_k z_k} \over {x_k^2 + y_k^2}} $$where [f(x)]k denotes x takes the value of time k. Assuming that the target is moving with constant velocity model from observation time k to k+1, its velocities in x, y, and z directions can be denoted as: v x, vy, vz, respectively, and
![]() $v_{i,k + 1} = {\textstyle{{i_{k + 1} - i_k} \over T}}$; (i={x, y, z}; T denotes the sampling period); then according to Equation (B2), expanding all the difference operators in Equation (B4), Equation (B4) can be rewritten further as:
$v_{i,k + 1} = {\textstyle{{i_{k + 1} - i_k} \over T}}$; (i={x, y, z}; T denotes the sampling period); then according to Equation (B2), expanding all the difference operators in Equation (B4), Equation (B4) can be rewritten further as:
 $$b_{1,k} = - \underbrace {\left[ {\displaystyle{{v_{y,(k + 1)} z_{k + 1} + y_{k + 1} v_{z,(k + 1)}} \over {r_{k + 1}^2}} - \displaystyle{{2x_k y_{k + 1} z_{k + 1} v_{x,(k + 1)} + 2y_{k + 1}^2 z_{k + 1} v_{y,(k + 1)}} \over {r_{k + 1}^4}}} \right]}_{\beta _{1,k + 1}} T$$
$$b_{1,k} = - \underbrace {\left[ {\displaystyle{{v_{y,(k + 1)} z_{k + 1} + y_{k + 1} v_{z,(k + 1)}} \over {r_{k + 1}^2}} - \displaystyle{{2x_k y_{k + 1} z_{k + 1} v_{x,(k + 1)} + 2y_{k + 1}^2 z_{k + 1} v_{y,(k + 1)}} \over {r_{k + 1}^4}}} \right]}_{\beta _{1,k + 1}} T$$ $$\beta _{k + 1}^2 = \displaystyle{{v_{x,(k + 1)} z_{k + 1} + x_{k + 1} v_{z,(k + 1)}} \over {r_{k + 1}^2}} - \displaystyle{{2x_{k + 1}^2 z_{k + 1} v_{x,(k + 1)} + 2x_k y_{k + 1} z_{k + 1} v_{y,(k + 1)}} \over {r_{k + 1}^4}} $$
$$\beta _{k + 1}^2 = \displaystyle{{v_{x,(k + 1)} z_{k + 1} + x_{k + 1} v_{z,(k + 1)}} \over {r_{k + 1}^2}} - \displaystyle{{2x_{k + 1}^2 z_{k + 1} v_{x,(k + 1)} + 2x_k y_{k + 1} z_{k + 1} v_{y,(k + 1)}} \over {r_{k + 1}^4}} $$ $$b_{2,k} = \left| {\matrix{ {\cos \eta _{k + 1} \cos \psi _{k + 1} - \cos \eta _k \cos \psi _k - (\sin \eta _{k + 1} - \sin \eta _k )\alpha _{k + 1}^1} \cr { - (\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )\alpha _{k + 1}^2} \cr { - \beta _{1,k + 1} T\sin \eta _k - \beta _{2,k + 1} T\cos \eta _k \sin \psi _k} \cr}} \right.$$
$$b_{2,k} = \left| {\matrix{ {\cos \eta _{k + 1} \cos \psi _{k + 1} - \cos \eta _k \cos \psi _k - (\sin \eta _{k + 1} - \sin \eta _k )\alpha _{k + 1}^1} \cr { - (\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )\alpha _{k + 1}^2} \cr { - \beta _{1,k + 1} T\sin \eta _k - \beta _{2,k + 1} T\cos \eta _k \sin \psi _k} \cr}} \right.$$ According to Equation (B5), the expectation of d k+1(Δθ′c,k) is not zero. However, it can be viewed as zero-mean Gaussian white noise when we cannot know it exactly, because though the true magnitudes of ABs are not known, they are small. In this situation, the covariances of the equivalent radar angle biases should be increased to ensure the stability of KF. Assuming that the amplitudes of pitch and roll are η max and ψ max, respectively, which can be known in reality, and the target velocities in x, y, and z directions of both radars' local ENU frame have zero-mean Gaussian distributions with their standard derivations are
![]() $\sigma _{v_x} $,
$\sigma _{v_x} $,
![]() $\sigma _{v_y} $ and
$\sigma _{v_y} $ and
![]() $\sigma _{v_z} $, respectively, and also assuming that the target velocity vectors in different radar's ENU frame are independent. Then, Equation (B5) can be written further as
$\sigma _{v_z} $, respectively, and also assuming that the target velocity vectors in different radar's ENU frame are independent. Then, Equation (B5) can be written further as
 $$e_{1,k + 1} = \underbrace {\left[ {\displaystyle{{z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2 + y_{k + 1}^2 \sigma _{v_{z,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{4x_{k + 1}^2 y_{k + 1}^2 z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + 4y_{k + 1}^4 z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^4}}} \right]}_{\gamma _{1,k + 1}} T^2 $$
$$e_{1,k + 1} = \underbrace {\left[ {\displaystyle{{z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2 + y_{k + 1}^2 \sigma _{v_{z,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{4x_{k + 1}^2 y_{k + 1}^2 z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + 4y_{k + 1}^4 z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^4}}} \right]}_{\gamma _{1,k + 1}} T^2 $$ $$\gamma _{2,k + 1} = \displaystyle{{z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + x_{k + 1}^2 \sigma _{v_{z,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{4x_{k + 1}^4 z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + 4x_{k + 1}^2 y_{k + 1}^2 z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^4}} $$
$$\gamma _{2,k + 1} = \displaystyle{{z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + x_{k + 1}^2 \sigma _{v_{z,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{4x_{k + 1}^4 z_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 + 4x_{k + 1}^2 y_{k + 1}^2 z_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^4}} $$where D{x} denotes the variance of x, and E{x} denotes the expectation of x.
Similarly, for elevation bias, according to Equation (22), we have
 $$f_{3,k + 1} = \left| {\matrix{ {\displaystyle{{(\sin \eta _{k + 1} - \sin \eta _k )x_{k + 1}} \over {r_{k + 1}}} + \sin \eta _k d_{k + 1} \left( {\displaystyle{{x_k} \over {r_k}}} \right)} \cr { - \displaystyle{{(\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )y_{k + 1}} \over {r_{k + 1}}} - \cos \eta _k \sin \psi _k d_{k + 1} \left( {\displaystyle{{y_k} \over {r_k}}} \right)} \cr}} \right.$$
$$f_{3,k + 1} = \left| {\matrix{ {\displaystyle{{(\sin \eta _{k + 1} - \sin \eta _k )x_{k + 1}} \over {r_{k + 1}}} + \sin \eta _k d_{k + 1} \left( {\displaystyle{{x_k} \over {r_k}}} \right)} \cr { - \displaystyle{{(\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )y_{k + 1}} \over {r_{k + 1}}} - \cos \eta _k \sin \psi _k d_{k + 1} \left( {\displaystyle{{y_k} \over {r_k}}} \right)} \cr}} \right.$$The further expansion of Equation (B7) can be written as:
 $$ {\tf="P4725F6" g}_{1,k + 1} = \underbrace {\left[ {\displaystyle{{v_{x,k + 1}} \over {r_{k + 1}}} - \displaystyle{{x_{k + 1}^2 v_{x,k + 1} + x_{k + 1} y_{k + 1} v_{y,k + 1}} \over {r_{k + 1}^3}}} \right]}_{\delta _{1,k + 1}} T$$
$$ {\tf="P4725F6" g}_{1,k + 1} = \underbrace {\left[ {\displaystyle{{v_{x,k + 1}} \over {r_{k + 1}}} - \displaystyle{{x_{k + 1}^2 v_{x,k + 1} + x_{k + 1} y_{k + 1} v_{y,k + 1}} \over {r_{k + 1}^3}}} \right]}_{\delta _{1,k + 1}} T$$ $$\delta _{2,k + 1} = \displaystyle{{v_{y,k + 1}} \over {r_{k + 1}}} - \displaystyle{{y_{k + 1}^2 v_{y,k + 1} + x_{k + 1} y_{k + 1} v_{x,k + 1}} \over {r_{k + 1}^3}} $$
$$\delta _{2,k + 1} = \displaystyle{{v_{y,k + 1}} \over {r_{k + 1}}} - \displaystyle{{y_{k + 1}^2 v_{y,k + 1} + x_{k + 1} y_{k + 1} v_{x,k + 1}} \over {r_{k + 1}^3}} $$ $${\tf="P4725F6" g}_{3,k + 1} = \left| {\matrix{ {\displaystyle{{(\sin \eta _{k + 1} - \sin \eta _k )x_{k + 1} - (\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )y_{k + 1}} \over {r_{k + 1}}}} \cr { + \delta _{1,k + 1} T\sin \eta _k - \delta _{2,k + 1} T\cos \eta _k \sin \psi _k} \cr}} \right.$$
$${\tf="P4725F6" g}_{3,k + 1} = \left| {\matrix{ {\displaystyle{{(\sin \eta _{k + 1} - \sin \eta _k )x_{k + 1} - (\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k )y_{k + 1}} \over {r_{k + 1}}}} \cr { + \delta _{1,k + 1} T\sin \eta _k - \delta _{2,k + 1} T\cos \eta _k \sin \psi _k} \cr}} \right.$$Then, the variance can be written as:
 $$i_{1,k + 1} = \underbrace {\left[ {\displaystyle{{\sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{x_{k + 1}^4 \sigma _{v_{x,k + 1}} ^2 + x_{k + 1}^2 y_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^6}}} \right]}_{\mu _{1,k}} T^2 $$
$$i_{1,k + 1} = \underbrace {\left[ {\displaystyle{{\sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{x_{k + 1}^4 \sigma _{v_{x,k + 1}} ^2 + x_{k + 1}^2 y_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^6}}} \right]}_{\mu _{1,k}} T^2 $$ $$i_{2,k + 1} = \underbrace {\left[ {\displaystyle{{\sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{x_{k + 1}^4 \sigma _{v_{y,k + 1}} ^2 + x_{k + 1}^2 y_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^6}}} \right]}_{\mu _{2,k}} T^2 \left| {\cos \psi _k} \right|^2 $$
$$i_{2,k + 1} = \underbrace {\left[ {\displaystyle{{\sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^2}} + \displaystyle{{x_{k + 1}^4 \sigma _{v_{y,k + 1}} ^2 + x_{k + 1}^2 y_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^6}}} \right]}_{\mu _{2,k}} T^2 \left| {\cos \psi _k} \right|^2 $$Next, the covariance of the azimuth and elevation biases can be computed as:
 $$ \sigma _{d_{k + 1} (\Delta \theta _k' )d_{k + 1} (\Delta \varepsilon _k' )}^2 = \left| {\matrix{ {\sigma _{\Delta \theta \hskip 1pt' \Delta \varepsilon '} ^2 =} \cr {E\{ d_{k + 1} (\Delta \theta _k ' )d_{k + 1} (\Delta \varepsilon _k' )\}} \cr}} \right. \leqslant \left| {\matrix{ {\matrix{ {n_{1,k + 1} (\Delta \psi _k )^2 + n_{2,k + 1} (\Delta \eta _k )^2 +} \cr {n_{3,k + 1} (\Delta \phi _k )^2 + n_{4k + 1} \Delta \psi _k \Delta \eta _k} \cr}} \cr { + n_{5,k + 1} \Delta \phi _k \Delta \psi _k + n_{6,k + 1} \Delta \phi \Delta \eta} \cr}} \right.$$
$$ \sigma _{d_{k + 1} (\Delta \theta _k' )d_{k + 1} (\Delta \varepsilon _k' )}^2 = \left| {\matrix{ {\sigma _{\Delta \theta \hskip 1pt' \Delta \varepsilon '} ^2 =} \cr {E\{ d_{k + 1} (\Delta \theta _k ' )d_{k + 1} (\Delta \varepsilon _k' )\}} \cr}} \right. \leqslant \left| {\matrix{ {\matrix{ {n_{1,k + 1} (\Delta \psi _k )^2 + n_{2,k + 1} (\Delta \eta _k )^2 +} \cr {n_{3,k + 1} (\Delta \phi _k )^2 + n_{4k + 1} \Delta \psi _k \Delta \eta _k} \cr}} \cr { + n_{5,k + 1} \Delta \phi _k \Delta \psi _k + n_{6,k + 1} \Delta \phi \Delta \eta} \cr}} \right.$$ $$j_{1,k + 1} = \left| {\sin \psi _{k + 1} - \sin \psi _k} \right| + \displaystyle{{\left| {\cos \psi _{k + 1} - \cos \psi _k} \right|x_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}} $$
$$j_{1,k + 1} = \left| {\sin \psi _{k + 1} - \sin \psi _k} \right| + \displaystyle{{\left| {\cos \psi _{k + 1} - \cos \psi _k} \right|x_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}} $$ $$j_{2,k + 1} = \left| {\matrix{ {\left| {\cos \eta _{k + 1} \cos \psi _{k + 1} - \cos \eta _k \cos \psi _k} \right| + \displaystyle{{\left| {\sin \eta _{k + 1} - \sin \eta _k} \right|y_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}}} \cr { + \displaystyle{{\left| {\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k} \right|x_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}}} \cr}} \right.$$
$$j_{2,k + 1} = \left| {\matrix{ {\left| {\cos \eta _{k + 1} \cos \psi _{k + 1} - \cos \eta _k \cos \psi _k} \right| + \displaystyle{{\left| {\sin \eta _{k + 1} - \sin \eta _k} \right|y_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}}} \cr { + \displaystyle{{\left| {\cos \eta _{k + 1} \sin \psi _{k + 1} - \cos \eta _k \sin \psi _k} \right|x_{k + 1} z_{k + 1}} \over {r_{k + 1}^2}}} \cr}} \right.$$ $$m_{1,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{z_{k + 1} (\sigma _{v_{x,k + 1}} ^2 - \sigma _{v_{y,k + 1}} ^2 )} \over {r_{k + 1}^3}} + \displaystyle{{3z_{k + 1} (y_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2 - x_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 )} \over {r_{k + 1}^5}}} \cr { - \displaystyle{{2z_{k + 1} \left[ {(x_{k + 1}^4 - x_{k + 1}^2 y_{k + 1}^2 )\sigma _{v_x} ^2 + (x_{k + 1}^2 y_{k + 1}^2 - y_{k + 1}^4 )\sigma _{v_y} ^2} \right]} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{1,k}} T^2 \left| {\sin \eta _k} \right|\left| {\cos \psi _k} \right| $$
$$m_{1,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{z_{k + 1} (\sigma _{v_{x,k + 1}} ^2 - \sigma _{v_{y,k + 1}} ^2 )} \over {r_{k + 1}^3}} + \displaystyle{{3z_{k + 1} (y_{k + 1}^2 \sigma _{v_{y,k + 1}} ^2 - x_{k + 1}^2 \sigma _{v_{x,k + 1}} ^2 )} \over {r_{k + 1}^5}}} \cr { - \displaystyle{{2z_{k + 1} \left[ {(x_{k + 1}^4 - x_{k + 1}^2 y_{k + 1}^2 )\sigma _{v_x} ^2 + (x_{k + 1}^2 y_{k + 1}^2 - y_{k + 1}^4 )\sigma _{v_y} ^2} \right]} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{1,k}} T^2 \left| {\sin \eta _k} \right|\left| {\cos \psi _k} \right| $$ $$m_{5,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{ - 2x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{y,k + 1}} ^2 - x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^5}}} \cr { + \displaystyle{{2x_{k + 1}^3 y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2 + 2x_{k + 1} y_{k + 1}^3 z_{k + 1} \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{2,k}} T^2 \left| {\cos \psi _k} \right|^2 $$
$$m_{5,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{ - 2x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{y,k + 1}} ^2 - x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^5}}} \cr { + \displaystyle{{2x_{k + 1}^3 y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2 + 2x_{k + 1} y_{k + 1}^3 z_{k + 1} \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{2,k}} T^2 \left| {\cos \psi _k} \right|^2 $$ $$m_{8,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{y,k + 1}} ^2 + 2x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^5}}} \cr { - \displaystyle{{2x_{k + 1}^3 y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2 + 2x_{k + 1} y_{k + 1}^3 z_{k + 1} \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{3,k}} T^2 \left| {\sin \eta _k} \right|^2 $$
$$m_{8,k + 1} = \underbrace {\left[ {\matrix{ {\displaystyle{{x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{y,k + 1}} ^2 + 2x_{k + 1} y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2} \over {r_{k + 1}^5}}} \cr { - \displaystyle{{2x_{k + 1}^3 y_{k + 1} z_{k + 1} \sigma _{v_{x,k + 1}} ^2 + 2x_{k + 1} y_{k + 1}^3 z_{k + 1} \sigma _{v_{y,k + 1}} ^2} \over {r_{k + 1}^7}}} \cr}} \right]}_{\zeta _{3,k}} T^2 \left| {\sin \eta _k} \right|^2 $$The computation of the covariances in Equations (B6), (B9), and (B10) we need to know the true magnitudes of ABs. However, if they cannot be known in advance, their possible maximum values can be used to substitute for their true values.