Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T01:42:55.645Z Has data issue: false hasContentIssue false
  • English
  • Français

The cocked hat: formal statements and proofs of the theorems

Published online by Cambridge University Press:  15 February 2021

Imre Bárány ,
William Steiger  and
Sivan Toledo Open the ORCID record for Sivan Toledo [Opens in a new window]
Imre Bárány
Affiliation:
Rényi Institute of Mathematics, 13–15 Reáltanoda Street, Budapest1053Hungary. Department of Mathematics, University College London, Gower Street, LondonWC1E 6BT, UK.
William Steiger
Affiliation:
Department of Computer Science, Rutgers University, 110 Frelinghuysen Road, Piscataway, NJ08854-8019, USA.
Sivan Toledo*
Affiliation:
Blavatnik School of Computer Science, Tel Aviv University, Tel Aviv6997801, Israel
*
*Corresponding author. E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Navigators have been taught for centuries to estimate the location of their craft on a map from three lines of position, for redundancy. The three lines typically form a triangle, called a cocked hat. How is the location of the craft related to the triangle? For more than 80 years navigators have also been taught that, if each line of position is equally likely to pass to the right and to the left of the true location, then the likelihood that the craft is in the triangle is exactly 1/4. This is stated in numerous reputable sources, but was never stated or proved in a mathematically formal and rigorous fashion. In this paper we prove that the likelihood is indeed 1/4 if we assume that the lines of position always intersect pairwise. We also show that the result does not hold under weaker (and more reasonable) assumptions, and we prove a generalisation to 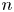$n$ lines.

Keywords

pilotagestochastic errorhistory
Type
Research Article
Information
The Journal of Navigation , Volume 74 , Issue 3 , May 2021 , pp. 713 - 722
Check for updates
Copyright
Copyright © The Royal Institute of Navigation 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, E. W. (1952). The treatment of navigational errors. Journal of Navigation, 5(2), 103–124. doi:10.1017/S0373463300044519CrossRefGoogle Scholar
Charnley, J. (1993). J. E. D. Williams. Journal of Navigation, 46(2), 290–292. An obituary. doi:10.1017/S0373463300011668CrossRefGoogle Scholar
Cook, I. (1993). Random cocked hats. Journal of Navigation, 46(1), 132–135. A response by J. E. D. Williams appears on pages 135–137. doi:10.1017/S0373463300011383CrossRefGoogle Scholar
Cotter, C. H. (1961). The cocked hat. Journal of Navigation, 14(2), 223–230. doi:10.1017/S0373463300039564CrossRefGoogle Scholar
Daniels, H. E. (1951). The theory of position finding. Journal of the Royal Statistical Society, Series B (Methodological), 13(2), 186–207. https://www.jstor.org/stable/2984060CrossRefGoogle Scholar
Dear, I. C. B. and Kemp, P. (2006). The Oxford Companion to Ships and the Sea. 2nd ed. Oxford, UK: Oxford University Press.CrossRefGoogle Scholar
Denny, M. (2012). The Science of Navigation: From Dead Reckoning to GPS. Baltimore, Maryland: The Johns Hopkins University Press.Google Scholar
His Majesty's Navigation School (1938). Admiralty Navigation Manual. Vol. 3. London, UK: His Magesty's Stationary Office.Google Scholar
Stansfield, R. G. (1947). Statistical theory of D.F. fixing. Journal of the Institution of Electrical Engineers Part IIIA: Radiocommunication, 94(5), 762–770. doi:10.1049/ji-3a-2.1947.0096Google Scholar
Stuart, R. G. (2019). Probabilities in a Gaussian cocked hat. Journal of Navigation, 72(6), 1496–1512. doi:10.1017/S0373463319000110CrossRefGoogle Scholar
The Open University (1984). M245 Probability and statistic: Item 15, Findings One's Bearings. A video that is part of course materials. UK. https://www.open.ac.uk/library/digital-archive/video:FOUM190WGoogle Scholar
Williams, J. E. D. (1991). The cocked hat. Journal of Navigation, 44(2), 269–271. doi:10.1017/S0373463300009991CrossRefGoogle Scholar