Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-24T17:02:47.839Z Has data issue: false hasContentIssue false
  • English
  • Français

Deformation Kinetics of Steady Creep in Sn/Pb Solder Alloys With Applications

Published online by Cambridge University Press:  05 May 2011

C. F. Lee ,
M. K. Chang  and
W. K. Chung
C. F. Lee*
Affiliation:
Department of Engineering Science, National Cheng Kung University, Tainan, Taiwan 70101, R.O.C.
M. K. Chang*
Affiliation:
Laser Division, Unity Opto Tech. Co., Taipei County, Taiwan 241, R.O.C.
W. K. Chung*
Affiliation:
Assy/Test Eng. Sec., Nanya Tech. Co., Taoyuan, Taiwan 333, R.O.C.
*
*Professor
*Engineer
*Engineer
Get access

Abstract

In this paper, a constitutive equation of steady creep rates:

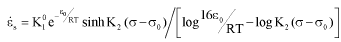
is derived based on a liaison of the theory of irreversible thermodynamics of continuous media with internal state variables (ISV); and the deformation kinetics. In steady creep, only one ISV is used, whose evolution equation is derived by the concepts of deformation kinetics, in which micromotions are generated by a group of atoms climbing over a tilted potential barrier of the highest height ε0.

Applications of the constitutive equation in the cases of some Sn/Pb solder alloys-63Sn/37Pb, 60Sn/40Pb and 97.5Pb/2.5Sn under shear creep tests; and 98Pb/2Sn under tensile creep tests, show that the theoretical results can describe the experimental data quite well. These results pave the way for future research in the comparisons of creep resistance among solders with various Sn/Pb compositions and in the generalization of three-dimensional constitutive equation.

Keywords

Steady creep ratesConstitutive equation, Internal variableDeformation kineticsTilted potential barrierSn/Pb solders
Type
Articles
Information
Journal of Mechanics , Volume 20 , Issue 2 , June 2004 , pp. 85 - 93
Copyright
Copyright © The Society of Theoretical and Applied Mechanics, R.O.C. 2004

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Solomon, H. D., “Predicting Thermal and Mechanical Fatigue Lives from Isothermal Low Cycle Data,” Solder Joint Reliability, Lau, J. H., Van Nostrand, Reinhold, eds., Ch.14, N.Y., U.S.A., pp. 406–454 (1991).CrossRefGoogle Scholar
2.Vaynman, S., Fine, M. E. and Jeannotte, D. A., “Low-Cycle Isothermal Fatique Life of Solder Materials,” Solder Mechanics—A State of the Art Assessment, Frear, D. R., Jones, W. B., and Kinsman, K. R., eds., Ch. 4, The Minerals, Metals & Materials Society, pp. 155–189 (1991).Google Scholar
3.Frost, H. J., Howard, R. T., Lavery, P. R. and Lutender, S. D., “Creep and Tensile Behavior of Lead-Rich, Lead-Tin Solder Alloys,” IEEE Trans. Components, Hybrids, and Manufacturing Technology, 11(4), pp. 371–379 (1988).Google Scholar
4.Morris, J. W. Jr. and Reynolds, H. L., “The Influence of Microstructure on the Mechanics of Eutectic Solders,” ASME EEP, 19(2), Advances in Electronic Packaging, pp. 1529–1534 (1997).Google Scholar
5.Darveaux, R. and Benerji, K., “Constitutive Relations for Tin-Based Solder Joints,” IEEE Trans. Components, Hybirds, and Manufacturing Technology, 15(6), pp. 1013–1024 (1992).CrossRefGoogle Scholar
6.McDowell, D. L., Miller, M. P. and Brooks, D. C., “A Unified Creep-Plasticity Theory for Solder Alloys,” Fatigue of Electronic Materials, eds., Schroeder, S. A. and Mitchell, M. R., ASTM STP 1153, pp. 42–59(1994).CrossRefGoogle Scholar
7.Maciucescu, L., Sham, T. L. and Krempl, E., “VBO: A State Variable Constitutive Equation for a Solder Alloy,” ASME EEP., 19(2), Advance in Electronic Packaging, pp. 1615–1621 (1997).Google Scholar
8.Rassaian, M., Desai, C. S., Whitenack, R. and Lee, J. C., “A Unified Constitutive Model Based on Distributed State Concept and Multi-Domain Method for Design and Reliability in Electronic Packaging,” ASME EEP., 26(6), Advances in Electronic Packaging, pp. 2031–2036 (1999).Google Scholar
9.Sasaki, K., Ohguchi, K-I. and Ishikawa, H., “Viscoplastic Deformation of 40Pb/60Sn Solder Alloys—Experiments and Constitutive Modeling,” J. Electronic Packaging, ASME, pp. 379–387 (2001).Google Scholar
10.Valanis, K. C. and Lalwani, S. A., “Thermodynamics of Internal Variables in the Context of Absolute Reaction Rate Theory,” J. Chm. Phys., 67, pp. 3980–3990 (1997).Google Scholar
11.Valanis, K. C. and Lee, C. F., “Deformation Kinetics of Steady-State Creep in Metals,” Int. J. Solids Structures, 17, pp. 589–604 (1981).CrossRefGoogle Scholar
12.Krausz, A. S. and Eyring, H., Deformation Kinetics, Wiley, New York (1975).Google Scholar
13.Valanis, K. C., Irrreversible Thermodynamics of Continuous Media-Internal Variable Theory, Springer-Verlag, New York (1972).Google Scholar
14.Shi, X.Q., Yang, Q.J., Wang, Z. P., Pang, H.L.J. and Zhou, W., “Reliability Assessment of PGBA Solder Joints Using the New Creep Contitutive Relationship and Modified Energy-Based Life Prediction Model,” IEEE Electronic Components and Technology Conterence, 3(5–7), Dec., pp. 398–405 (2000).Google Scholar