Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-26T13:01:13.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Theory of Endochronic Cyclic Viscoplasticity of Eutectic Tin/Lead Solder Alloy

Published online by Cambridge University Press:  05 May 2011

C. F. Lee  and
T. J. Shieh
C. F. Lee*
Affiliation:
Department of Engineering Science, College of Engineering, National Cheng-Kung University, Tainan, Taiwan 70101, R.O.C.
T. J. Shieh*
Affiliation:
CF MFG. Division 4, CF Testing Department, Chi-Mei Optoelectronic Co.
*
*Professor
**Engineer
Get access

Abstract

In this paper, a theory of Endochronic cyclic viscoplasticity of eutectic Tin/Lead (60Sn/40Pb) solder alloy under cyclically thermomechanical strain histories had been established. Under the conditions of isotropic and inelastically incompressible small deformation, the constitutive equation of deviatoric behavior was expressed as:

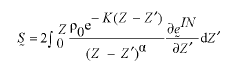
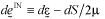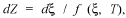
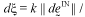
here and the strain rate dependent intrinsic time scale and 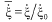. Employing the experimental cyclic shear stress-strain curves of various testing temperature and frequency, all temp. dependent material parameters and 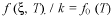; and the temp.-freq. dependent material function were determined for temp. between 213K and 423K and freq. between 0.3Hz and 0.01Hz. Predicative capability of the theory were then challenged by a set of experiments with complicate strain history such as (i) Fast in tension/Slow in compression constant strain amplitude cyclic tests (ii) Slow-Fast-Slow constant amplitude cyclic tests. Through the excellent computational results, the present theory demonstrated that it can, not only play a vital role in the area of electronic solder mechanics, but also meet the needs of reliability analysis and life assessment in the electronic/photoelectronic packagings.

Keywords

Endochronic viscoplasticity60Sn/40PbStrain rate dependent intrinsic time scaleElectronic solder mechanics.
Type
Articles
Information
Journal of Mechanics , Volume 22 , Issue 3 , September 2006 , pp. 181 - 191
Copyright
Copyright © The Society of Theoretical and Applied Mechanics, R.O.C. 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Knecht, S. and Fox, L. R., “Constitutive Relation and Creep-Fatigue Life Model for Eutectic Tin-Lead Solder,” IEEE Trans. Comp. Hybrids, Manuf. Technol. 13, pp. 424–433 (1990).Google Scholar
2.Mc Dowell, D. L., Miller, M. P. and Brooks, D. C., “A Unified Creep-Plasticity Theory for Solder Alloys,” Fatigue of Electronic Materials, Schroder, S. A. and Mitchell, M. R., Eds., ASTMSTP1153, pp. 42–59 (1994).Google Scholar
3.Maciucescu, L., Sham, T. L. and Krempl, E., “VBO: A State Variable Constitutive Eqation for a Solder Alloy,” ASME EEP. Advances in Electronic Packaging, 19–2, pp. 1615–1621 (1997).Google Scholar
4.Rassaian, M., Desai, C. S., Whitenack, R. and Lee, J. C., “A Unified Constitutive Model Based on Distributed State Concept and Multi-Domain Method for Design and Reliability in Electronic Packaging,” ASME EEP. Advances in Electronic Packaging, 26–6, pp. 2031–2036 (1999).Google Scholar
5.Ishikawa, H., Sasaki, K. and Ohguchi, K., “Prediction of Fatigue Failure of 60Sn–40Pb Solder – Using Constitutive Model for Cyclic Viscoplasticity,” ASME J. Electron. Packag., 118, pp. 164–169(1996).Google Scholar
6.Busso, E. P., Kitano, M. and Kumazawa, T., “A Visco-Plastic Constitutive Model for 60/40 Tin-Lead Solder Used in IC Package Joints,” ASME J. Engnr. Materials and Technology, 114, pp. 331–337(1992).Google Scholar
7.Sasaki., K., Ohguchi, K-I. and Ishikawa, H., “Viscoplastic Deformation of 40Pb/60Sn Solder Alloys-Experiments and Constitutive Modeling,” ASME J. Electron. Packag., pp. 379–387(2001).Google Scholar
8.Valanis, K. C., “A Theory of Viscoplasticity Without a Yield Surface, Part I, General Theory, Part II Application to Mechanical Behavior of Metals,” Arch. Mech., 23, pp. 517–551 (1971).Google Scholar
9.Valanis, K. C. and Lee, C. F., “Endochronic Theory of Cyclic Plasticity with Applications,” ASME J. Appl. Mech., 51, pp. 367–374 (1984).Google Scholar
10.Valanis, K. C. and Read, H. E., A New Endochronic Plasticity Model for Soil Mechanics - Transient and Cyclic Loads John Wiley & S ons Ltd., pp. 375–417 (1982).Google Scholar
11.Valanis, K. C., Read, H. E., “An Endochronic Plasticity Theory for Concrete,” Mech. Mater., 5, pp. 177–295 (1986).Google Scholar
12.Lee, C. F., “Recent Finite Element Applications of the Incremental Endochronic Plasticity,” Int. J. Plasticity, 11, pp. 843–865 (1995).Google Scholar
13.Lee, C. F., “EndoFEM Integrated Methodology of Fatigue Crack Propagation with Overloaded Delay Retardation,” The Chinese J. Mechanics, 19(2), pp. 327–335 (2003).Google Scholar
14.Lee, C. F., Shen, H. T. and Peng, W. T., “A Unified Creep-Cyclic Plasticity Theory of Endochronic Viscoplasticity with Applications in 304 Stainless Steel,” The Chinese J. Mechanics, 19(4), pp. 443–453 (2003).Google Scholar
15.Lee, C. F., “A Simple Endochronic Transient Creep Model of Metals with Applications to Variable Temperature Creep,” Int. J. Plasticity, 12, pp. 239–253 (1996).Google Scholar
16.Otsuka, K. and Usa, M., Semiconductor Packaging Engineerin, Fig. 10.4, Nikkei Business Publications. Inc. Japan, p. 172(1997).Google Scholar
17.Lee, C. F., “A Systematic Method of Determining Material Function in the Endochronic Plasticity,” J. Chinese Soc. Mech. Engng 8, pp. 419–430 (1987).Google Scholar
18.Vaynman, S., Fine, M. E. and Jeannotte, D. A., “Low-Cycle Isothermal Fatigue Life of Solder Materials,” Solder Mechanics —A State of the Art Assessment, Frear, D. R., Jones, W. B. and Kinsman, K. R., Eds., The Minearls, Metals & Materials Society (1991).Google Scholar
19.Solomon, H. D., “Predicting Thermal and Mechanical Fatigue Lives from Isothermal Low Cycle Data,” Solder Joint Reliability Lau, J. H., Van Nostrand, Reinhold, Eds., N.Y. (1991).Google Scholar
20.Darveaux, R. and Banerji, K., “Constitutive Relation for Tin-Based Solder Joint,” IEEE Tran. Comp., Hybrid, Manuf. Technol. 15. pp. 1013–1024 (1992).Google Scholar
21.Manson, S. S., “Fatigue at Elevated Temperature,” ASTM STP1973 520, pp. 744–782 (1973).Google Scholar