Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T12:01:28.889Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermodynamics of ZnxMn3−xO4 and Mg1−zCuzCr2O4 spinel solid solutions

Published online by Cambridge University Press:  17 June 2019

Kristina Lilova ,
Geetu Sharma ,
Shmuel Hayun ,
Daniel P. Shoemaker  and
Alexandra Navrotsky
Kristina Lilova
Affiliation:
Peter A. Rock Thermochemistry Laboratory and NEAT ORU, University of California Davis, Davis, California 95616, USA
Geetu Sharma
Affiliation:
Peter A. Rock Thermochemistry Laboratory and NEAT ORU, University of California Davis, Davis, California 95616, USA
Shmuel Hayun
Affiliation:
Peter A. Rock Thermochemistry Laboratory and NEAT ORU, University of California Davis, Davis, California 95616, USA; and Department of Materials Engineering, Ben Gurion University of the Negev, Beer-Sheva 84105, Israel
Daniel P. Shoemaker
Affiliation:
Materials Department and Materials Research Laboratory, University of California, Santa Barbara, California 93106, USA
Alexandra Navrotsky*
Affiliation:
Peter A. Rock Thermochemistry Laboratory and NEAT ORU, University of California Davis, Davis, California 95616, USA
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

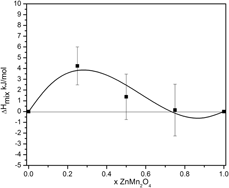
The thermodynamic properties of ZnxMn3−xO4 and Mg1−zCuzCr2O4 spinel solid solutions have been studied using high-temperature oxide melt solution calorimetry. Except for MgCr2O4 spinel, which possesses cubic structure, the other three end-members are tetragonal. The enthalpies of mixing are small endothermic and fit subregular solution behavior. The main contribution to the energetics of mixing of both spinel systems comes from the difference in the crystal structure between the end-members: a change in the tetragonal distortion for ZnxMn3−xO4 solid solutions and a transition from cubic to tetragonal for the Mg1−zCuzCr2O4 system. If all Mg1−zCuzCr2O4 spinels possessed the same structure, the mixing enthalpies would be close to zero. Because both series have normal cation distributions, the entropies of mixing are equal to the configurational entropies of mixing of Zn2+ and Mn2+ and of Mg2+ and Cu2+ on tetrahedral sites, and the activities would follow Raoult’s law. The calculated Gibbs energy of mixing confirms the absence of solvus at any temperature for both systems.

Keywords

calorimetrycrystallographic structuregeologic
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 19: Focus Issue: Thermodynamics of Complex Solids , 14 October 2019 , pp. 3305 - 3311
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

b)

Present address: Materials Science and Engineering Department, University of Illinois, Urbana, Illinois 61801, USA.

c)

This author was an editor of this journal during the review and decision stage. For the JMR policy on review and publication of manuscripts authored by editors, please refer to http://www.mrs.org/editor-manuscripts/.

References

Severino, F., Brito, J., Carias, O., and Laine, J.: Comparative study of alumina-supported CuO and CuCr2O4 as catalysts for CO oxidation. J. Catal. 102, 172–179 (1986).CrossRefGoogle Scholar
Meyer, R.: Explosives, 3rd ed. (Wiley-VCH, Weinheim, 1987); p. 285.Google Scholar
West, A.R.: Solid State Chemistry and its Applications (John Wiley & Sons Ltd., Chichester, New York; Brisbane, Toronto, Singapore, 1984); p. 734.Google Scholar
Shen, S., Chen, S., and Wu, B.: The thermal decomposition of ammonium perchlorate (AP) containing a burning-rate modifier. Thermochim. Acta 223, 135–143 (1993).CrossRefGoogle Scholar
Yan, J., Zhang L, L., Yang, H., Tang, Y., Lu, Z., Guo, S., Dai, Y., Han, Y., and Yao, M.: CuCr2O4/TiO2 heterojunction for photocatalytic H2 evolution under simulated sunlight irradiation. J. Sol. Energy 83, 1534–1539 (2009).CrossRefGoogle Scholar
Dandekar, A., Baker, R.T.K., and Vannice, M.A.: Carbon supported copper catalyst: II. Crotonaldehyde hydrogenation. J. Catal. 184, 421–439 (1997).CrossRefGoogle Scholar
Laine, J. and Severino, F.: Changes in alumina-supported copper and copper—Chromite catalysts by the introduction of water during carbon monoxide oxidation. Appl. Catal. 65, 253–258 (1990).CrossRefGoogle Scholar
Guillemet-Fritsch, S., Chanel, C., Sarrias, J., Bayonne, S., Rousset, A., Alcobe, X., and Martinez Sarrion, M.L.: Structure, thermal stability and electrical properties of zinc manganites. Solid State Ionics 128, 233–242 (2000).CrossRefGoogle Scholar
Buchanan, R.C.: Ceramics Materials for Electronics, 3rd ed. (Marcel Dekker, New York, 2004).Google Scholar
Yang, P., Yang, H.Q., Lu, Y.L., Li, N., and Li, B.X.: Research of Zn–Mn spinel electrode materials for aqueous secondary batteries. J. Power Sources 62, 223–227 (1996).Google Scholar
Irvine, T.N.: Chromian spinel as a petrogenetic indicator, part I. Theory. Can. J. Earth Sci. 2, 648–672 (1965).CrossRefGoogle Scholar
Evans, B.W. and Frost, B.R.: Chrome spinels in progressive metamorphism—A preliminary analysis. Geochim. Cosmochim. Acta 39, 959–972 (1975).CrossRefGoogle Scholar
Dick, H.J.B. and Bullen, T.: Chromian spinel as a petrogenetic indicator in abyssal and alpine-type peridotites and spatially associated lavas. Contrib. Mineral. Petrol. 86, 54–76 (1984).CrossRefGoogle Scholar
Sack, R.O. and Ghiorso, M.S.: Chromian spinels as petrogenetic indicators: Thermodynamics and petrological applications. Am. Mineral. 76, 827–847 (1991).Google Scholar
Allan, J.F., Sack, R.O., and Batiza, R.: Cr-rich spinels as petrogenetic indicators: MORB-type lavas from the lamont seamount chain, eastern pacific. Am. Mineral. 73, 741–753 (1988).Google Scholar
Miller, A.: Distribution of cations in spinels. J. Appl. Phys. 30, S24–25S (1959).CrossRefGoogle Scholar
Shoemaker, D.P., Rodriguez, E.E., and Seshadri, R.: Intrinsic exchange bias in ZnxMn3−xO4 (x ≤ 1) solid solutions. Phys. Rev. B 80, 144422–144431 (2009).CrossRefGoogle Scholar
Shoemaker, D.P. and Seshadri, R.: Total scattering descriptions of local and cooperative distortions in the oxide spinel Mg1−xCuxCr2O4 with dilute Jahn–Teller ions. Phys. Rev. B 82, 214107-1–214107-9 (2010).CrossRefGoogle Scholar
Navrotsky, A. and Kleppa, O.J.: Thermodynamics of formation of simple spinels. J. Inorg. Nucl. Chem. 30, 479–498 (1968).CrossRefGoogle Scholar
Muller, F. and Kleppa, O.J.: Thermodynamics of formation of chromite spinels. J. Inorg. Nucl. Chem. 35, 2673–2678 (1973).CrossRefGoogle Scholar
Schmahl, N.G. and Minzl, E.: Ermittlung thermodynamischer Daten von Doppeloxidbildungen aus Gleichgewichtsmessungen. Z. Phys. Chem. 47, 358–382 (1965).CrossRefGoogle Scholar
Gadalla, A.M.M. and White, J.: Equilibrium relationships in the system CuO–Cu2O–Al2O3. Trans. J. Br. Ceram. Soc. 63, 39–62 (1964).Google Scholar
Tretjakow, J.D. and Schmalzried, H.: Zur Thermodynamik von Spinellphasen. (Chromite, Ferrite, Aluminate). Ber. Bunsenges. Phys. Chem. 69, 396–402 (1965).CrossRefGoogle Scholar
Jacob, K.T., Kale, G.M., and Iyengar, G.N.K.: Oxygen potentials, Gibbs’ energies and phase relations in the Cu–Cr–O system. J. Mater. Sci. 21, 2753–2758 (1986).CrossRefGoogle Scholar
Zhang, P., Lee, T., Xu, F., and Navrotsky, A.: Energetics of ZnO nanoneedles: Surface enthalpy, stability, and growth. J. Mater. Res. 23, 1652–1657 (2008).CrossRefGoogle Scholar
Birkner, N. and Navrotsky, A.: Thermodynamics of manganese oxides: Effects of particle size and hydration on oxidation-reduction equilibria among hausmannite, bixbyite, and pyrolusite. Am. Mineral. 97, 1291–1298 (2012).CrossRefGoogle Scholar
Klemme, S. and O’Neill, H.S.C.: The reaction MgCr2O4 + SiO2 = Cr2O3 + MgSiO3 and the free energy of formation of magnesiochromite (MgCr2O4). Contrib. Mineral. Petrol. 130, 59–65 (1997).CrossRefGoogle Scholar
Fritsch, S. and Navrotsky, A.: Thermodynamic properties of manganese oxides. J. Am. Ceram. Soc. 79, 1761–1768 (1996).CrossRefGoogle Scholar
Robie, R.A. and Hemingway, B.S.: Thermodynamic Properties of Minerals and Related Substances at 298.15 K and 1 Bar (105 Pascals) Pressure and at Higher Temperatures (U.S. Geological Survey Bulletin, 2131, Washington DC, 1995); p. 461.Google Scholar
Chase, M.W. Jr., Davies, C.A., Downey, J.R. Jr., Frurip, D.J., Mc-Donald, R.A., and Syverud, A.N.: JANAF thermochemical tables. Third edition. Part II. Cr–Zr. J. Phys. Chem. Ref. Data 14(Suppl. 1), 927–1856 (1985).Google Scholar
Shannon, R.D.: Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A32, 751–767 (1976).CrossRefGoogle Scholar
Yé, Z-G., Crottaz, O., Vaudano, F., Kubel, F., Tissot, P., and Schmid, H.: Single crystal growth, structure refinement, ferroelastic domains and phase transitions of the hausmannite CuCr2O4. Ferroelectrics 162, 103–118 (1994).CrossRefGoogle Scholar
Kennedy, B.J. and Zhou, Q.: The role of orbital ordering in the tetragonal-to-cubic phase transition in CuCr2O4. J. Solid State Chem. 181, 2227–2230 (2008).CrossRefGoogle Scholar
Ehrenberg, H., Knapp, M., Baehtz, C., and Klemme, S.: Tetragonal low-temperature phase of MgCr2O4. Powder Diffr. 17, 230–233 (2002).CrossRefGoogle Scholar
Kemei, M.C., Moffitt, S.L., Shoemaker, D.P., and Seshadri, R.: Evolution of magnetic properties in the normal spinel solid solution Mg1−xCuxCr2O4. J. Phys.: Condens. Matter 24, 042011–046003 (2012).Google Scholar
Navrotsky, A.: Progress and new directions in high temperature calorimetry. Phys. Chem. Miner. 2, 89–104 (1977).CrossRefGoogle Scholar
Navrotsky, A.: Progress and new directions in high-temperature calorimetry revisited. Phys. Chem. Miner. 24, 222–241 (1997).CrossRefGoogle Scholar
Navrotsky, A.: Progress and new directions in calorimetry: A 2014 perspective. J. Am. Ceram. Soc. 97, 3349–3359 (2014).CrossRefGoogle Scholar