Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T00:39:10.780Z Has data issue: false hasContentIssue false
  • English
  • Français

The strain-induced martensitic phase transformation of Fe–C alloys considering C addition: A molecular dynamics study

Published online by Cambridge University Press:  30 June 2020

Ye Jiao ,
WenJiao Dan  and
WeiGang Zhang
Ye Jiao
Affiliation:
Department of Engineering Mechanics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai200240, China
WenJiao Dan*
Affiliation:
Department of Engineering Mechanics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai200240, China
WeiGang Zhang
Affiliation:
Department of Engineering Mechanics, School of Naval Architecture, Ocean and Civil Engineering, Shanghai Jiao Tong University, Shanghai200240, China
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

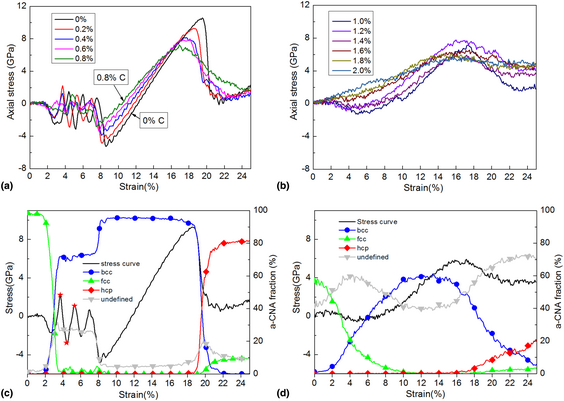
This study investigates the effect of C on the deformation mechanisms in Fe–C alloys by molecular dynamics simulations. In uniaxial tensile simulations, the face-centered-cubic (fcc) structures of Fe–C alloys undergo the following deformation processes: (i) fcc→body-centered-cubic (bcc) martensitic transformation, (ii) deformation of bcc phase, and (iii) bcc→hcp martensitic transformation, which are significantly influenced by the C concentration. For the low C concentrations (0–0.8 wt%) fcc phase, the fcc→bcc phase transformation accords a two-stage shear transformation mechanism based on the Bain model, the deformation mechanism of the bcc phase is the first migration of twinning structures and then elastic deformation, and the bcc→hcp phase transformation follows Burgers relations resulting from the shear of the bcc close-packed layers. However, for the fcc phase with high C concentrations (1.0–2.0 wt%), the fcc→bcc phase transformation follows a localized Bain transformation mechanism impeded by the C atoms, the bcc phase only experiences elastic deformation, and the bcc→hcp phase transformation also conforms to Burgers relations but become localized due to the addition of more C atoms. Because of the different phase transformation mechanisms between the high C and low C supercells, the dislocation generation mechanism is also different.

Keywords

alloydefectsphase transformation
Type
Article
Information
Journal of Materials Research , Volume 35 , Issue 14 , 28 July 2020 , pp. 1803 - 1816
Check for updates
Copyright
Copyright © Materials Research Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Kelly, P.M.: Phase Transformations in Steels (Woodhead Publishing, Cambridge, UK, 2012).Google Scholar
Nishiyama, Z.: 5-Conditions for Martensite Formation and Stabilization of Austenite in Martensitic Transformation (Academic Press, London, UK, 1978).Google Scholar
Sauveur, A.: What is a steel another answer. Iron Age 113, 581 (1924).Google Scholar
Huang, C.X., Yang, G., Gao, Y.L., Wu, S.D., and Li, S.X.: Investigation on the nucleation mechanism of deformation-induced martensite in an austenitic stainless steel under severe plastic deformation. J. Mater. Res. 22, 724 (2011).CrossRefGoogle Scholar
Kühn, U., Romberg, J., Mattern, N., Wendrock, H., and Eckert, J.: Transformation-induced plasticity in Fe–Cr–V–C. J. Mater. Res. 25, 368 (2011).CrossRefGoogle Scholar
Bain, E.C.: The nature of martensite. Trans. AIME 79, 25 (1924).Google Scholar
Kurdjumov, G. and Sachs, G.: Über den Mechanismus der Stahlhartung. Zeitschr. Phys. 74, 325 (1930).CrossRefGoogle Scholar
Nishiyama, Z.: X-ray investigation of the mechanism of the transformation from face centered cubic lattice to body centered cubic. Sci. Rep. Tohoku Univ. 23, 637 (1934).Google Scholar
Burgers, W.G.: On the process of transition of the cubic-body-centered modification into the hexagonal-close-packed modification of zirconium. Physica 1, 561 (1934).CrossRefGoogle Scholar
Bogers, A.J. and Burgers, W.G.: Partial dislocations on the {110} planes in the B.C.C. lattice and the transition of the F.C.C. into the B.C.C. lattice. Acta Metall. 12, 255 (1964).CrossRefGoogle Scholar
Olson, G.B. and Cohen, M.: A mechanism for the strain-induced nucleation of martensitic transformations. J. Less-Common Met. 28, 107 (1972).CrossRefGoogle Scholar
Nishiyama, Z.: 6-The Crystallographic Theory of Martensitic Transformations in Martensitic Transformation (Academic Press, London, UK, 1978).Google Scholar
Bunshah, R. and Mehl, R.: Rate of propagation of martensite. Trans. AIME 197, 1251 (1953).Google Scholar
Stukowski, A.: Visualization and analysis of atomistic simulation data with OVITO: The Open Visualization Tool. Modell. Simul. Mater. Sci. Eng. 18, 2154 (2010).CrossRefGoogle Scholar
Li, J.: AtomEye: An efficient atomistic configuration viewer. Model. Simul. Mater. Sci. 11, 173 (2003).CrossRefGoogle Scholar
Bos, C., Sietsma, J., and Thijsse, B.J.: Molecular dynamics simulation of interface dynamics during the fcc-bcc transformation of a martensitic nature. Phys. Rev. B 73, 104 (2006).CrossRefGoogle Scholar
Wang, B., Sak-Saracino, E., Gunkelmann, N., and Urbassek, H.M.: Molecular-dynamics study of the α↔γ phase transition in Fe–C. Comput. Mater. Sci. 82, 399 (2014).CrossRefGoogle Scholar
Entel, P., Meyer, R., Kadau, K., Herper, H.C., and Hoffmann, E.: Martensitic transformations: First-principles calculations combined with molecular-dynamics simulations. Eur. Phys. J. B 5, 379 (1998).CrossRefGoogle Scholar
Karewar, S., Sietsma, J., and Santofimia, M.J.: Effect of pre-existing defects in the parent fcc phase on atomistic mechanisms during the martensitic transformation in pure Fe: A molecular dynamics study. Acta Mater. 142, 71 (2018).CrossRefGoogle Scholar
Nishiyama, Z.: 3-Crystallography of Martensites—Special Phenomena in Martensitic Transformation (Academic Press, London, UK, 1978).Google Scholar
Nguyen, T.Q., Sato, K., and Shibutani, Y.: Development of Fe-C interatomic potential for carbon impurities in α-iron. Comput. Mater. Sci. 150, 510 (2018).CrossRefGoogle Scholar
Wang, B., Sak-Saracino, E., Sandoval, L., and Urbassek, H.M.: Martensitic and austenitic phase transformations in Fe–C nanowires. Modell. Simul. Mater. Sci. Eng. 22, 045003 (2014).CrossRefGoogle Scholar
Karewar, S., Sietsma, J., and Santofimia, M.: Effect of C on the martensitic transformation in Fe-C alloys in the presence of pre-existing defects: A molecular dynamics study. Crystals 9, 99 (2019).CrossRefGoogle Scholar
Luu, H.-T. and Gunkelmann, N.: Pressure-induced phase transformations in Fe-C: Molecular dynamics approach. Comput. Mater. Sci. 162, 295 (2019).CrossRefGoogle Scholar
Engin, C. and Urbassek, H.M.: Molecular-dynamics investigation of the fcc→bcc phase transformation in Fe. Comput. Mater. Sci. 41, 297 (2008).CrossRefGoogle Scholar
Patterson, R.L. and Wayman, G.: The crystallography and growth of partially-twinned martensite plates in Fe-Ni alloys. Acta Metall. 14, 347 (1966).CrossRefGoogle Scholar
Shimizu, K.-i.: Direct observation of sub-structures of the martensite in Fe-Ni alloy by means of electron microscopy. J. Phys. Soc. Jpn. 17, 508 (1962).CrossRefGoogle Scholar
Patterson, R. and Wayman, C.: Internal twinning in ferrous martensites. Acta Metall. 12, 1306 (1964).CrossRefGoogle Scholar
Greninger, A.B. and Troiano, A.R.: The mechanism of Martensite formation. JOM 1, 590 (1949).CrossRefGoogle Scholar
Ou, X.: Molecular dynamics simulations of fcc-to-bcc transformation in pure iron: A review. Mater. Sci. Technol. 33, 822 (2016).CrossRefGoogle Scholar
Sun, B., Ouyang, W.Z., Ren, J.J., Mi, L.W., and Guo, W.: Fcc -> bcc -> hcp successive phase transformations in the strained ultrathin copper film: A molecular dynamic simulation study. Mater. Chem. Phys. 223, 171 (2019).CrossRefGoogle Scholar
Ölander, A.: The crystal structure of AuCd. Z. Kristallogr. Crystall. Mater. 83, 145 (1932).Google Scholar
Basinski, Z.S. and Christian, J.W.: Crystallography of deformation by twin boundary movements in indium-thallium alloys. Acta Metall. 2, 101 (1954).CrossRefGoogle Scholar
Ping, D.H., Guo, S.Q., Imura, M., Liu, X., Ohmura, T., Ohnuma, M., Lu, X., Abe, T., and Onodera, H.: Lath formation mechanisms and twinning as lath martensite substructures in an ultra low-carbon iron alloy. Sci. Rep. 8, 14264 (2018).CrossRefGoogle Scholar
Burkart, M. and Read, T.: Diffusionless phase change in the Indium-Thallium system. Trans. AIMME 197, 1516 (1953).Google Scholar
Gunkelmann, N., Ledbetter, H., and Urbassek, H.M.: Experimental and atomistic study of the elastic properties of α′ Fe–C martensite. Acta Mater. 60, 4901 (2012).CrossRefGoogle Scholar
Becquart, C.S., Raulot, J.M., Bencteux, G., Domain, C., Perez, M., Garruchet, S., and Nguyen, H.: Atomistic modeling of an Fe system with a small concentration of C. Comput. Mater. Sci. 40, 119 (2007).CrossRefGoogle Scholar
Janßen, J., Gunkelmann, N., and Urbassek, H.M.: Influence of C concentration on elastic moduli of α′-Fe1−xCx alloys. Philos. Mag. 96, 1448 (2016).CrossRefGoogle Scholar
Lee, B.-J.: A modified embedded-atom method interatomic potential for the Fe–C system. Acta Mater. 54, 701 (2006).CrossRefGoogle Scholar
Stukowski, A., Bulatov, V.V., and Arsenlis, A.: Automated identification and indexing of dislocations in crystal interfaces. Model. Simul. Mater. Sci. 20, 085007 (2012).CrossRefGoogle Scholar
Lee, B.-J. and Baskes, M.: Second nearest-neighbor modified embedded-atom-method potential. Phys. Rev. B 62, 8564 (2000).CrossRefGoogle Scholar
Lee, B.-J., Baskes, M.I., Kim, H., and Koo Cho, Y.: Second nearest-neighbor modified embedded atom method potential for BCC transition metals. Phys. Rev. B 64, 184102 (2001).CrossRefGoogle Scholar
Mohammadzadeh, M. and Mohammadzadeh, R.: Effect of interstitial and substitution alloying elements on the intrinsic stacking fault energy of nanocrystalline fcc-iron by atomistic simulation study. Appl. Phys. A 123, 720 (2017).CrossRefGoogle Scholar
Lu, S., Li, R., Kadas, K., Zhang, H., Tian, Y., Kwon, S.K., Kokko, K., Hu, Q.M., Hertzman, S., and Vitos, L.: Stacking fault energy of C-alloyed steels: The effect of magnetism. Acta Mater. 122, 72 (2017).CrossRefGoogle Scholar
Lee, T.-H., Shin, E., Oh, C.-S., Ha, H.-Y., and Kim, S.-J.: Correlation between stacking fault energy and deformation microstructure in high-interstitial-alloyed austenitic steels. Acta Mater. 58, 3173 (2010).CrossRefGoogle Scholar
Huang, T., Dan, W., and Zhang, W.: Study on the strain hardening behaviors of TWIP/TRIP steels. Metall. Mater. Trans. A 48, 4553 (2017).CrossRefGoogle Scholar
Freitas, R., Asta, M., and de Koning, M.: Nonequilibrium free-energy calculation of solids using LAMMPS. Comput. Mater. Sci. 112, 333 (2016).CrossRefGoogle Scholar
Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1 (1995).CrossRefGoogle Scholar
Stukowski, A.: Structure identification methods for atomistic simulations of crystalline materials. Modell. Simul. Mater. Sci. Eng. 20, 45021 (2012).CrossRefGoogle Scholar
Supplementary material: Image

Jiao et al. supplementary material

Jiao et al. supplementary material 1

Download Jiao et al. supplementary material(Image)
Image 3.1 MB
Supplementary material: Image

Jiao et al. supplementary material

Jiao et al. supplementary material 2

Download Jiao et al. supplementary material(Image)
Image 1.9 MB