Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Stan, Felicia
and
Fetecau, Catalin
2013.
Characterization of viscoelastic properties of molybdenum disulphide filled polyamide by indentation.
Mechanics of Time-Dependent Materials,
Vol. 17,
Issue. 2,
p.
205.
Zhang, Q.
Le Roy, R.
Vandamme, M.
and
Zuber, B.
2013.
Long-Term Creep Properties of Cementitious Materials - Comparing Compression Tests on Concrete with Microindentation Tests on Cement.
p.
1596.
Vandamme, M.
and
Ulm, F.-J.
2013.
Nanoindentation investigation of creep properties of calcium silicate hydrates.
Cement and Concrete Research,
Vol. 52,
Issue. ,
p.
38.
Vandamme, M.
Zhang, Q.
Ulm, F.-J.
Le Roy, R.
Zuber, B.
Gartner, E.
and
Termkhajornkit, P.
2013.
Creep Properties of Cementitious Materials from Indentation Testing: Significance, Influence of Relative Humidity, and Analogy Between C-S-H and Soils.
p.
48.
Sorelli, L.
Pham, D.-T.
Vallée, D.
Chen, J.
and
Fafard, M.
2013.
Finite Element Based Characterization of the Creep Properties of the Cement Paste Phases by Coupling Nanoindentation Technique and SEM-EDS.
p.
182.
Zhang, Qing
Le Roy, Robert
Vandamme, Matthieu
and
Zuber, Bruno
2014.
Long-term creep properties of cementitious materials: Comparing microindentation testing with macroscopic uniaxial compressive testing.
Cement and Concrete Research,
Vol. 58,
Issue. ,
p.
89.
Venkovic, N.
Sorelli, L.
and
Martirena, F.
2014.
Nanoindentation study of calcium silicate hydrates in concrete produced with effective microorganisms-based bioplasticizer.
Cement and Concrete Composites,
Vol. 49,
Issue. ,
p.
127.
Herbert, Erik G.
Sudharshan Phani, P.
and
Johanns, Kurt E.
2015.
Nanoindentation of viscoelastic solids: A critical assessment of experimental methods.
Current Opinion in Solid State and Materials Science,
Vol. 19,
Issue. 6,
p.
334.
Jacobo, V. H.
Ortiz, A.
and
Schouwenaars, R.
2016.
Indentation Curves in Viscoplastic Alloys: Mathematical Model, Fitting Procedures, and Application to the Room-Temperature Creep of an Al-Sn Alloy.
Advances in Materials Science and Engineering,
Vol. 2016,
Issue. ,
p.
1.
Sun, Yuhao
Aman, Michael
and
Espinoza, D. Nicolas
2016.
Assessment of mechanical rock alteration caused by CO2⿿water mixtures using indentation and scratch experiments.
International Journal of Greenhouse Gas Control,
Vol. 45,
Issue. ,
p.
9.
Photiou, D.
Prastiti, N.
Sarris, E.
and
Constantinides, G.
2016.
On the conical indentation response of elastic auxetic materials: Effects of Poisson's ratio, contact friction and cone angle.
International Journal of Solids and Structures,
Vol. 81,
Issue. ,
p.
33.
Chen, Zhao
Sorelli, Luca
Frech-Baronet, Jessy
Sanahuja, Julien
Vandamme, Matthieu
and
Chen, Jeffrey
2017.
Duality between Creep and Relaxation of a Cement Paste at Different Levels of Relative Humidity: Characterization by Microindentation and Analytical Modeling.
Journal of Nanomechanics and Micromechanics,
Vol. 7,
Issue. 4,
Wei, Ya
Liang, Siming
and
Gao, Xiang
2017.
Indentation creep of cementitious materials: Experimental investigation from nano to micro length scales.
Construction and Building Materials,
Vol. 143,
Issue. ,
p.
222.
Constantinou, M.
Pervolaraki, M.
Koutsokeras, L.
Prouskas, C.
Patsalas, P.
Kelires, P.
Giapintzakis, J.
and
Constantinides, G.
2017.
Enhancing the nanoscratch resistance of pulsed laser deposited DLC films through molybdenum-doping.
Surface and Coatings Technology,
Vol. 330,
Issue. ,
p.
185.
Constantinou, M.
Pervolaraki, M.
Nikolaou, P.
Prouskas, C.
Patsalas, P.
Kelires, P.
Giapintzakis, J.
and
Constantinides, G.
2017.
Microstructure and nanomechanical properties of pulsed excimer laser deposited DLC:Ag films: Enhanced nanotribological response.
Surface and Coatings Technology,
Vol. 309,
Issue. ,
p.
320.
Photiou, D.
Sarris, E.
and
Constantinides, G.
2017.
Erratum to “On the conical indentation response of elastic auxetic materials: Effects of Poisson's ratio, contact friction and cone angle” [Int. J. Solids Struct. 81 (2016) 33–42].
International Journal of Solids and Structures,
Vol. 110-111,
Issue. ,
p.
404.
Frech-Baronet, J.
Sorelli, L.
and
Charron, J.-P.
2017.
New evidences on the effect of the internal relative humidity on the creep and relaxation behaviour of a cement paste by micro-indentation techniques.
Cement and Concrete Research,
Vol. 91,
Issue. ,
p.
39.
Akono, Ange-Therese
and
Ulm, Franz-Josef
2017.
Microscopic Toughness of Viscous Solids via Scratching: From Amorphous Polymers to Gas Shale.
Journal of Nanomechanics and Micromechanics,
Vol. 7,
Issue. 3,
Zhang, Chi
Sorelli, Luca
Fournier, Benoît
Duchesne, Josée
Bastien, Josée
and
Chen, Zhao
2017.
Stress-relaxation of crystalline alkali-silica reaction products: Characterization by micro- and nanoindentation and simplified modeling.
Construction and Building Materials,
Vol. 148,
Issue. ,
p.
455.
Kabir, Pooyan
Ulm, Franz-Josef
and
Akono, Ange-Therese
2017.
Rate-independent fracture toughness of gray and black kerogen-rich shales.
Acta Geotechnica,
Vol. 12,
Issue. 6,
p.
1207.
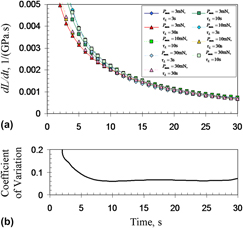
 can be measured independently of any plastic deformation exhibited during loading through
can be measured independently of any plastic deformation exhibited during loading through  , where a(t) is the contact radius, h(t) is the displacement of the contact probe, and Pmax is the constant applied load during the creep phase. These analytical relations were compared with numerical simulations of conical indentation creep for a viscoelastoplastic material and validated against sharp indentation creep experiments conducted on polystyrene. The derived relations enable extraction of viscoelastic material characteristics, even if sharp probes confer concurrent plasticity, applicable for a general axisymmetric contact probe geometry and a general time-independent plasticity.
, where a(t) is the contact radius, h(t) is the displacement of the contact probe, and Pmax is the constant applied load during the creep phase. These analytical relations were compared with numerical simulations of conical indentation creep for a viscoelastoplastic material and validated against sharp indentation creep experiments conducted on polystyrene. The derived relations enable extraction of viscoelastic material characteristics, even if sharp probes confer concurrent plasticity, applicable for a general axisymmetric contact probe geometry and a general time-independent plasticity.