Introduction
Near-α and α + β titanium alloys are used for flight-critical rotating hardware in the fan and compressor section of gas turbine engines. To develop the appropriate balance of mechanical properties, these alloys are subjected to a complex, multistep thermomechanical processing route. A typical sequence to convert an ingot to billet involves one or more homogenization steps and a series of hot working steps both above and below the β transus. An allotropic phase transformation, β → α + β, occurs each time the material is cooled from above the β transus and vice versa [Reference Semiatin, Seetharaman and Weiss1].
Because of the limited thermal conductivity of titanium and the volume of material during the large-scale intermediate stages of conversion, large colonies of aligned α platelets form in Burgers orientation relationship (BOR) with the parent β phase [Reference Burgers2]. The BOR aligns (0001)‖{110} and ![]() $\left\langle {11\bar{2}0} \right\rangle$‖〈111〉 [Reference Dahmen3]. It is desirable to refine the large colonies by α + β hot working because the lamellar microstructure resulting from the allotropic transformation has low strength, limited ductility, and poor fatigue resistance [Reference Banerjee and Williams4]. The dynamic and static processes for spheroidization of α laths have been studied extensively [Reference Weiss and Semiatin5, Reference Stefansson and Semiatin6, Reference Stefansson, Semiatin and Eylon7, Reference Poths, Wynne, Rainforth, Beynon, Angella and Semiatin8, Reference Peters, Lütjering and Ziegler9, Reference Semiatin and Furrer10]. The primary mechanism begins with dynamic formation of subgrain boundaries across the alpha laths that increase in misorientation with increasing strain [Reference Mironov, Murzinova, Zherebtsov, Salishchev and Semiatin11]. The spheroidization process proceeds statically through subsequent heat treatment, activating diffusional processes like thermal grooving to balance interfacial energies [Reference Weiss and Semiatin5, Reference Weiss, Froes, Eylon and Welsch12] and termination end migration [Reference Semiatin, Stefansson and Doherty13, Reference Park, Won, Park, Semiatin and Lee14]. By comparison, behavior of the β phase has received considerably less attention, and it is generally assumed that the β phase must also be recrystallized during the spheroidization process.
$\left\langle {11\bar{2}0} \right\rangle$‖〈111〉 [Reference Dahmen3]. It is desirable to refine the large colonies by α + β hot working because the lamellar microstructure resulting from the allotropic transformation has low strength, limited ductility, and poor fatigue resistance [Reference Banerjee and Williams4]. The dynamic and static processes for spheroidization of α laths have been studied extensively [Reference Weiss and Semiatin5, Reference Stefansson and Semiatin6, Reference Stefansson, Semiatin and Eylon7, Reference Poths, Wynne, Rainforth, Beynon, Angella and Semiatin8, Reference Peters, Lütjering and Ziegler9, Reference Semiatin and Furrer10]. The primary mechanism begins with dynamic formation of subgrain boundaries across the alpha laths that increase in misorientation with increasing strain [Reference Mironov, Murzinova, Zherebtsov, Salishchev and Semiatin11]. The spheroidization process proceeds statically through subsequent heat treatment, activating diffusional processes like thermal grooving to balance interfacial energies [Reference Weiss and Semiatin5, Reference Weiss, Froes, Eylon and Welsch12] and termination end migration [Reference Semiatin, Stefansson and Doherty13, Reference Park, Won, Park, Semiatin and Lee14]. By comparison, behavior of the β phase has received considerably less attention, and it is generally assumed that the β phase must also be recrystallized during the spheroidization process.
However, some reconstructions of transformed β packets in bimodal microstructures [Reference Banerjee and Williams4, Reference Germain, Gey, Humbert, Bocher and Jahazi15] have revealed that packets of adjacent transformed β may have low misorientation over long ranges of microstructure. To be consistent with the prevalent terminology in the titanium literature, we hereafter refer to the long–range correlation of beta phase orientations as “β microtexture.”
The origins of β microtexture can be traced back to an intermediate mill processing step in which the material is β annealed and quenched for the last time before all subsequent working is performed in the two-phase field. During this step, the prior β grain size is set and large colonies in BOR with the parent β phase are formed during cooling. During the remaining α + β hot working steps, three possibilities for microstructure evolution may be encountered:
(i) Antirotation: Burger-related colonies in unstable orientations with respect to the imposed deformation may rotate in different directions, resulting in high misorientation from the initial BOR.
(ii) Corotation: Colonies in unstable orientations may rotate cooperatively toward a stable end configuration, maintaining the BOR.
(iii) Stable Orientations: Colonies in stable orientations will not undergo significant rotation and the BOR will survive.
We hypothesize that β microtexture may persist through large strain deformation under the second condition, with corotation of both phases that maintains the BOR, and also under the third condition, with minimal rotation of both phases. Under these assumptions, there should exist some ranges of orientation space that favor the breakdown of lamellar colonies and others ranges where breakdown is not favorable. If this is the case, the colony orientations for a given loading direction that correspond to each of these conditions can be predicted through simple plastic rotation arguments. In this work, this hypothesis is tested using the viscoplastic self consistent (VPSC) polycrystal plasticity model.
Results and discussion
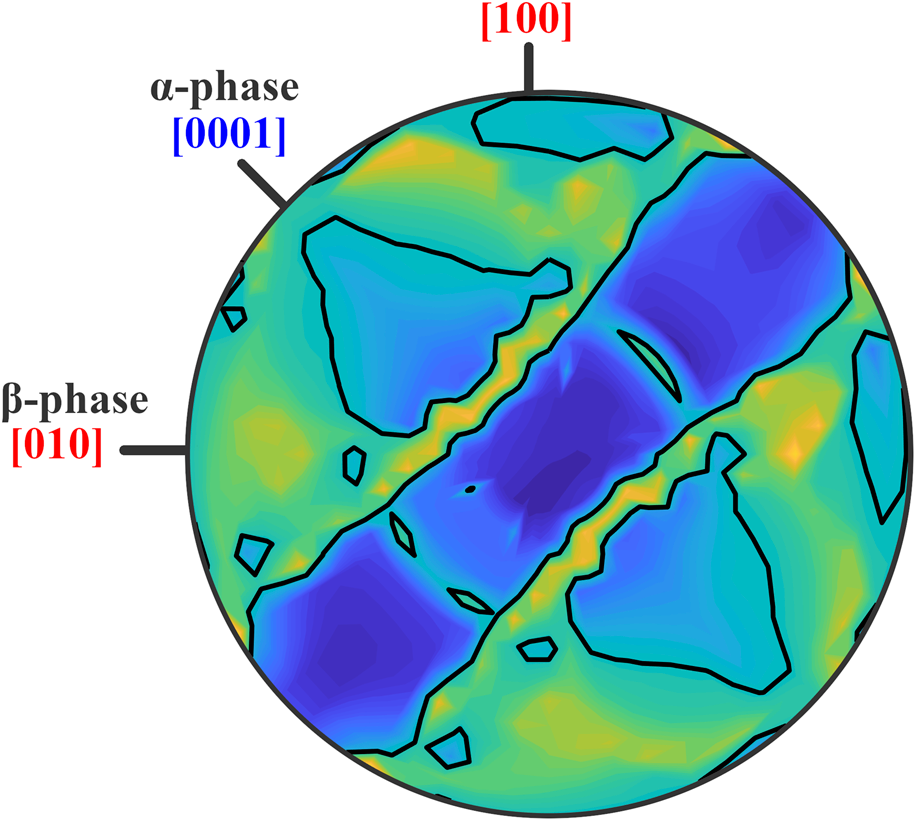
The initial colony orientation is illustrated in Fig. 1. All spherical projection plots presented as part of this work are equal angle projections plotted in reference to this initial orientation. The blue (α phase) and red (β phase) coloring is used throughout this work. More than 900 uniaxial compression directions were simulated as described in the Methods section, uniformly sampling one hemisphere of orientation space to take advantage of the loading symmetry associated with uniaxial tests. Deformation was carried out to a compressive strain of 1.0.

Figure 1: Initial α (blue) + β (red) colony orientation, plotted on an upper hemisphere equal angle projection. All of the included spherical projection plots are relative to this orientation relationship.
At each VPSC deformation step, the angular deviation from the original ideal BOR was calculated for each loading direction. Animated GIFs of the evolution of this misorientation angle over the full range of strains are presented in the Supplementary material, Fig. S1. The misorientation angles at the final strain of 1.0 are presented in Fig. 2(a). Interestingly, the VPSC results for some orientations predict that the maximum misorientation occurs at an intermediate deformation step instead of at the final strain. The maximum misorientation predicted for each loading direction is plotted in Fig. 2(b). An animated GIF showing the maximum misorientation evolving with strain is presented in the Supplementary material Fig. S2. In these plots, high misorientation angles correspond to the antirotation condition and would be predicted to result in more rapid globularization. Low misorientation angles, primarily present for loading along the 〈a〉 directions of the α phase, could correspond to either corotation or initially stable orientations.

Figure 2: Maximum misorientation from the initial BOR (a) at the final strain of 1.0 and (b) reached at any strain during deformation. A black contour line indicates a misorientation of 20° from BOR. The indicated crystallographic directions in this and future plots show the α and β phase orientations as demonstrated in Fig. 1.
The misorientation of each phase relative to its initial orientation was used to distinguish between loading directions undergoing corotation versus stable orientations. These changes in orientation of the individual α and β phases during loading is illustrated in Fig. 3 at the final strain increment. Animated GIFs of the evolution with strain are available in Supplementary material Figs. S3 and S4. For the β phase, stable orientations corresponded to loading along 〈001〉 or 〈111〉 directions. For the α phase, stable orientations were loading along the ![]() $\left\langle {11\bar{2}0} \right\rangle$ or at angles of approximately 15° from the c axis.
$\left\langle {11\bar{2}0} \right\rangle$ or at angles of approximately 15° from the c axis.

Figure 3: Misorientation of the α and β phases at a strain of 1.0 relative to their initial orientations.
The relationship between the single-phase misorientation plots and the BOR deviation plot is clear; the low misorientation “band” in Fig. 2 corresponds to the coincidence of the 〈a〉 directions in the basal plane with the β slip directions in the (110) plane.
Cross-referencing Figs. 2 and 3 allows for classification of each loading direction into the categories of corotation, antirotation, or stable orientation, as shown in Fig. 4. As a preliminary binning strategy, a threshold of 20° was used as the cutoff for “high” misorientation. The selection of an appropriate threshold is further discussed below. Using conditional comparisons of the misorientation matrices, Fig. 4 plots how regions of orientation space correspond to the three hypothesized conditions. Under this assumed threshold, corotation is relatively uncommon but does occur, whereas antirotation or stable orientations dominate. This suggests that cooperative rotation of α and β to maintain the BOR is a minor factor in the persistence of lamellar colonies through deformation processing. Instead, the grains either rotate apart or simply do not experience significant rotation during plastic deformation.

Figure 4: Binning of loading orientations into corotation (light gray), initially stable orientations (dark gray) or antirotation (red) using a threshold of 20°. White areas are indeterminate under this binning strategy.
In reality, the selection of the threshold is more qualitative than quantitative. A physically based estimate of a threshold would be 10–15°, as that is a misorientation corresponding to the formation of a “high angle grain boundary.” However, VPSC simulations are notorious for overpredicting the intensity of deformation textures even when the texture is qualitatively correct [Reference Miller, Berman, Beyerlein and Pollock16, Reference Miller, Berman, Beyerlein, Jones and Pollock17, Reference Miller, Semiatin, Szczepanski and Pilchak18, Reference Vogel, Beyerlein, Bourke, Tomé, Rangaswamy, Xu and Langdon19, Reference Vogel, Alexander, Beyerlein, Bourke, Brown, Clausen, Tomé, Von Dreele, Xu and Langdon20, Reference Carpenter, McCabe, Zheng, Wynn, Mara and Beyerlein21, Reference Li, Beyerlein, Alexander and Vogel22, Reference Li, Beyerlein, Necker, Alexander and Bourke23]. Because of this known behavior, the authors selected a higher initial threshold guess of 20°. Calibration and refinement of the thresholding conditions require comparison to experiment.
The most relevant experimental work in the literature is that of Bieler and Semiatin [Reference Bieler and Semiatin24], who used electron backscatter diffraction (EBSD) to study the effect of axisymmetric compression on globularization of Ti–6Al–4V alloy containing colonies of approximately 100 μm inside of 400 μm prior beta grains. Specifically, they considered the dependence of globularization on colony orientation. Notably, the number of studied colonies was small due to the speed limitations of EBSD at the time of the work. This produces limited fidelity in orientation space. Nonetheless, they found that the rate of globularization is inhibited when the c axis of the α phase is less than 15° or greater than 75° from the loading direction.
This condition is overlaid on the plot of deviation from initial BOR in Fig. 5, where the loading directions without an overlay were observed to have sluggish globularization kinetics. Loading directions lying near or in the basal plane show excellent agreement between the experimental observations and the VPSC simulations. This comparison suggests that the 20° threshold is appropriate, although further data collection may lead to refinement. An animated GIF showing binning as a function of the threshold is presented in the Supplementary material Fig. S5.

Figure 5: Results from Bieler and Semiatin superimposed on the results from Fig. 2. Unaltered regions were observed to have sluggish globularization kinetics.
Careful consideration is necessary when discussing grains whose c-axis is nearly parallel to the loading direction. In the VPSC simulations, these loading directions predict moderate antirotation, suggesting no issues with globularization. However, this is not what has been experimentally observed. These hard orientations often undergo kinking (buckling), leading to nonuniform globularization behavior. The buckled segments tend to rapidly globularize, while the remaining segments of hard orientation remain lamellar and resist globularization [Reference Bieler and Semiatin24]. This is in apparent contrast to the VPSC results presented herein.
However, loading aligned with the c-axis is a hard orientation; in real multicolony specimens, other colonies would preferentially deform. The effective strain in colonies of hard orientations would be lower, and buckling is not possible in the remaining short segments. If single-colony compression were carried out to large strains for hard orientations to achieve the nominal strains (without buckling), globularization would be predicted, but this is not physical for typical Ti processing. Because of these issues, VPSC simulations using stress control may have more predictive power for polycolony specimens than those using strain control. Further experimental work on hard colonies is necessary for more direct experimental comparison.
Bieler and Semiatin also drew conclusions about the contribution of slip system activity to lamellar breakdown. They attributed the enhanced rate of lamellar breakdown in the 15°–75° range around the c axis to the combination of basal and prismatic slip systems acting synergistically to facilitate globularization.
This combined slip criterion can be compared to the slip system activities predicted by the VPSC model, as illustrated in Fig. 6. As shown in subfigures, Figs. 6(a) and 6(b), loading near parallel to the c-axis does result in both low basal slip activity and low prismatic slip activity; this is strongly in agreement with Bieler and Semiatin for these orientations. The subfigure Fig. 6(c) illustrates the reliance on pyramidal 〈c + a〉 slip for these loading directions.

Figure 6: VPSC predicted (a) basal, (b) prismatic, and (c) pyramidal slip activity as a function of loading direction. Presented on a scale normalized to total slip system activity from 0 (dark) to 1 (white).
Further insight into the relationship between total slip activity and the resulting crystal rotations can be gained by looking at the axes about which rotation between the initial and final orientations is occurring, particularly within the α phase (Figs. 7 and S6). These rotation axes can be compared with the Taylor axes for different slip families. For the α phase, many rotations appear in red, corresponding to rotation around the c axis caused by primarily prismatic slip. Under these near single-slip conditions, it would be possible to undergo recovery instead of recrystallization and lamellar breakdown. Other loading directions that accumulate significant misorientation are clearly in multiple slip orientations.

Figure 7: α phase misorientation axes at a strain of 1.0 relative to the initial orientation.
Extended globularization criteria including both slip and crystal rotation are proposed. It is suggested that both antirotation of the two phases and combined activity of basal and prismatic slip are necessary for globularization. This set of combined criteria can be justified from a microstructural perspective, as discussed below.
Bieler and Semiatin state that the activity of both basal and prismatic slip is necessary to “slice” the lamella into smaller pieces via slip transmission. Slip transmission through the α–β interface has been observed for both basal and prismatic slip [Reference Echlin, Stinville, Miller, Lenthe and Pollock25]. However, the present results suggest that slip transmission is not the sole reason for the importance of combined basal and prismatic slip, because the present model would not capture transmission behavior. Additionally, if slip transmission was the defining factor, the activity of 〈a1〉 and 〈a2〉 slip would be predicted to be the most important, as these are the Burgers vectors with the lowest misalignment across the BOR interface (and therefore the most likely to undergo slip transmission). Instead, the summation of all three 〈a〉 Burgers vectors has the most predictive power.
Rather than slip transmission, the contribution of multiple basal and prismatic slip systems is likely related to recrystallization criteria which have been discussed in other hcp alloys, most notably Mg. In Mg alloys, grains where multiple Burgers vectors are active recrystallize more readily. This is because the formation of a high angle boundaries is dependent on the synergistic activity of multiple basal and prismatic slip families to rotate the subgrain away from the parent [Reference Hadorn, Hantzsche, Yi, Bohlen, Letzig, Wollmershauser and Agnew26, Reference Hadorn, Hantzsche, Yi, Bohlen, Letzig and Agnew27, Reference Miller and Pollock28].
Based on the results of this work, for lamellar α–β Ti colonies, antirotation of the two phases is necessary to promote breakdown of the BOR. Additionally, synergistic activity of basal and prismatic slip in the α phase is necessary to promote the formation of smaller equiaxed α grains and potentially to break up the β phase lamella.
In summary, the results of our VPSC model agree well with the existing empirical work studying the mechanisms of lamellar breakdown in α + β titanium alloys. Our model agrees with the experimental observation that basal and prism slip work cooperatively to facilitate globularization and provides insight into the loading orientation dependence of slip system activity. The results of this model also suggest that there is substantially more to the orientation dependence of globularization than the previously reported basal pole tilt criteria. Of particular interest would be basal pole tilts of approximately 45° where there is a range of predicted globularization behavior. This is a potential avenue for further experimental study.
Summary and conclusions
In this work, the VPSC polycrystal plasticity model was used to predict deformation behavior of α + β colonies as a function of loading direction. It was demonstrated that the colony crystal rotation behavior can be classified into “corotation” where both phases undergo similar rotations, “antirotation” in which the phases rotate apart, or minimal rotation when the initial orientation was stable for both phases. However, this alone was demonstrated to be an insufficient criterion to predict globularization. Orientations that have been reported to undergo globularization readily must both (i) undergo significant antirotation during deformation and (ii) have substantial amounts of both basal and prismatic slip.
These findings illustrate that globularization behavior in two-phase Ti alloys can be predicted with substantial accuracy using computationally inexpensive mean-field polycrystal plasticity methods. Additionally, it suggests that there is additional detail to the orientation dependence of globularization kinetics that has not previously been reported based on experimental results; however, further investigation is required.
Methods
The α–β Ti system was simulated using a VPSC model to observe the rotation and corotation of the grains. This framework considers each grain as an Eshelby inclusion in a homogeneous effective medium with the elastic properties of the aggregate polycrystal [Reference Lebensohn and Tomé29]. A macroscopic deformation is imposed, and shear rates are calculated on the relevant slip systems for each grain. These shear rates are used to calculate crystallographic texture evolution, grain-scale hardening, slip activity, and macroscopic stress–strain behavior. All simulated mechanical tests in this work are uniaxial compression tests along a specified direction relative to the colony orientation at a strain rate of 10−2 s−1. Results were not found to be strongly sensitive to the deformation rate.
The VPSC model typically uses an extended Voce law to describe the hardening behavior of each slip system. The necessary parameters to model this behavior accurately for α + β alloys are absent in the existing literature, so in this case each system is assumed to be perfectly plastic. The τ0 (effective CRSS) values determined experimentally by Salem and Semiatin, given in Table I, were assigned in the model [Reference Salem and Semiatin30].
TABLE I: Effective critical resolved shear stress values for each slip system in a single α–β Ti colony, from Ref. Reference Salem and Semiatin30.

Nine hundred fifteen axisymmetric uniaxial compression directions were simulated, uniformly sampling one hemisphere of orientation space to eliminate redundancy from the loading symmetry associated with uniaxial tests. The BOR has monoclinic crystal symmetry [Reference Kim and Rokhlin31], which is reflected in the results presented above. Small deviations from perfect monoclinic symmetry result from rounding errors. For numerical stability, 200 identically oriented grains of each phase were simulated; the VPSC results are deterministic, so this results in only a single α and β orientation for each loading condition. Equal angle projections are used in this work to plot rotation and misorientation results in orientation space. The β phase was chosen as the origin orientation, rotating through the BOR Euler angles to establish the initial alpha orientation [Reference Dahmen3]. These figures are therefore relative to the 〈001〉 axis of the cubic β phase. Angular deviation from the initial orientation relationship is used to represent misorientations.
Deformation was simulated to a compressive strain of 1.0, with the texture being updated at strain increments of 0.05. The MTEX toolbox [Reference Bachmann, Hielscher and Schaeben32] was used to import the starting and as-deformed orientations, along with slip system activities, for further analysis. Strain evolution of misorientation and slip activity were captured by generating multiframe image files, accessible through online Supplemental material.
The code used to analyze the simulation data has been published at https://github.com/tori-miller/Ti64-VPSC-CoRotation-Analysis.
Supplementary material
To view supplementary material for this article, please visit https://doi.org/10.1557/jmr.2020.54.