Article contents
The local stress state of a running shear band in amorphous solids
Published online by Cambridge University Press: 27 May 2015
Abstract
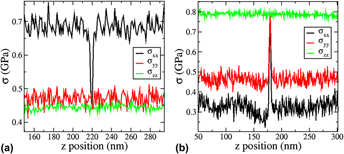
In molecular dynamics simulations, the local stress state in the shear band is examined in six different model metallic glasses and one amorphous Si system (also has been perceived as a metallic glass analog) under different loading conditions. For all but the FeP and the amorphous Si systems, the running shear band (RSB) exhibits a liquid-like hydrostatic plus shear stress state. Our results suggest that the liquid feature of a RSB is not due to temperature rise or plastic confinement but due to the disorder driven by flow, which can be offset by strong directionality in bonding, phase segregation, or aging. The knowledge of the liquid-like stress state can be conveniently utilized in experiments to infer the local stress state of the RSB from the global tensile stress for metallic glasses.
- Type
- Articles
- Information
- Copyright
- Copyright © Materials Research Society 2015
References
REFERENCES
- 6
- Cited by


