Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T12:13:12.865Z Has data issue: false hasContentIssue false
  • English
  • Français

The inverse parameter identification of Hill’48 yield function for small-sized tube combining response surface methodology and three-point bending

Published online by Cambridge University Press:  21 March 2017

Honglie Zhang  and
Yuli Liu
Honglie Zhang
Affiliation:
State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, People’s Republic of China
Yuli Liu*
Affiliation:
State Key Laboratory of Solidification Processing, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, People’s Republic of China
*
a) Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

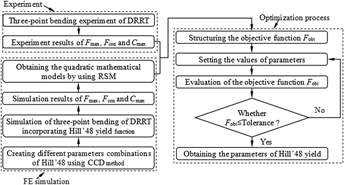
Hill’48 yield function has been widely used to describe the anisotropic behaviors of material in FE simulation of tube and sheet metal forming process. To obtain the material behaviors of small-sized H96 brass extrusion double-ridged rectangular tube (DRRT) in bending process, an inverse method combining response surface method and three-point bending was proposed to identify the parameters of Hill’48 yield function. It was found that comparing with Hill’48 yield function only considering the normal anisotropy and Mises yield function, Hill’48 yield function with the identified parameters performs the best in reproducing the material behavior of H96 brass DRRT in three-point bending process. And then Hill’48 yield function with the identified parameters was also adopted in the FE simulations of rotary draw bending of DRRT. It was observed that the prediction accuracy of cross sectional deformation of DRRT in rotary bending process was improved effectively by using Hill’48 yield function with the identified parameters. This proves that the proposed inverse method is suitable to the real forming process.

Keywords

inverse parameter identificationfinite element methodthree-point bendingHill’48 yield functionresponse surface methodsmall-sized tube
Type
Articles
Information
Journal of Materials Research , Volume 32 , Issue 12 , 28 June 2017 , pp. 2343 - 2351
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Jürgen Eckert

References

REFERENCES

Hopperstad, O.S., Berstad, T., Ilstad, H., Lademo, O.G., and Langseth, M.: Effects of the yield criterion on local deformations in numerical simulation of profile forming. J. Mater. Process. Technol. 80–81, 551–555 (1998).Google Scholar
Zhan, M., Huang, T., and Yang, H.: Variation of contractile strain ratio of Ti–3Al–2.5V tubes and its effects in tubes numerical control bending process. J. Mater. Process. Technol. 217, 165–183 (2014).Google Scholar
Cooreman, S., Lecompte, D., Sol, H., Vantomme, J., and Debruyne, D.: Identification of mechanical material behavior through inverse modeling and DIC. Exp. Mech. 48, 421–433 (2008).Google Scholar
Güner, A., Soyarslan, C., Brosius, A., and Tekkaya, A.E.: Characterization of anisotropy of sheet metals employing inhomogeneous strain fields for Yld2000-2D yield function. Int. J. Solids Struct. 49, 3517–3527 (2012).Google Scholar
Tardif, N. and Kyriakides, S.: Determination of anisotropy and material hardening for aluminum sheet metal. Int. J. Solids Struct. 49, 3496–3506 (2012).Google Scholar
Cooreman, S., Lecompte, D., Sol, H., Vantomme, J., and Debruyne, D.: Elasto-plastic material parameter identification by inverse methods: Calculation of the sensitivity matrix. Int. J. Solids Struct. 44, 4329–4341 (2007).CrossRefGoogle Scholar
Ghouati, O. and Gelin, J.C.: Identification of material parameters directly from metal forming processes. J. Mater. Process. Technol. 80–81, 560–564 (1998).Google Scholar
Chamekh, A., Salah, H.B.H., and Hambli, R.: Inverse technique identification of material parameters using finite element and neural network computation. Int. J. Adv. Manuf. Technol. 44, 173–179 (2009).Google Scholar
Malakizadi, A., Cedergren, S., Sadik, I., and Nyborg, L.: Inverse identification of flow stress in metal cutting process using response surface methodology. Simul. Model. Pract. Th. 60, 40–53 (2016).Google Scholar
Huber, E. and Tyulyukovskiyand, N.: Identification of viscoplastic material parameters from spherical indentation data: Part I. Neural networks. J. Mater. Res. 21, 664–676 (2006).Google Scholar
Malakizadi, A., Sadik, I., and Nyborg, L.: Wear mechanism of CBN inserts during machining of bimetal aluminum-grey cast iron engine block. Procedia CIRP 8, 188–193 (2013).Google Scholar
Hill, R.: A theory of the yielding and plastic flow of anisotropic metals. Proc. R. Soc. London 193, 281–297 (1948).Google Scholar
Yan, Y., Wang, H., and Li, Q.: The inverse parameter identification of Hill 48 yield criterion and its verification in press bending and roll forming process simulations. J. Manuf. Processes 20, 46–53 (2015).CrossRefGoogle Scholar
Bäker, M. and Shrot, A.: Inverse parameter identification with finite element simulations using knowledge-based descriptors. Comput. Mater. Sci. 69, 128–136 (2013).Google Scholar
Cao, J. and Lin, J.: A study on formulation of objective functions for determining material models. Int. J. Mech. Sci. 50, 193–204 (2008).CrossRefGoogle Scholar