Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-22T21:47:41.132Z Has data issue: false hasContentIssue false
  • English
  • Français

Exploring the electronic, mechanical, and anisotropy properties of novel tetragonal B2CO phase

Published online by Cambridge University Press:  20 September 2019

Mingwei Chen ,
Chao Liu ,
Meiling Liu ,
Uppalapati Pramod Kumar ,
Zihe Li ,
Lingyu Liu ,
Julong He  and
Tongxiang Liang
Mingwei Chen
Affiliation:
School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
Chao Liu*
Affiliation:
School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China; and State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China
Meiling Liu
Affiliation:
School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
Uppalapati Pramod Kumar
Affiliation:
School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
Zihe Li
Affiliation:
State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China
Lingyu Liu
Affiliation:
School of Physics and Optoelectronic Engineering, Guangdong University of Technology, Guangzhou 51006, China
Julong He
Affiliation:
State Key Laboratory of Metastable Materials Science and Technology, Yanshan University, Qinhuangdao 066004, China
Tongxiang Liang*
Affiliation:
School of Materials Science and Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, China
*
a)Address all correspondence to these authors. e-mail: [email protected]
b)e-mail: [email protected]
Get access

Abstract

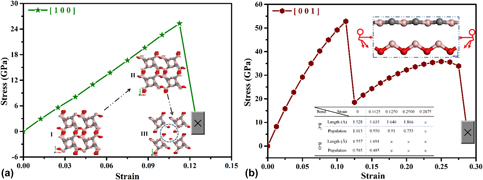
A novel tetragonal B2CO structure (tP16-B2CO), formed by strong covalent sp2–sp3 B–C and B–O bonds, was predicted with aid of an unbiased structure searching method. With the energy lower than those of previously proposed candidates, except oI16-B2CO, tP16-B2CO was identified as the thermodynamic metastable phase for B2CO compound. The elastic matrix and phonon dispersion spectra declare that tP16-B2CO is mechanically and dynamically stable. The electronic band structure calculation at ambient pressure and a series of high pressure has manifested the indirect semiconducting and band gap increases first and then decreases with pressure increases. The calculation of mechanical properties such as hardness and stress–strain relations of tP16 structure revealed its common hard nature with high hardness of 23.19 GPa and anisotropy with the max stress along [001] is far higher than that along [100].

Keywords

hardnessstress/strain relationshipstructural
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 21 , 14 November 2019 , pp. 3617 - 3626
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Tian, Y., Xu, B., and Zhao, Z.: Microscopic theory of hardness and design of novel superhard crystals. Int. J. Refract. Met. Hard Mater. 33, 93 (2012).CrossRefGoogle Scholar
Garvie, L.A.J., Hubert, H., Petuskey, W.T., McMillan, P.F., and Buseck, P.R.: High-pressure, high-temperature syntheses in the B–C–N–O system. J. Solid State Chem. 133, 365 (1997).CrossRefGoogle Scholar
Hubert, H., Garvie, L.A., Devouard, B., and McMillan, P.F.: High-pressure, high-temperature syntheses of super-hard α-Rhombohedral boron-rich solids in the BCNO. MRS Proc., 315 (Cambridge, UK, 1997).CrossRefGoogle Scholar
Bolotina, N., Dyuzheva, T., and Bendeliani, N.: Atomic structure of boron suboxycarbide B(C,O)0.155. Crystallogr. Rep. 46, 734 (2001).CrossRefGoogle Scholar
Li, Q., Chen, W.J., Xia, Y., Liu, Y.H., Wang, H.B., Wang, H., and Ma, Y.M.: Superhard phases of B2O: An isoelectronic compound of diamond. Diamond Relat. Mater. 20, 501 (2011).CrossRefGoogle Scholar
Li, Y., Li, Q., and Ma, Y.: B2CO: A potential superhard material in the B–C–O system. Europhys. Lett. 95, 66006 (2011).CrossRefGoogle Scholar
Qiao, L., Jin, Z., Yan, G., Li, P., Hang, L., and Li, L.: Density-functional-studying of oP8-, tI16-, and tP4-B2CO physical properties under pressure. J. Solid State Chem. 270, 642 (2019).CrossRefGoogle Scholar
Liu, C., Zhao, Z., Luo, K., Hu, M., Ma, M., and He, J.: Superhard orthorhombic phase of B2CO compound. Diamond Relat. Mater. 73, 87 (2017).CrossRefGoogle Scholar
Zhang, M., Yan, H., Zheng, B., and Wei, Q.: Influences of carbon concentration on crystal structures and ideal strengths of B2CXO compounds in the B–C–O system. Sci. Rep. 5, 15481 (2015).CrossRefGoogle ScholarPubMed
Liu, C., Chen, M., He, J., Yu, S., and Liang, T.: Superhard B2CO phases derived from carbon allotropes. RSC Adv. 7, 52192 (2017).CrossRefGoogle Scholar
Yan, H., Zhang, M., Wei, Q., and Zhang, Y.: A new orthorhombic ground-state phase and mechanical strengths of ternary B2CO compound. Chem. Phys. Lett. 701, 86 (2018).CrossRefGoogle Scholar
Wang, S., Oganov, A.R., Qian, G., Zhu, Q., Dong, H., Dong, X., and Davari Esfahani, M.M.: Novel superhard B–C–O phases predicted from first principles. Phys. Chem. Chem. Phys. 18, 1859 (2016).CrossRefGoogle ScholarPubMed
Qiao, L. and Jin, Z.: Two B–C–O compounds: Structural, mechanical anisotropy and electronic properties under pressure. Materials 10, 1413 (2017).CrossRefGoogle ScholarPubMed
Zhou, S. and Zhao, J.: Two-dimensional B–C–O alloys: A promising class of 2D materials for electronic devices. Nanoscale 8, 8910 (2016).CrossRefGoogle Scholar
Liu, C., Chen, M., Yang, Y., Li, J., Shao, C., Li, P., Liu, L., He, J., and Liang, T.: Theoretical exploring the mechanical and electrical properties of tI12-B6C4O2. Comput. Mater. Sci. 150, 259 (2018).CrossRefGoogle Scholar
Nuruzzaman, M., Alam, M.A., Shah, M.A.H., Parvin, F., and Zilani, M.A.K.: Investigation of thermodynamic stability, mechanical and electronic properties of superhard tetragonal B4CO4 compound: Ab initio calculations. Comput. Condens. Matter 12, 1 (2017).CrossRefGoogle Scholar
Zheng, B., Zhang, M., and Wang, C.: Exploring the mechanical anisotropy and ideal strengths of tetragonal B4CO4. Materials 10, 128 (2017).CrossRefGoogle Scholar
Mouhat, F. and Coudert, F.: Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B 90, 224104 (2014).CrossRefGoogle Scholar
Garza, A.J. and Scuseria, G.E.: Predicting band gaps with hybrid density functionals. J. Phys. Chem. Lett. 7, 4165 (2016).CrossRefGoogle ScholarPubMed
Krukau, A.V., Vydrov, O.A., Izmaylov, A.F., and Scuseria, G.E.: Influence of the exchange screening parameter on the performance of screened hybrid functionals. J. Chem. Phys. 125, 224106 (2006).CrossRefGoogle ScholarPubMed
Dias, R.P. and Silvera, I.F.: Observation of the Wigner–Huntington transition to metallic hydrogen. Science 355, 715 (2017).CrossRefGoogle ScholarPubMed
Ma, Y., Eremets, M., Oganov, A.R., Xie, Y., Trojan, I., Medvedev, S., Lyakhov, A.O., Valle, M., and Prakapenka, V.: Transparent dense sodium. Nature 458, 182 (2009).CrossRefGoogle ScholarPubMed
Wu, Z., Zhao, E., Xiang, H., Hao, X., Liu, X., and Meng, J.: Crystal structures and elastic properties of superhard IrN2 and IrN3 from first principles. Phys. Rev. B 76, 054115 (2007).CrossRefGoogle Scholar
Korozlu, N., Colakoglu, K., Deligoz, E., and Aydin, S.: The elastic and mechanical properties of MB12 (M = Zr, Hf, Y, Lu) as a function of pressure. J. Alloys Compd. 546, 157 (2013).CrossRefGoogle Scholar
Ranganathan, S.I. and Ostoja-Starzewski, M.: Universal elastic anisotropy index. Phys. Rev. Lett. 101, 055504 (2008).CrossRefGoogle ScholarPubMed
Ainsworth, R.I., Tommaso, D.D., and de Leeuw, N.H.: A density functional theory study of structural, mechanical and electronic properties of crystalline phosphorus pentoxide. J. Chem. Phys. 135, 234513 (2011).CrossRefGoogle ScholarPubMed
Bohinc, R., Žitnik, M., Bučar, K., Kavčič, M., Carniato, S., Journel, L., Guillemin, R., Marchenko, T., Kawerk, E., Simon, M., and Cao, W.: Structural and dynamical properties of chlorinated hydrocarbons studied with resonant inelastic X-ray scattering. J. Chem. Phys. 144, 134309 (2016).CrossRefGoogle ScholarPubMed
Needs, R.J. and Pickard, C.J.: Perspective: Role of structure prediction in materials discovery and design. APL Mater. 4, 053210 (2016).CrossRefGoogle Scholar
Lyakhov, A.O., Oganov, A.R., Stokes, H.T., and Zhu, Q.: New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172 (2013).CrossRefGoogle Scholar
Clark, S.J., Segall, M.D., Pickard, C.J., Hasnip, P.J., Probert, M.J., Refson, K., and Payne, M.C.: First principles methods using CASTEP. Z. Kristallogr. 220, 567 (2005).Google Scholar
Perdew, J.P., Burke, K., and Ernzerhof, M.: Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).CrossRefGoogle ScholarPubMed
Vanderbilt, D.: Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 41, 7892 (1990).CrossRefGoogle Scholar
Monkhorst, H.J. and Pack, J.D.: Special points for Brillouin-zone integrations. Phys. Rev. B 13, 5188 (1976).CrossRefGoogle Scholar
Montanari, B. and Harrison, N.: Lattice dynamics of TiO2 rutile: Influence of gradient corrections in density functional calculations. Chem. Phys. Lett. 364, 528 (2002).CrossRefGoogle Scholar
Setyawan, W. and Curtarolo, S.: High-throughput electronic band structure calculations: Challenges and tools. Comput. Mater. Sci. 49, 299 (2010).CrossRefGoogle Scholar
Lin, J., Qteish, A., Payne, M., and Heine, V.: Optimized and transferable nonlocal separable ab initio pseudopotentials. Phys. Rev. B 47, 4174 (1993).CrossRefGoogle ScholarPubMed