Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-24T16:21:11.806Z Has data issue: false hasContentIssue false
  • English
  • Français

Engineering materials properties in codimension > 0

Published online by Cambridge University Press:  26 October 2011

Paulo S. Branicio ,
Mark H. Jhon  and
David J. Srolovitz
Paulo S. Branicio
Affiliation:
Institute of High Performance Computing, Singapore 138632, Singapore
Mark H. Jhon
Affiliation:
Institute of High Performance Computing, Singapore 138632, Singapore
David J. Srolovitz*
Affiliation:
Institute of High Performance Computing, Singapore 138632, Singapore
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

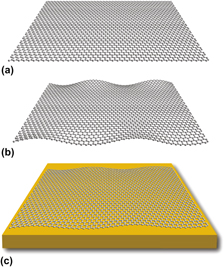
When thin nanomaterials spontaneously deform into nonflat geometries (e.g., nanorods into nanohelices, thin sheets into ruffled forms), their properties may change by orders of magnitude. We discuss this phenomenon in terms of a formal mathematical concept: codimension c = D − d, the difference between the dimensionality of space D, and that of the object d. We use several independent examples such as the edge stress of graphene nanoribbons, the elastic moduli of nanowires, and the thermal expansion of a modified bead-chain model to demonstrate how this framework can be used to generically understand some nanomaterial properties and how these properties can be engineered by using mechanical constraints to manipulate the codimension of the corresponding structure.

Keywords

Cnanostructurenanoscale
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 3: Focus Issue: Advances in Mechanics of One-Dimensional Micro/Nanomaterials , 14 February 2012 , pp. 619 - 626
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Iijima, S.: Helical microtubules of graphitic carbon. Nature 354, 56 (1991).Google Scholar
2.Dai, H.: Carbon nanotubes: Synthesis, integration, and properties. Acc. Chem. Res. 35, 1035 (2002).CrossRefGoogle ScholarPubMed
3.Duan, X. and Lieber, C.M.: General synthesis of compound semiconductor nanowires. Adv. Mater. 12, 298 (2000).3.0.CO;2-Y>CrossRefGoogle Scholar
4.Wu, Y., Xiang, J., Yang, C., Lu, W., and Lieber, C.M.: Single-crystal metallic nanowires and metal/semiconductor nanowire heterostructures. Nature 430, 61 (2004).CrossRefGoogle ScholarPubMed
5.Geim, A.K. and Novoselov, K.S.: The rise of graphene. Nat. Mater. 6, 183–191 (2007).CrossRefGoogle ScholarPubMed
6.Kong, X.Y. and Wang, Z.L.: Spontaneous polarization-induced nanohelixes, nanosprings, and nanorings of piezoelectric nanobelts. Nano Lett. 3, 1625–1631 (2003).Google Scholar
7.Pan, Z.W., Dai, Z.R., and Wang, Z.L.: Nanobelts of semiconducting oxides. Science 291, 1947–1949 (2001).CrossRefGoogle ScholarPubMed
8.Bets, K.V. and Yakobson, B.I.: Spontaneous twist and intrinsic instabilities of pristine graphene nanoribbons. Nano Res. 2, 161–166 (2009).CrossRefGoogle Scholar
9.Garcia-Ruiz, J.M., Melero-Garcia, E., and Hyde, S.T.: Morphogenesis of self-assembled nanocrystalline materials of barium carbonate and silica. Science 323, 362–365 (2009).Google Scholar
10.Huang, M.H., Boone, C., Roberts, M., Savage, D.E., Lagally, M.G., Shaji, N., Qin, H., Blick, R., Nairn, J.A., and Liu, F.: Nanomechanical architecture of strained bilayer thin films: From design principles to experimental fabrication. Adv. Mater. 17, 2860–2864 (2005).CrossRefGoogle Scholar
11.Zhang, L., Deckhardt, E., Weber, A., Schonenberger, C., and Grutzmacher, D.: Controllable fabrication of SiGe/Si and SiGe/Si/Cr helical nanobelts. Nanotechnology 16, 655–663 (2005).CrossRefGoogle Scholar
12.Hazewinkel, M., Ed.: Encyclopaedia of Mathematics; Springer: New York; 1995.Google Scholar
13.Encyclopaedia of mathematics:http://eom.springer.de/C/c022870.htm (accessed August 11, 2011).Google Scholar
14.LeSar, R., Najafabadi, R., and Srolovitz, D.J.: Thermodynamics of solid and liquid embedded-atom-method metals: A variational study. J. Chem. Phys. 94, 5090–5097 (1991).CrossRefGoogle Scholar
15.Mansoori, G.A. and Canfield, F.B.: Variational approach to melting. II. J. Chem. Phys. 51, 4967–4972 (1969).CrossRefGoogle Scholar
16.Steinmetz, J., Kwon, S., Lee, H.J., Abou-Hamad, E., Almairac, R., Goze-Bac, C., Kim, H., and Park, Y.W.: Polymerization of conducting polymers inside carbon nanotubes. Chem. Phys. Lett. 431, 139–144 (2006).CrossRefGoogle Scholar
17.Steinmetz, J., Lee, H.J., Kwon, S., Lee, D.S., Goze-Bac, C., Abou-Hamad, E., Kim, H., and Park, Y.W.: Routes to the synthesis of carbon nanotube–polyacetylene composites by Ziegler–Natta polymerization of acetylene inside carbon nanotubes. Curr. Appl. Phys. 7, 39–41 (2007).CrossRefGoogle Scholar
18.Nishide, D., Wakabayashi, T., Sugai, T., Kitaura, R., Kataura, H., Achiba, Y., and Shinohara, H.: Raman spectroscopy of size-selected linear polyyne molecules C2NH2 (n = 46) encapsulated in single-wall carbon nanotubes. J. Phys. Chem. C 111, 5178–5183 (2007).CrossRefGoogle Scholar
19.Bazilevsky, A.V., Sun, K., Yarin, A.L., and Megaridis, C.M.: Selective intercalation of polymers in carbon nanotubes. Langmuir 23, 7451–7455 (2007).CrossRefGoogle ScholarPubMed
20.McIntosh, G.C., Tománek, D., and Park, Y.W.: Energetics and electronic structure of a polyacetylene chain contained in a carbon nanotube. Phys. Rev. B 67, 125419 (2003).CrossRefGoogle Scholar
21.Bao, W., Miao, F., Chen, Z., Zhang, H., Jang, W., Dames, C., and Lau, C.N.: Controlled ripple texturing of suspended graphene and ultrathin graphite membranes. Nat. Nanotechnol. 4, 562–566 (2009).CrossRefGoogle ScholarPubMed
22.Jiang, J.W., Wang, J.S., and Li, B.W.: Thermal expansion in single-walled carbon nanotubes and graphene: Nonequilibrium Green’s function approach. Phys. Rev. B 80, 205429 (2009).CrossRefGoogle Scholar
23.Zhang, D.Q., Alkhateeb, A., Han, H.M., Mahmood, H., McIlroy, D.N., and Norton, M.G.: Silicon carbide nanosprings. Nano Lett. 3, 983–987 (2003).CrossRefGoogle Scholar
24.Wahl, A.M.: Helical compression and tension springs. J. Appl. Mech. 2, A38 (1935).CrossRefGoogle Scholar
25.Ancker, C.J. Jr. and Goodier, J.N.: Pitch and curvature correction for helical springs. J. Appl. Mech. 25, 466 (1958).CrossRefGoogle Scholar
26.Young, W. and Budynas, R.: Roark’s Formulas for Stress & Strain, 7th ed.; McGraw–Hill Professional: New York; 1984.Google Scholar
27.Gass, M.H., Bangert, U., Bleloch, A.L., Wang, P., Nair, R.R., and Geim, A.K.: Free-standing graphene at atomic resolution. Nat. Nanotechnol. 3, 676–681 (2008).CrossRefGoogle ScholarPubMed
28.Tapaszto, L., Dobrik, G., Lambin, P., and Biro, L.P.: Tailoring the atomic structure of graphene nanoribbons by scanning tunnelling microscope lithography. Nat. Nanotechnol. 3, 397–401 (2008).CrossRefGoogle ScholarPubMed
29.Geim, A.K.: Graphene: Status and prospects. Science 324, 1530–1534 (2009).CrossRefGoogle Scholar
30.Jun, S.: Density-functional study of edge stress in graphene. Phys. Rev. B 78, 073405 (2008).CrossRefGoogle Scholar
31.Huang, B., Liu, M., Su, N.H., Wu, J., Duan, W.H., Gu, B.L., and Liu, F.: Quantum manifestations of graphene edge stress and edge instability: A first-principles study. Phys. Rev. Lett. 102, 166404 (2009).Google Scholar
32.Gan, C.K. and Srolovitz, D.J.: Trends in graphene edge properties and flake shapes: A first-principles study. Phys. Rev. B 81, 125445 (2010).CrossRefGoogle Scholar
33.Shenoy, V.B., Reddy, C.D., Ramasubramaniam, A., and Zhang, Y.W.: Edge-stress-induced warping of graphene sheets and nanoribbons. Phys. Rev. Lett. 101, 245501 (2008).Google Scholar
34.Rammerstorfer, F.G., Fischer, F.D., and Friedl, N.: Buckling of free infinite strips under residual stresses and global tension. J. Appl. Mech. 68, 399–404 (2001).CrossRefGoogle Scholar
35.Chen, Z.G., Zou, J., Liu, G., Li, F., Wang, Y., Wang, L., Yuan, X.L., Sekiguchi, T., Cheng, H.M., and Lu, G.Q.: Novel boron nitride hollow nanoribbons. ACS Nano 2, 2183–2191 (2008).Google Scholar
36.Campos-Delgado, J., Romo-Herrera, J.M., Jia, X., Cullen, D.A., Muramatsu, H., Kim, Y.A., Hayashi, T., Ren, Z., Smith, D.J., Okuno, Y., Ohba, T., Kanoh, H., Kaneko, K., Endo, M., Terrones, H., Dresselhaus, M.S., and Terrones, M.: Bulk production of a new form of sp2 carbon: Crystalline graphene nanoribbons. Nano Lett. 8, 2773–2778 (2008).CrossRefGoogle ScholarPubMed
37.Branicio, P.S., Gan, C.K., Jhon, M.H., and Srolovitz, D.J.: Properties on the edge: Graphene edge energies, edge stresses, edge warping, and the wulf shape of graphene flakes. Model. Simul. Mater. Sci. Eng. 19, 054002 (2011).CrossRefGoogle Scholar
38.Brenner, D.W., Shenderova, O.A., Harrison, J.A., Stuart, S.J., Ni, B., and Sinnott, S.B.: A second-generation reactive empirical bond order (REBO) potential energy expression for hydrocarbons. J. Phys.: Condens. Matter 14, 783–802 (2002).Google Scholar
39.Liu, Y., Dobrinsky, A., and Yakobson, B.I.: Graphene edge from armchair to zigzag: The origins of nanotube chirality? Phys. Rev. Lett. 105, 235502 (2010).CrossRefGoogle ScholarPubMed
40.Lu, Q. and Huang, R.: Excess energy and deformation along free edges of graphene nanoribbons. Phys. Rev. B 81, 155410 (2010).CrossRefGoogle Scholar
41.Lui, G.H., Liu, L., Mak, K.F., Flynn, G.W., and Heinz, T.F.: Ultraflat graphene. Nature 462, 339–341 (2009).Google Scholar
42.Nye, J.F.: Physical Properties of Crystals: Their Representation by Tensors and Matrices; Oxford University Press: Oxford, UK; 1984.Google Scholar
43.Ovid’ko, I.A.: Nanodefects in nanostructures. Phil. Mag. Lett. 83, 611–620 (2003).CrossRefGoogle Scholar
44.Terrones, M., Banhart, F., Grobert, N., Charlier, J.-C., Terrones, H., and Ajayan, P.M.: Molecular junctions by joining single-walled carbon nanotubes. Phys. Rev. Lett. 89, 075505 (2002).CrossRefGoogle ScholarPubMed
45.Gutkin, M.Y. and Ovid’ko, I.A.: Glide of hollow fibers at the bridging stage of fracture in ceramic nanocomposites. Scripta Mater. 59, 414–417 (2008).CrossRefGoogle Scholar
46.Gutkin, M.Y. and Ovid’ko, I.A.: Effect of y-junction nanotubes on strengthening of nanocomposites. Scripta Mater. 61, 1149–1152 (2009).CrossRefGoogle Scholar
47.Shtukenberg, A.G., Freudenthal, J., and Kahr, B.: Reversible twisting during helical hippuric acid crystal growth. J. Am. Chem. Soc. 132, 9341–9349 (2010).CrossRefGoogle ScholarPubMed
48.Liang, H. and Mahadevan, L.: The shape of a long leaf. Proc. Natl. Acad. Sci. 106, 22049–22054 (2009).CrossRefGoogle ScholarPubMed
49.Liu, D.C. and Nocedal, J.: On the limited memory BFGS method for large-scale optimization. Math. Program. 45, 503–528 (1989).CrossRefGoogle Scholar