Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Huang, Danhong
Iurov, Andrii
Gao, Fei
Gumbs, Godfrey
Cardimona, David
LeVan, Paul D.
Wijewarnasuriya, Priyalal
and
D'Souza, Arvind I.
2018.
Microscopic theory for point-defect effects on photon absorption in quantum-well systems.
p.
2.
Brudnyi, V N
Boiko, V M
Kolin, N G
Kosobutsky, A V
Korulin, A V
Brudnyi, P A
and
Ermakov, V S
2018.
Neutron irradiation-induced modification of electrical and structural properties of GaN epifilms grown on Al2O3 (0001) substrate.
Semiconductor Science and Technology,
Vol. 33,
Issue. 9,
p.
095011.
Huang, Danhong
Iurov, Andrii
Gao, Fei
Gumbs, Godfrey
and
Cardimona, D. A.
2018.
Many-Body Theory of Proton-Generated Point Defects for Losses of Electron Energy and Photons in Quantum Wells.
Physical Review Applied,
Vol. 9,
Issue. 2,
Gao, Fei
Chen, Nanjun
Huang, Danhong
Heller, Eric R.
LeVan, Paul D.
LeVan, Paul D.
Wijewarnasuriya, Priyalal
and
D'Souza, Arvind I.
2018.
Atomic-level based non-ionizing energy loss: an application to GaAs and GaN semiconductor materials.
p.
3.
Chen, Nanjun
Rasch, Erich
Huang, Danhong
Heller, Eric R.
and
Gao, Fei
2018.
Atomic-Scale Simulation for Pseudometallic Defect-Generation Kinetics and Effective NIEL in GaN.
IEEE Transactions on Nuclear Science,
Vol. 65,
Issue. 5,
p.
1108.
Pellegrino, C.
Gagliardi, A.
and
Zimmermann, C. G.
2020.
Defect spectroscopy and non-ionizing energy loss analysis of proton and electron irradiated p-type GaAs solar cells.
Journal of Applied Physics,
Vol. 128,
Issue. 19,
He, Huan
He, Chaohui
Zhang, Jiahui
Liao, Wenlong
Zang, Hang
Li, Yonghong
and
Liu, Wenbo
2020.
Primary damage of 10 keV Ga PKA in bulk GaN material under different temperatures.
Nuclear Engineering and Technology,
Vol. 52,
Issue. 7,
p.
1537.
Zutter, Brian T.
Kim, Hyunseok
Hubbard, William A.
Ren, Dingkun
Mecklenburg, Matthew
Huffaker, Diana
and
Regan, B.C.
2021.
Mapping Charge Recombination and the Effect of Point-Defect Insertion in
GaAs
Nanowire Heterojunctions.
Physical Review Applied,
Vol. 16,
Issue. 4,
Chen, Nanjun
Huang, Danhong
Heller, Eric R.
Cardimona, David A.
and
Gao, Fei
2021.
Atomistic simulation of displacement damage and effective nonionizing energy loss in InAs.
Physical Review Materials,
Vol. 5,
Issue. 3,
Jia, Tongxuan
Wang, Zujun
Xue, Yuanyuan
Jiao, Qianli
Yang, Xie
Nie, Xu
Lai, Shankun
Ma, Wuying
He, Baoping
and
Liu, Minbo
2021.
The influence of temperature and energy on defect evolution and clustering during cascade in GaAs.
Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms,
Vol. 502,
Issue. ,
p.
198.
Lovshenko, I. Yu.
Voronov, A. Yu.
Roshchenko, P. S.
Ternov, R. E.
Galkin, Ya. D.
Kunts, A. V.
Stempitsky, V. R.
and
Bi, Jinshun
2022.
The proton flux influence on electrical characteristics of a dual-channel hemt based on GaAs.
Doklady BGUIR,
Vol. 19,
Issue. 8,
p.
81.
Akkerman, A.
Barak, J.
and
Murat, M.
2022.
NIEL Calculations for III–V Compound Semiconductors Under Electron or Proton Irradiation.
IEEE Transactions on Nuclear Science,
Vol. 69,
Issue. 9,
p.
2056.
Böer, Karl W.
and
Pohl, Udo W.
2022.
Semiconductor Physics.
p.
1.
Debelle, A.
Gutierrez, G.
Boulle, A.
Monnet, I.
and
Thomé, L.
2022.
Effect of energy deposition on the disordering kinetics in dual-ion beam irradiated single-crystalline GaAs.
Journal of Applied Physics,
Vol. 132,
Issue. 8,
Olikh, Oleg
and
Lytvyn, Petro
2022.
Defect engineering using microwave processing in SiC and GaAs.
Semiconductor Science and Technology,
Vol. 37,
Issue. 7,
p.
075006.
Teunissen, Johannes L.
Jarrin, Thomas
Richard, Nicolas
Koval, Natalia E.
Santiburcio, Daniel Muñoz
Kohanoff, Jorge
Artacho, Emilio
Cleri, Fabrizio
and
Da Pieve, Fabiana
2023.
Effect of electronic stopping in molecular dynamics simulations of collision cascades in gallium arsenide.
Physical Review Materials,
Vol. 7,
Issue. 2,
Böer, Karl W.
and
Pohl, Udo W.
2023.
Semiconductor Physics.
p.
595.
Liu, Lixia
Qiu, Rongyang
Chen, Yangchun
Jiang, Mingxuan
Gao, Ning
Huang, Bowen
Gao, Fei
Hu, Wangyu
and
Deng, Huiqiu
2023.
Displacement cascades database from molecular dynamics simulations in tungsten.
Journal of Nuclear Materials,
Vol. 580,
Issue. ,
p.
154415.
Zhao, Siqin
and
Xiao, Haiyan
2024.
Ab initio molecular dynamics simulation of low-energy displacement events in Sb2Se3.
The European Physical Journal Plus,
Vol. 139,
Issue. 7,
Anderson, Sean
Khafizov, Marat
and
Chernatynskiy, Aleksandr
2024.
Threshold displacement energies and primary radiation damage in AlN from molecular dynamics simulations.
Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms,
Vol. 547,
Issue. ,
p.
165228.
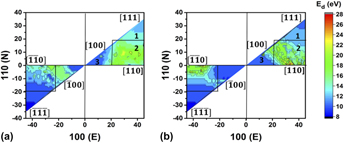
 $E_{\rm{d}}^{{\rm{min}}}$
, is found to be 8 eV, but the maxima,
$E_{\rm{d}}^{{\rm{min}}}$
, is found to be 8 eV, but the maxima,
 $E_{\rm{d}}^{{\rm{max}}}$
, are 22 and 28 eV for Ga and As, respectively. The distribution of E
d within unit stereographic triangles indicates that E
d shows a weak dependence on the recoil directions, in contrast to other semiconductors. The average threshold displacement energy is 13 ± 1 eV, which is in excellent agreement with available experiments.
$E_{\rm{d}}^{{\rm{max}}}$
, are 22 and 28 eV for Ga and As, respectively. The distribution of E
d within unit stereographic triangles indicates that E
d shows a weak dependence on the recoil directions, in contrast to other semiconductors. The average threshold displacement energy is 13 ± 1 eV, which is in excellent agreement with available experiments.