Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-23T06:51:53.658Z Has data issue: false hasContentIssue false
  • English
  • Français

Composition-dependent hardness and Young’s modulus in fcc Ni–X (X = Rh, Ta, W, Re, Os, and Ir) alloys: Experimental measurements and CALPHAD modeling

Published online by Cambridge University Press:  16 July 2019

Juan Chen  and
Lijun Zhang Open the ORCID record for Lijun Zhang [Opens in a new window]
Juan Chen*
Affiliation:
Testing Center, Yangzhou University, Yangzhou 225009, People’s Republic of China; and School of Chemistry and Chemical Engineering, Yangzhou University, Yangzhou 225009, China
Lijun Zhang*
Affiliation:
State Key Laboratory of Powder Metallurgy, Central South University, Changsha, Hunan 410083, People’s Republic of China
*
a)Address all correspondence to these authors. e-mail: [email protected]
b)e-mail: [email protected]
Get access

Abstract

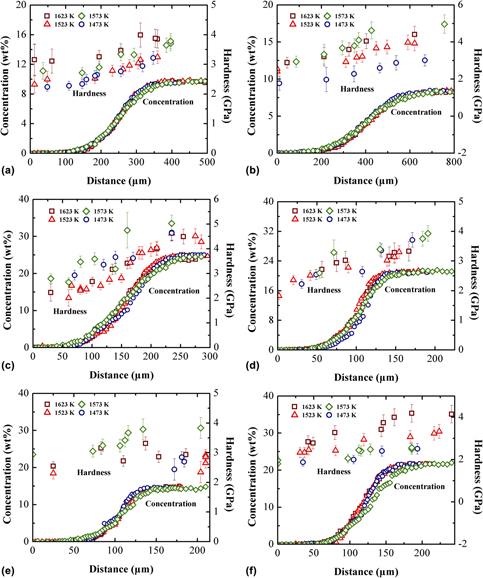
In this paper, the hardness and Young’s moduli along the diffusion paths in fcc Ni–X (X = Rh, Ta, W, Re, Os, and Ir) binary diffusion couples were measured by using the nanoindentation technique. Hardness increases gradually from the pure Ni to the fcc Ni–X alloys, except for the Ni–Os system. While the Young’ moduli in fcc Ni–X alloys scatter much larger and do not show noticeable variation with the addition of element X. After that, the CALPHAD models for description of the composition-dependent hardness and Young’s modulus were proposed, and an in-house code was developed. Based on the present experimental data, the CALPHAD-type descriptions for hardness and Young’s modulus in fcc Ni–X (X = Rh, Ta, W, Re, Os, and Ir) systems were obtained. The model-predicted hardness and Young’s moduli of composition dependence agree with the experimental data in general. It is anticipated that the presently obtained CALPHAD-type hardness and Young’s modulus descriptions, together with the previous thermodynamic and atomic mobility databases, can be used for the future alloy design of novel Ni-based superalloys.

Keywords

Ni–X (X = Rh, Ta, W, Re, Os, and Ir) alloyshardnessYoung’s modulusCALPHAD
Type
Article
Information
Journal of Materials Research , Volume 34 , Issue 18 , 30 September 2019 , pp. 3104 - 3115
Copyright
Copyright © Materials Research Society 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Rakoczy, Ł., Cempura, G., Kruk, A., Czyrska-Filemonowicz, A., and Zielińska-Lipiec, A.: Evolution of γ′ morphology and γ/γ′ lattice parameter misfit in a nickel-based superalloy during non-equilibrium cooling. J. Mater. Res. 110, 66 (2019).Google Scholar
Huo, M., Liu, L., Yang, W.C., Li, Y.F., Hu, S.S., Su, H.J., Zhang, J., and Fu, H.Z.: Formation of low-angle grain boundaries under different solidification conditions in the rejoined platforms of Ni-based single crystal superalloys. J. Mater. Res. 34, 251 (2019).CrossRefGoogle Scholar
Sun, W.J., Kothari, S., and Sun, C.C.: The relationship among tensile strength, Young’s modulus, and indentation hardness of pharmaceutical compacts. Powder Technol. 331, 1 (2018).CrossRefGoogle Scholar
Liu, M., Lin, J.Y., Lu, C., Tieu, K.A., Zhou, K., and Koseki, T.: Progress in indentation study of materials via both experimental and numerical methods. Crystals 7, 258 (2017).CrossRefGoogle Scholar
Zhao, J.C., Jackson, M.R., Peluso, L.A., and Brewer, L.N.: A diffusion-multiple approach for mapping phase diagrams, hardness, and elastic modulus. JOM 54, 42 (2002).CrossRefGoogle Scholar
You, L. and Song, X.P.: First principles study of low Young’s modulus Ti–Nb–Zr alloy system. Mater. Lett. 80, 165 (2012).CrossRefGoogle Scholar
Hu, R.M., Zhou, Z.B., Zhou, X.L., Yu, J., and Zhang, K.H.: Phase stability, electronic structure, elastic properties and hardness of Ru–Ir alloys: First-principles calculations. Mater. Res. Express 4, 076512 (2017).CrossRefGoogle Scholar
Li, X., Tu, X.Q., Liu, B.Q., Song, J.M., Luo, W., Lei, Y., Sun, G.A., Chen, B., and Hu, Q.M.: Composition-dependent elastic properties in Ti–Ni–Nb from first principle calculations. J. Alloys Compd. 706, 260 (2017).CrossRefGoogle Scholar
Wen, S.Y., Tang, Y., Zhong, J., Zhang, L.J., Du, Y., and Zheng, F.: High-throughput measurements of interdiffusivity matrices in face centered cubic Ni–Al–Mo alloys at 1273–1473 K. J. Mater. Res. 32, 2188 (2017).CrossRefGoogle Scholar
Chen, J., Zhang, C., Wang, J., Chen, W.M., Tang, Y., Zhang, L.J., and Du, Y.: Thermodynamic description, diffusivities and atomic mobilities in binary Ni–Os system. Calphad 50, 118 (2015).CrossRefGoogle Scholar
Kaufman, L. and Bernstein, H.: Computer Calculation of Phase Diagrams (Academic Press, New York, 1970).Google Scholar
Zhang, L.J., Wang, J., Du, Y., Hu, R., Nash, P., Lu, X.G., and Jiang, C.: Thermodynamic properties of the Al–Fe–Ni system acquired via a hybrid approach combining calorimetry, first-principles and CALPHAD. Acta Mater. 57, 5324 (2009).CrossRefGoogle Scholar
Zhang, L.J., Du, Y., Steinbach, I., Chen, Q., and Huang, B.: Diffusivities of an Al–Fe–Ni melt and their effects on the microstructure during solidification. Acta Mater. 58, 3664 (2010).CrossRefGoogle Scholar
Available at: https://www.thermocalc.com/products-services/databases (accessed April 10, 2019).Google Scholar
Liu, Z.K., Zhang, H., Ganeshan, S., Wang, Y., and Mathaudhu, S.N.: Computational modeling of effects of alloying elements on elastic coefficients. Scr. Mater. 63, 686 (2010).CrossRefGoogle Scholar
Lu, X.G., Selleby, M., and Sundman, B.: Assessments of molar volume and thermal expansion for selected bcc, fcc and hcp metallic elements. Calphad 29, 68 (2005).CrossRefGoogle Scholar
Gheribi, A.E. and Chartrand, P.: Application of the CALPHAD method to predict the thermal conductivity in dielectric and semiconductor crystals. Calphad 39, 70 (2012).CrossRefGoogle Scholar
Liu, X.T. and Oikawa, K.: Assessment of the temperature and pressure dependence of molar volume and phase diagrams of Cu and Zn. Calphad 47, 114 (2014).CrossRefGoogle Scholar
Zhang, L.J., Stratmann, M., Du, Y., Sundman, B., and Steinbach, I.: Incorporating the CALPHAD sublattice approach of ordering into the phase-field model with finite interface dissipation. Acta Mater. 88, 156 (2015).CrossRefGoogle Scholar
Chen, J., Zhang, L.J., and Lu, X.G.: Screening of possible Re-substitutional elements in single-crystal Ni-based superalloys: A viewpoint from interdiffusion coefficients in Ni–Al–X ternaries. Metall. Mater. Trans. A 49A, 2999 (2018).CrossRefGoogle Scholar
Chen, J., Xiao, J.K., Zhang, L., and Du, Y.: Interdiffusion in fcc Ni–X (X = Rh, Ta, W, Re, and Ir) alloys. J. Alloys Compd. 657, 457 (2016).CrossRefGoogle Scholar
Lin, Y., Wei, M., Li, G.D., and Zhang, L.J.: Phase equilibria and microhardness of as-cast and annealed Ni–Al–Os alloys in Ni-rich region. J. Phase Equilib. Diffus. 39, 944 (2018).CrossRefGoogle Scholar
Chen, J., Zhao, J.R., Zhang, L.J., Lu, X-G., and Liu, L.: Atomic mobilities in fcc Ni-rich Ni–X (X = Rh, Ta, W, Re, and Ir) systems. Calphad 65, 316 (2019).CrossRefGoogle Scholar
Zhou, S.H., Wang, Y., Chen, L.Q., Liu, Z.K., and Napolitano, R.E.: Solution-based thermodynamic modeling of the Ni–Ta and Ni–Mo–Ta systems using first-principle calculations. Calphad 33, 631 (2009).CrossRefGoogle Scholar
Gustafson, P.: A thermodynamic evaluation of the Cr–Ni–W system. Calphad 12, 277 (1988).CrossRefGoogle Scholar
Yaqoob, K. and Joubert, J.M.: Experimental determination and thermodynamic modeling of the Ni–Re binary system. J. Solid State Chem. 196, 320 (2012).CrossRefGoogle Scholar
Durst, K., Franke, O., Böhner, A., and Göken, M.: Indentation size effect in Ni–Fe solid solutions. Acta Mater. 55, 6825 (2007).CrossRefGoogle Scholar
Schwaiger, R., Moser, B., Dao, M., Chollacoop, N., and Suresh, S.: Some critical experiments on the strain-rate sensitivity of nanocrystalline nickel. Acta Mater. 51, 5159 (2003).CrossRefGoogle Scholar
Wang, C.H., Fang, T.H., Cheng, P.C., Chiang, C.C., and Chao, K.C.: Simulation and experimental analysis of nanoindentation and mechanical properties of amorphous NiAl alloys. J. Mol. Model. 21, 1 (2015).CrossRefGoogle ScholarPubMed
Petley, V., Sathishkumar, S., Raman, K.H.T., Rao, G.M., and Chandrasekhar, U.: Microstructural and mechanical characteristics of Ni–Cr thin films. Mater. Res. Bull. 66, 59 (2015).CrossRefGoogle Scholar
Kim, S.H.: Young’s Modulus Measurement of Electroplated Nickel Using AFM (2006 ASME International Mechanical Engineering Congress and Exposition, Chicago, Illinois, 2006).CrossRefGoogle Scholar
Hubert, O., Milhet, X., Gadaud, P., Tatat, M., Renault, P.O., and Coupeau, C.: Modeling of Young’s modulus variations with temperature of Ni and oxidized Ni using a magneto-mechanical approach. Mater. Sci. Eng., A 633, 76 (2015).CrossRefGoogle Scholar
Köster, W.: Temperaturabhangigkeit des Elastizitatsmoduls reiner Metalle. Z. Metallkd. 39, 1 (1948).Google Scholar
Honda, K. and Terada, T.: On the change of elastic constants of ferromagnetic substances by magnetization. Tokyo Sugaku-Butsurigakukwai Kiji-Gaiyo 2, 381 (1905).Google Scholar
Kurnakow, N. and Rapke, J.: Harte und Elastizitatsmodul isomorpher Gemische von Kupfer mit Nickel. Z. Anorg. Chem. 87, 269 (1914).CrossRefGoogle Scholar
Mudge, W.A. and Luff, L.W.: Some mechanical properties of nickel, manganese–nickel and copper–nickel alloys. Am. Soc. Test. Mater., Proc. 28, 278 (1928).Google Scholar
Jacquerod, A. and Mügeli, H.: Etude sur l’élasticité de flexion: Fer – cuivre – or – argent – platine – verre de silice – nickel. Helv. Phys. Acta 4, 3 (1931).Google Scholar
Nakamura, K.: Unterschung der Variationen des Elastizitatskoeffizienten der Metallegierung Ni–Fe durch Magnetisierung. Z. Phys. 94, 707 (1935).CrossRefGoogle Scholar
Davies, R.M. and Thomas, I.H.: A dynamical method for the measurement of Young’s modulus for imperfectly elastic metals, and the application of the method to nickel and some of its alloys. Philos. Mag. 23, 361 (1937).CrossRefGoogle Scholar
Engler, O.: Der Elastizitätsmodul ferromagnetischer Stoffe in Abhängigkeit von der Temperatur und vom Magnetfeld. Ann. Phys. 423, 145 (1938).CrossRefGoogle Scholar
Kimura, R.I.: On the elastic moduli of ferromagnetic materials. Part I. Dynamical measurements of the elastic moduli of iron crystals. Proc. Phys.-Math. Soc. Jpn. 21, 686 (1939).Google Scholar
Yamamoto, M.: Young’s modulus of elasticity and its variation with magnetization in ferromagnetic nickel–copper alloys. Nippon Kinzoku Gakkaishi 6, 249 (1942).Google Scholar
Yamamoto, M.: On the ΔE-effect of iron, nickel and cobalt. Nippon Kinzoku Gakkaishi 5, 167 (1941).Google Scholar
Masumoto, H. and Saito, H.: On elasticity, its temperature coefficient, and heat expansion coefficient of the nickel–copper alloy system. Nippon Kinzoku Gakkaishi 8, 49 (1944).Google Scholar
Ledbetter, H. M. and Reed, R. P.: Elastic properties of metals and alloys. I. Iron, Nickel, and Iron–Nickel Alloys. J. Phys. Chern. Ref. Data 2, 531 (1973).Google Scholar
Pavlov, V.A., Kriutchkov, N.F., and Fedotov, I.D.: Relationship of temperature to elastic modulus in nickel–copper alloys. Phys. Met. Metallogr. 5, 160 (1957).Google Scholar
Hill, W.H., Shimmin, K.D., and Wilcox, B.A.: Elevated temperature dynamic moduli of metallic materials. Am. Soc. Test. Mater., Proc. 61, 890 (1961).Google Scholar
Tino, Y. and Maeda, T.: On the anomalous thermoelastic variation in the invar-type iron–nickel alloys. J. Phys. Soc. Jpn. 18, 955 (1963).CrossRefGoogle Scholar
Orlov, A.F. and Fedotov, S.G.: Temperature dependence of the Young’s and shear moduli of Ni–Cu alloys. Phys. Met. Metallogr. 22, 146 (1966).Google Scholar
Faninger, G.: Die elastischen konstanten von Kupfer·Nickel-Vielkristallen. Z. Metallkd. 60, 601 (1969).Google Scholar
Masumoto, H., Saitô, H., and Sawaya, S.: Thermal expansion and temperature dependence of Young’s modulus of nickel-copper alloys. Trans. Jpn. Inst. Met. 11, 88 (1970).CrossRefGoogle Scholar
Merker, J., Lupton, D., Töpfer, M., and Knake, H.: High temperature mechanical properties of the platinum group metals. Platinum Met. Rev. 45, 74 (2001).Google Scholar
Shang, S.L., Saengdeejing, A., Mei, Z.G., Kim, D.E., Zhang, H., Ganeshan, S., Wang, Y., and Liu, Z.K.: First-principles calculations of pure elements: Equations of state and elastic stiffness constants. Comput. Mater. Sci. 48, 813 (2010).CrossRefGoogle Scholar
Shang, S.L., Kim, D.E., Zacherl, C.L., Wang, Y., Du, Y., and Liu, Z.K.: Effects of alloying elements and temperature on the elastic properties of dilute Ni-base superalloys from first-principles calculations. J. Appl. Phys. 112, 053515 (2012).CrossRefGoogle Scholar
Kim, D., Shang, S.L., and Liu, Z.K.: Effects of alloying elements on elastic properties of Ni by first-principles calculations. Comput. Mater. Sci. 47, 254 (2009).CrossRefGoogle Scholar
Hill, R.: The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc., London, Sect. A 65, 349 (1952).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).CrossRefGoogle Scholar
Oliver, W.C. and Pharr, G.M.: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19, 3 (2004).CrossRefGoogle Scholar