Published online by Cambridge University Press: 07 October 2020
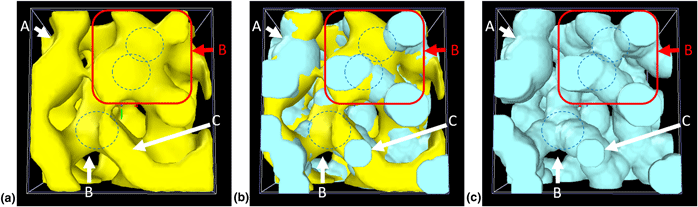
Soyarslan et al. [J. Mater. Res. 33(20), 3371 (2018)] proposed a beam-finite element model for the computation of effective elastic properties of nanoporous materials, where the ligament diameter along the skeleton is determined with the biggest sphere algorithm. Although this algorithm is often used in the literature, it is known that it systematically overestimates the diameter in network structures. Thus, the need for further stiffening of the junction zones as proposed by the authors is in contradiction to the literature. Furthermore, the factor 40 appears to be one order of magnitude too high. We show that the 3D microstructures generated from random Gaussian fields contain features that are violating the assumption of circular cross-sections and, therefore, cannot be captured by the biggest sphere algorithm. Consequently, the authors required an unphysically high value of 40 to compensate this hidden effect.