Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-05T16:22:24.176Z Has data issue: false hasContentIssue false
  • English
  • Français

Calculation of solid–liquid interfacial free energy of silicon based on classical nucleation theory

Published online by Cambridge University Press:  05 December 2016

L.K. Wu ,
Q.L. Li ,
B. Xu  and
W. Liu
L.K. Wu
Affiliation:
Key Laboratory of Advanced Materials of Education of China, Tsinghua University, Beijing 100084, China; and School of Material Science and Engineering, Tsinghua University, Beijing 100084, China
Q.L. Li
Affiliation:
Key Laboratory of Advanced Materials of Education of China, Tsinghua University, Beijing 100084, China; School of Material Science and Engineering, Tsinghua University, Beijing 100084, China; and Graduate School at Shenzhen, Tsinghua University, Shenzhen, China
B. Xu*
Affiliation:
Key Laboratory of Advanced Materials of Education of China, Tsinghua University, Beijing 100084, China; and School of Material Science and Engineering, Tsinghua University, Beijing 100084, China
W. Liu*
Affiliation:
Key Laboratory of Advanced Materials of Education of China, Tsinghua University, Beijing 100084, China; and School of Material Science and Engineering, Tsinghua University, Beijing 100084, China
*
a) Address all correspondence to these authors. e-mail: [email protected]
b) e-mail: [email protected]
Get access

Abstract

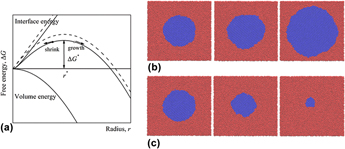
The solid–liquid interfacial free energy of silicon was calculated by the method based on classical nucleation theory (CNT), where the molecular dynamic (MD) simulations were carried out, and a series of cylindrical solid nuclei were equilibrated with undercooled liquid phase to create an ideal model of a homogeneous nucleation. The interfacial free energy was extracted from the relationship between the critical nuclei radii and their corresponding equilibrium temperatures. The influence of the interfacial curvature on its free energy was for the first time considered in our work, the influence can be measured by a Tolman length which was introduced to modify the traditional CNT; therefore, more accurate results were obtained. The averaged melting point and Tolman length extracted from simulations were 1678.27 K and 2.82 Å, respectively, which are consistent with the expected results. The averaged interfacial free energy is 401.92 mJ/m2, which is in good agreement with the results from experiments.

Keywords

interfacial free energyclassical nucleation theorycurvature
Type
Articles
Information
Journal of Materials Research , Volume 31 , Issue 23 , 14 December 2016 , pp. 3649 - 3656
Check for updates
Copyright
Copyright © Materials Research Society 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Turnbull, D. and Fisher, J.C.: Rate of nucleation in condensed systems. J. Chem. Phys. 17, 71 (1949).CrossRefGoogle Scholar
Turnbull, D.: Formation of crystal nuclei in liquid metals. J. Appl. Phys. 21, 1022 (1950).CrossRefGoogle Scholar
Turnbull, D. and Cech, R.E.: Microscopic observation of the solidification of small metal droplets. J. Appl. Phys. 21, 804 (1950).CrossRefGoogle Scholar
Turnbull, D.: Kinetics of solidification of supercooled liquid mercury droplets. J. Chem. Phys. 20, 411 (1952).CrossRefGoogle Scholar
Kelton, K.F.: Crystal nucleation in liquids and glasses. Solid State Phys. 45, 75 (1991).CrossRefGoogle Scholar
Kelton, K.F.: Crystal nucleation in supercooled liquid metals. Int. J. Microgravity Sci. Appl. 30, 11 (2013).Google Scholar
Herlach, D.M., Gao, J., Holland-Moritz, D., and Volkmann, T.: Nucleation and phase-selection in undercooled melts. Mater. Sci. Eng., A 375, 9 (2004).Google Scholar
Gündüz, M. and Hunt, J.D.: The measurement of soild–liquid surface energies in the Al–Cu, Al–Si and Pb–Sn systems. Acta Metall. 33, 1651 (1985).Google Scholar
Broughton, J.Q. and Gilmer, G.H.: Molecular dynamics investigation of the crystal–fluid interface. VI. Excess surface free energies of crystal–liquid systems. J. Chem. Phys. 84, 5759 (1986).Google Scholar
Hoyt, J.J., Asta, M., and Karma, A.: Method for computing the anisotropy of the solid–liquid interfacial free energy. Phys. Rev. Lett. 86, 5530 (2001).Google Scholar
Bai, X.M. and Li, M.: Calculation of solid–liquid interfacial free energy: A classical nucleation theory based approach. J. Chem. Phys. 124, 124707 (2006).Google Scholar
Zhou, H., Lin, X., Wang, M., and Huang, W.: Calculation of solid–liquid interfacial free energy of Cu by two different methods. J. Cryst. Growth. 377, 107 (2013).Google Scholar
Liu, J., Dacidchack, R.L., and Dong, H.B.: Molecular dynamics calculation of solid–liquid interfacial free energy and its anisotropy during iron solidification. Comput. Mater. Sci. 74, 92 (2013).Google Scholar
Hashimoto, R., Shibuta, Y., and Suzuki, T.: Estimation of solid–liquid interfacial energy from Gibbs–Thomson effect: A molecular dynamics study. ISIY Int. 51, 1664 (2011).CrossRefGoogle Scholar
Porter, D.A. and Easterling, K.E.: Phase transformations in metals and alloys, 2nd ed. (Chapman & Hall, London, 1992).CrossRefGoogle Scholar
Tolman, R.C.: The effect of droplet size on surface tension. J. Chem. Phys. 17, 333 (1949).Google Scholar
Haye, M.J. and Bruin, C.: Molecular dynamics study of the curvature correction to the surface tension. J. Chem. Phys. 100, 556 (1994).CrossRefGoogle Scholar
Kashchiev, D.: Nucleation: Basic theory with applications (Butterworth-Heinemann, Oxford, 2000).Google Scholar
Bai, X.M. and Li, M.: Nature and extent of melting in superheated solids: Liquid-solid coexistence model. Phys. Rev. B: Condens. Matter Mater. Phys. 72, 052108 (2005).CrossRefGoogle Scholar
Stillinger, F.H. and Weber, T.A.: Computer simulation of local order in condensed phases of silicon. Phys. Rev. B: Condens. Matter Mater. Phys. 31, 5262 (1985).CrossRefGoogle ScholarPubMed
Morris, J.R.: Complete mapping of the anisotropic free energy of the crystal-melt interface in Al. Phys. Rev. B: Condens. Matter Mater. Phys. 66, 144104 (2002).Google Scholar
Buta, D., Asta, M., and Hoyt, J.J.: Kinetic coefficient of steps at the Si(111) crystal-melt interface from molecular dynamics simulations. J. Chem. Phys. 127, 074703 (2007).Google Scholar
Tang, Y.W., Wang, J., and Zeng, X.C.: Molecular simulations of solid–liquid interfacial tension of silicon. J. Chem. Phys. 124, 236103 (2006).CrossRefGoogle ScholarPubMed
Stiffler, S.R., Thompson, M.O., and Peercy, P.S.: Supercooling and nuceation of silicon after laser melting. Phys. Rev. Lett. 60, 2519 (1988).Google Scholar
Liu, R.P., Volkmann, T., and Herlach, D.M.: Undercooling and Solidification of Si by electromagnetic levitation. Acta Mater. 49, 439 (2001).Google Scholar
Shao, Y. and Spaepen, F.: Undercooling of bulk liquid silicon in an oxide flux. J. Appl. Phys. 79, 2981 (1996).Google Scholar
Apte, P.A. and Zeng, X.C.: Anisotropy of crystal-melt interfacial free energy of silicon by simulation. Appl. Phys. Lett. 92, 221903 (2008).CrossRefGoogle Scholar
Morris, J.R., Wang, C.Z., Ho, K.M., and Chan, C.T.: Melting line of aluminum from simulations of coexisting phases. Phys. Rev. B: Condens. Matter Mater. Phys. 49, 3109 (1994).Google Scholar
Morris, J.R. and Song, X.Y.: The melting lines of model systems calculated from coexistence simulations. J. Chem. Phys. 116, 9352 (2002).Google Scholar
Broughton, J.Q. and Gilmer, G.H.: Interface melting: Simulations of surfaces and grain boundaries at high temperatures. J. Phys. Chem. 91, 6347 (1987).Google Scholar
Hoyt, J.J., Olmsted, D., Jindal, S., Asta, M., and Karma, A.: Method for computing short-range forces between solid-liquid interfaces driving grain boundary premelting. Phys. Rev. E 79, 020601 (2009).CrossRefGoogle ScholarPubMed
Kikuchi, R. and Cahn, J.W.: Grain-boundary melting transition in a two-dimensional lattice-gas model. Phys. Rev. B: Condens. Matter Mater. Phys. 21, 1893 (1980).Google Scholar