Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-27T00:36:10.777Z Has data issue: false hasContentIssue false
  • English
  • Français

The size effect in the mechanical strength of semiconductors and metals: Strain relaxation by dislocation-mediated plastic deformation

Published online by Cambridge University Press:  11 August 2017

David J. Dunstan
David J. Dunstan*
Affiliation:
School of Physics and Astronomy, Queen Mary University of London, London E1 4NS, U.K.
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

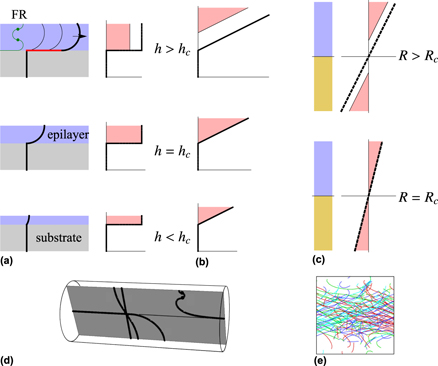
The Ph.D. work of Jan H. van der Merwe in 1949 established a new paradigm for the understanding of dislocation dynamics in restricted volumes. This led to a comprehensive understanding of plasticity, or strain relaxation, in the context of strained-layer semiconductor structures. However, this understanding was largely overlooked in the context of traditional metallurgy and micromechanics. We identify four reasons for this, the apparent need for an unstrained substrate in van der Merwe’s theory, the supposed inapplicability to strain gradients, the supposed inapplicability to the Hall–Petch effect (dependence of strength on the inverse square root of grain size), and an emphasis on understanding strain hardening rather than the yield point. Addressing these four points in particular, here it is shown how the insights of van der Merwe and of the earlier work by Lawrence Bragg lead to a coherent and unified view of the size-effect phenomena ranging from the Hall–Petch effect to the strain-gradient plasticity theory.

Keywords

dislocationsstress/strain relationshipgrain size
Type
Invited Reviews
Information
Journal of Materials Research , Volume 32 , Issue 21: Focus Issue: Jan van der Merwe: Epitaxy and the Computer Age , 14 November 2017 , pp. 4041 - 4053
Check for updates
Copyright
Copyright © Materials Research Society 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Contributing Editor: Artur Braun

This section of Journal of Materials Research is reserved for papers that are reviews of literature in a given area.

References

REFERENCES

Volterra, V.: Sur l’équilibre des corps élastiques multiplement connexes. Ann. Sci. École Norm. Sup. 24, 401 (1907).CrossRefGoogle Scholar
Taylor, G.I.: The mechanism of plastic deformation of crystals. Part I. Theoretical. Proc. R. Soc. London, Ser. A 145, 362 (1934).Google Scholar
Orowan, E.: Zur Kristallplastizität. III. Über den Mechanismus des Gleitvorganges. Z. Phys. 89, 634 (1934).Google Scholar
Polanyi, M.: Über eine Art Gitterstörung, die einen Kristall plastisch machen könnte. Z. Phys. 89, 660 (1934).Google Scholar
Frank, F.C. and van der Merwe, J.H.: One-dimensional dislocations. II. Misfitting monolayers and oriented overgrowth. Proc. R. Soc. London, Ser. A 198, 216 (1949).Google Scholar
van der Merwe, J.H.: Misfitting monolayers and oriented overgrowths. Discuss. Faraday Soc. 5, 201 (1949).Google Scholar
Li, Y., Bushby, A.J., and Dunstan, D.J.: The Hall–Petch effect as a manifestation of the general size effect. Proc. R. Soc. A 472, 20150890 (2016).Google Scholar
Bragg, W.L.: A theory of the strength of metals. Nature 149, 511 (1942).Google Scholar
Hall, E.O.: The deformation and ageing of mild steel: III discussion of results. Proc. R. Soc. B 64, 747 (1951).Google Scholar
Petch, N.J.: The cleavage strength of polycrystals. J. Iron Steel Inst. 174, 25 (1953).Google Scholar
Kelly, A.: Lawrence Bragg’s interest in the deformation of metals and 1950–1953 in the Cavendish—A worm’s-eye view. Acta Crystallogr., Sect. A: Found. Crystallogr. 69, 16 (2013).Google Scholar
Bragg, W.L.: The strength of metals. Math. Proc. Cambridge Philos. Soc. 45, 125 (1949).Google Scholar
Kuhlmann-Wilsdorf, D.: The impact of F.R.N. Nabarro on the LEDS theory of workhardening. Prog. Mater. Sci. 54, 707 (2009).CrossRefGoogle Scholar
Matthews, J.W. and Crawford, J.L.: Accomodation of misfit between single-crystal films of nickel and copper. Thin Solid Films 5, 187 (1970).CrossRefGoogle Scholar
Matthews, J.W. and Jesser, W.A.: Experimental evidence for pseudomorphic growth of platinum on gold. Acta Metall. 15, 595 (1967).Google Scholar
Matthews, J.W. and Klokholm, E.: Fracture of brittle epitaxial films under the influence of misfit stress. Mater. Res. Bull. 7, 213 (1972).Google Scholar
Matthews, J.W. and Blakeslee, A.E.: Defects in epitaxial multilayers: I. Misfit dislocations. J. Cryst. Growth 27, 118 (1974).Google Scholar
Available at: http://www.manchester.ac.uk/discover/news/two-university-of-manchester-discoveries-in-the-top-ten-of-all-time (accessed March 31, 2017).Google Scholar
People, R. and Bean, J.C.: Calculation of critical layer thickness versus lattice mismatch for Ge x Si1−x /Si strained-layer heterostructures. Appl. Phys. Lett. 47, 322 (1985).CrossRefGoogle Scholar
Drigo, A.V., Aydinli, A., Carnera, A., Genova, F., Rigo, C., Ferrari, C., Franzosi, P., and Salviati, G.: On the mechanisms of strain release in molecular-beam-epitaxy-grown In x Ga1−x As/GaAs single heterostructures. J. Appl. Phys. 66, 1975 (1989).Google Scholar
Dunstan, D.J.: Strain and strain relaxation in semiconductors. J. Mater. Sci.: Mater. Electron. 8, 337 (1997).Google Scholar
Eshelby, J.D., Frank, F.C., and Nabarro, F.R.N.: The equilibrium of linear arrays of dislocations. Philos. Mag. 42, 351 (1951).Google Scholar
van der Merwe, J.H.: Strains in crystalline overgrowths. Philos. Mag. 7, 1433 (1962).CrossRefGoogle Scholar
Kuhlmann-Wilsdorf, D. and van der Merwe, J.H.: Theory of dislocation cell sizes in deformed metals. Mater. Sci. Eng. 55, 79 (1982).Google Scholar
Nix, W.D.: Mechanical properties of thin films. Metall. Trans. A 20, 2217 (1989).Google Scholar
Thompson, C.V.: The yield stress of polycrystalline thin films. J. Mater. Res. 8, 237 (1993).Google Scholar
Unwin, W.C.: The Testing of Materials of Construction (Longmans, Green, and Co., London, 1888).Google Scholar
Brenner, S.S.: Tensile strength of whiskers. J. Appl. Phys. 27, 1484 (1956).Google Scholar
Uchic, M.D., Dimiduk, D.M., Florando, J.N., and Nix, W.D.: Sample dimensions influence strength and crystal plasticity. Science 305, 986 (2004).Google Scholar
Korte, S. and Clegg, W.J.: Discussion of the dependence of the effect of size on the yield stress in hard materials studied by microcompression of MgO. Philos. Mag. 91, 1150 (2010).Google Scholar
Fleck, N.A., Muller, G.M., Ashby, M.F., and Hutchinson, J.W.: Strain gradient plasticity: Theory and experiment. Acta Metall. Mater. 42, 475 (1994).Google Scholar
Stölken, J.S. and Evans, A.G.: A microbend test method for measuring the plasticity length scale. Acta Mater. 46, 5109 (1998).Google Scholar
Ashby, M.F.: The deformation of plastically non-homogeneous materials. Philos. Mag. 21, 399 (1970).Google Scholar
Li, J.M.C.: Petch relation and grain boundary sources. Trans. TMS 227, 239 (1963).Google Scholar
Conrad, H.: Effect of grain size on the lower yield and flow stress on iron and steel. Acta Metall. 11, 75 (1963).Google Scholar
Zhang, X. and Aifantis, K.: Interpreting the internal length scale in strain gradient plasticity. Rev. Adv. Mater. Sci. 41, 72 (2015).Google Scholar
Nix, W.D. and Gao, H.J.: Indentation size effects in crystalline materials: A law for strain gradient plasticity. J. Mech. Phys. Solids 46, 411 (1998).Google Scholar
Evans, A.G. and Hutchinson, J.W.: A critical assessment of theories of strain gradient plasticity. Acta Mater. 57, 1675 (2009).Google Scholar
Beanland, R.: Dislocation multiplication mechanisms in low-misfit strained epitaxial layers. J. Appl. Phys. 77, 6217 (1995).Google Scholar
Dunstan, D.J., Ehrler, B., Bossis, R., Joly, S., P’ng, K.M.Y., and Bushby, A.J.: Elastic limit and strain-hardening of thin wires in torsion. Phys. Rev. Lett. 103, 155501 (2009).Google Scholar
Shan, Z.W., Mishra, R.K., Syed Asif, S.A., Warren, O.L., and Minor, A.M.: Mechanical annealing and source-limited deformation in submicrometre-diameter Ni crystals. Nat. Mater. 7, 115 (2007).Google Scholar
Greer, J.R. and Nix, W.D.: Nanoscale gold pillars strengthened through dislocation starvation. Phys. Rev. B 73, 245410 (2006).Google Scholar
Tersoff, J.: Dislocations and strain relief in compositionally graded layers. Appl. Phys. Lett. 62, 693 (1993).Google Scholar
Motz, C. and Dunstan, D.J.: Observation of the critical thickness phenomenon in dislocation dynamics simulation of microbeam bending. Acta Mater. 60, 1603 (2012).CrossRefGoogle Scholar
Fleck, N.A. and Hutchinson, J.W.: A phenomenological theory for strain gradient effects in plasticity. J. Mech. Phys. Solids 41, 1825 (1993).CrossRefGoogle Scholar
Aifantis, E.C.: The physics of plastic deformation. Int. J. Plast. 3, 211 (1987).CrossRefGoogle Scholar
Dunstan, D.J.: Validation of a phenomenological strain-gradient plasticity theory. Philos. Mag. Lett. 96, 305 (2016).Google Scholar
Liu, D. and Dunstan, D.J.: Material length scale of strain gradient plasticity: A physical interpretation. Int. J. Plast. (2017). (in press).CrossRefGoogle Scholar
Dunstan, D.J. and Bushby, A.J.: The scaling exponent in the size effect of small scale plastic deformation. Int. J. Plast. 40, 152 (2013).CrossRefGoogle Scholar
Baldwin, W.M.: Yield strength of metals as a function of grain size. Acta Metall. 6, 139 (1958).Google Scholar
Aldrich, J.W. and Armstrong, R.W.: The grain size dependence of the yield, flow and fracture stress of commercial purity silver. Metall. Trans. 1, 2547 (1970).Google Scholar
Dunstan, D.J. and Bushby, A.J.: Grain size dependence of the strength of metals: The Hall–Petch effect does not scale as the inverse square root of grain size. Int. J. Plast. 53, 56 (2014).Google Scholar
Li, Y., Bushby, A.J., and Dunstan, D.J.: Quantitative explanation of the reported values of the Hall–Petch parameter. (unpublished).Google Scholar
Nissen, S.B., Magidson, T., Gross, K., and Bergstrom, C.T.: Publication bias and the canonization of false facts. eLife 5, e21451 (2016).Google Scholar
Narutani, T. and Takamura, J.: Grain-size strengthening in terms of dislocation density measured by resistivity. Acta Metall. Mater. 39, 2037 (1991).Google Scholar
Brown, L.M.: Indentation size effect and the Hall–Petch ‘law’. Mater. Sci. Forum 662, 13 (2011).Google Scholar
Argon, A.S.: Strengthening Mechanisms in Crystal Plasticity (Oxford University Press, Oxford, U.K. 2008); ch. 8.8.Google Scholar
Edwards, A.W.F.: Likelihood (Cambridge University Press, 1972; John Hopkins University Press, Baltimore, 1992).Google Scholar
Dong, D., Dunstan, D.J., and Bushby, A.J.: Plasticity and thermal recovery of thin copper wires in torsion. Philos. Mag. 95, 1739 (2015).Google Scholar
Walter, M. and Kraft, O.: A new method to measure torsion moments on small-scaled specimens. Rev. Sci. Instrum. 82, 035109 (2011).Google Scholar
Liu, D., He, Y., Dunstan, D.J., Zhang, B., Gan, Z., Hu, P., and Ding, H.: Anomalous plasticity in the cyclic torsion of micron scale metallic wires. Phys. Rev. Lett. 110, 244301 (2013).Google Scholar
Ehrler, B., Hou, X.D., Zhu, T.T., P’ng, K.M.Y., Walker, C.J., Bushby, A.J., and Dunstan, D.J.: Grain size and sample size interact to determine strength in a soft metal. Philos. Mag. 88, 3043 (2008).Google Scholar
Douthwaite, R.M.: Relationship between the hardness, flow stress, and grain size of metals. J. Iron Steel Inst. 208, 265 (1970).Google Scholar
Bei, H., Shim, S., Pharr, G.M., and George, E.P.: Effects of pre-strain on the compressive stress-strain response of Mo-alloy single-crystal micropillars. Acta Mater. 56, 4762 (2008).Google Scholar
Weiss, J., Ben Rhouma, W., Richeton, T., Dechanel, S., Louchet, F., and Truskinovsky, L.: From mild to wild fluctuations in crystal plasticity. Phys. Rev. Lett. 114, 105504 (2015).Google Scholar
Weinberger, C.R. and Cai, W.: Plasticity of metal wires in torsion: Molecular dynamics and dislocation dynamics simulations. J. Mech. Phys. Solids 58, 1011 (2010).Google Scholar
Brenchley, M.E., Hopkinson, M., Kelly, A., Kidd, P., and Dunstan, D.J.: Coherency strain as an athermal strengthening mechanism. Phys. Rev. Lett. 78, 3912 (1997).CrossRefGoogle Scholar
Kümmel, F., Kreuz, M., Hausöl, T., Höppel, H.W., and Göken, M.: Microstructure and mechanical properties of accumulative roll-bonded AA1050A/AA5005 laminated metal composites. Metals 6, 56 (2016).Google Scholar
Ritchie, R.O.: The conflicts between strength and toughness. Nat. Mater. 10, 817 (2011).Google Scholar
Gillin, W.P., Dunstan, D.J., Homewood, K.P., Howard, L.K., and Sealy, B.J.: Interdiffusion in InGaAs/GaAs quantum well structures as a function of depth. J. Appl. Phys. 73, 3782 (1993).CrossRefGoogle Scholar