Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-23T11:32:12.583Z Has data issue: false hasContentIssue false
  • English
  • Français

Modeling of exact viscoelastic stresses in bilayer systems due to thermal and/or lattice mismatch: Maxwell model

Published online by Cambridge University Press:  31 May 2011

Hsiang-Chun Hsueh ,
Donyau Chiang  and
Sanboh Lee
Hsiang-Chun Hsueh
Affiliation:
Department of Materials Science and Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
Donyau Chiang
Affiliation:
Instrument Technology Research Center, National Applied Research Laboratories, Hsinchu 30076, Taiwan
Sanboh Lee*
Affiliation:
Department of Materials Science and Engineering, National Tsing Hua University, Hsinchu 300, Taiwan
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

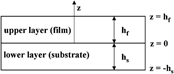
The exact solution of viscoelastic stresses in the bilayer system due to thermal and/or lattice mismatch is derived if both layers are Maxwell materials. When the thickness of one layer is much smaller than that of the other layer, the viscoelastic stresses in the bilayer system can be reduced to that of the thin film/substrate system. The relative film thickness and the position in the thin film/substrate systems are included in this solution. The average film stress decreases with increasing the normalized time and finally approaches zero in a long time. As the relative film thickness is equal to or less than 0.001, the average film stresses of the zeroth-order approximation, first-order approximation, and Hsueh and Lee model [J. Appl. Phys.91, 2760 (2002)] are close to that of exact solution. Nevertheless, as the relative film thickness is larger than 0.001, the accuracies of the zeroth-order approximation, first-order approximation, and Hsueh and Lee model are dependent on the normalized time and relative film thickness.

Keywords

SimulationThin filmThermal stresses
Type
Articles
Information
Journal of Materials Research , Volume 26 , Issue 11 , 14 June 2011 , pp. 1392 - 1398
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Sze, S.M.: Physics of Semiconductor Devices (Wiley, New York, 1969).Google Scholar
2.Maranowski, S.A., Kish, F.A., Caracci, S.J., Holonyak, N. Jr., Dallesasse, J.M., Bour, D.P., and Treat, D.W.: Native-oxide defined In0.5(AlxGa1−x)0.5P quantum well heterostructure window lasers (660 nm). Appl. Phys. Lett. 61, 1688 (1992).Google Scholar
3.Hsueh, C.H. and Evans, A.G.: Residual stresses in metal/ceramic bonded strips. J. Am. Ceram. Soc. 68, 241 (1985).Google Scholar
4.Townsend, P.H., Barnett, D.M., and Brunner, T.A.: Elastic relationships in layered composite media with approximation for the case of thin films on a thick substrate. J. Appl. Phys. 62, 4438 (1987).Google Scholar
5.Hsueh, C.H.: Some considerations of determination of residual stresses and Young’s moduli in ceramic coatings. J. Am. Ceram. Soc. 74, 1646 (1991).Google Scholar
6.Chuang, T.-J. and Lee, S.: Elastic flexure of bilayered beams subject to strain differentials. J. Mater. Res. 15, 2780 (2000).CrossRefGoogle Scholar
7.Shiue, S.T., Lin, H.C., Shen, T.Y., and Ouyang, H.: Residual stress measurement in carbon coatings of optical fibers from the fiber bending curvature and coating thickness difference. Appl. Phys. Lett. 86, 251910 (2005).Google Scholar
8.EerNisse, E.P.: Viscous flow of thermal SiO2. Appl. Phys. Lett. 30, 290 (1977).CrossRefGoogle Scholar
9.Liu, H.C. and Muraka, S.P.: Elastic and viscoelastic analysis of stress in thin films. J. Appl. Phys. 72, 3458 (1992).CrossRefGoogle Scholar
10.Volkert, C.A.: Stress and plastic flow in silicon during amorphization by ion bombardment. J. Appl. Phys. 70, 3521 (1991).Google Scholar
11.Volkert, C.A.: Density changes and viscous flow during structural relaxation of amorphous silicon. J. Appl. Phys. 74, 7107 (1993).Google Scholar
12.Isomae, S., Nanba, M., Tamaki, Y., and Maki, M.: Creep curve of silicon wafers. Appl. Phys. Lett. 30, 564 (1997).Google Scholar
13.Rosenberg, S.E., Wong, P.Y., and Miaoulis, I.N.: A theoretical study of the effect of thermal annealing on curvature changes in multilayered structures. Thin Solid Films 269, 64 (1995).CrossRefGoogle Scholar
14.Hsueh, C.H. and Lee, S.: Effects of viscous flow on residual stresses in film/substrate systems. J. Appl. Phys. 91, 2760 (2002).Google Scholar
15.Ko, S.C., Lee, S., and Hsueh, C.H.: Viscoelastic stress relaxation in film/substrate systems—Kelvin model. J. Appl. Phys. 93, 2453 (2003).Google Scholar
16.Zhang, X.C., Xu, B.S., Wang, H.D., and Wu, Y.X.: Residual stress relaxation in the film/substrate system due to creep deformation. J. Appl. Phys. 101, 083530 (2007).Google Scholar
17.Chen, Q.Q., Xuan, F.Z., and Tu, S.T.: Residual stress analysis in the film/substrate system with the effect of creep deformation. J. Appl. Phys. 106, 033512 (2009).Google Scholar
18.Hsueh, H.C., Chiang, D., and Lee, S.: Modeling of relaxation of viscoelastic stresses in multi-layered thin films/substrate systems due to thermal mismatch. Thin Solid Films 518, 7497 (2010).CrossRefGoogle Scholar
19.Hsueh, C.H.: Modeling of elastic deformation of multilayers due to residual stresses and external bending. J. Appl. Phys. 91, 9652 (2002).CrossRefGoogle Scholar
20.Witvrouw, A., Volkert, C.A., and Spaepen, F.: The viscosity of amorphous metallic thin films. Mater. Sci. Eng., A 134, 1274 (1991).Google Scholar
21.Loopstra, O.B., van Snek, E.R., de Keijser, T.H., and Mittemeijer, E.J.: Model for stress and volume changes of a thin film on a substrate upon annealing: Application to amorphous Mo/Si multilayers. Phys. Rev. B 44, 13519 (1991).Google Scholar
22.Hu, S.M.: Stress-related problems in silicon technology. J. Appl. Phys. (Berl.) 70, R53 (1991).Google Scholar
23.Rosenberg, S.E., Madras, C.G., Wong, P.Y., and Miaoulis, I.N.: The viscosity of germanium during substrate relaxation upon thermal anneal. J. Mater. Res. 12, 1706 (1997).Google Scholar
24.Li, C.C. and Desu, S.B.: Processing of PbTiO3 thin films. II. In situ investigation of stress relaxation. J. Vac. Sci. Technol., A 14, 7 (1996).CrossRefGoogle Scholar
25.Senez, V., Collard, D., and Baccus, B.: Analysis and application of a viscoelastic model for silicon oxidation. J. Appl. Phys. 76, 3285 (1994).Google Scholar
26.Sutardja, P. and Oldham, W.G.: Modeling of stress effects in silicon oxidation. IEEE Trans. Electron. Dev. 36, 2415 (1989).Google Scholar
27.Flugge, W.: Viscoelasticity, 2nd ed. (Springer, Berlin, Germany, 1975).Google Scholar
28.Shames, I.H. and Cozzarelli, F.A.: Elastic and Inelastic Stress Analysis (Prentice Hall, Englewood Cliffs, NJ, 1992).Google Scholar