Published online by Cambridge University Press: 07 February 2020
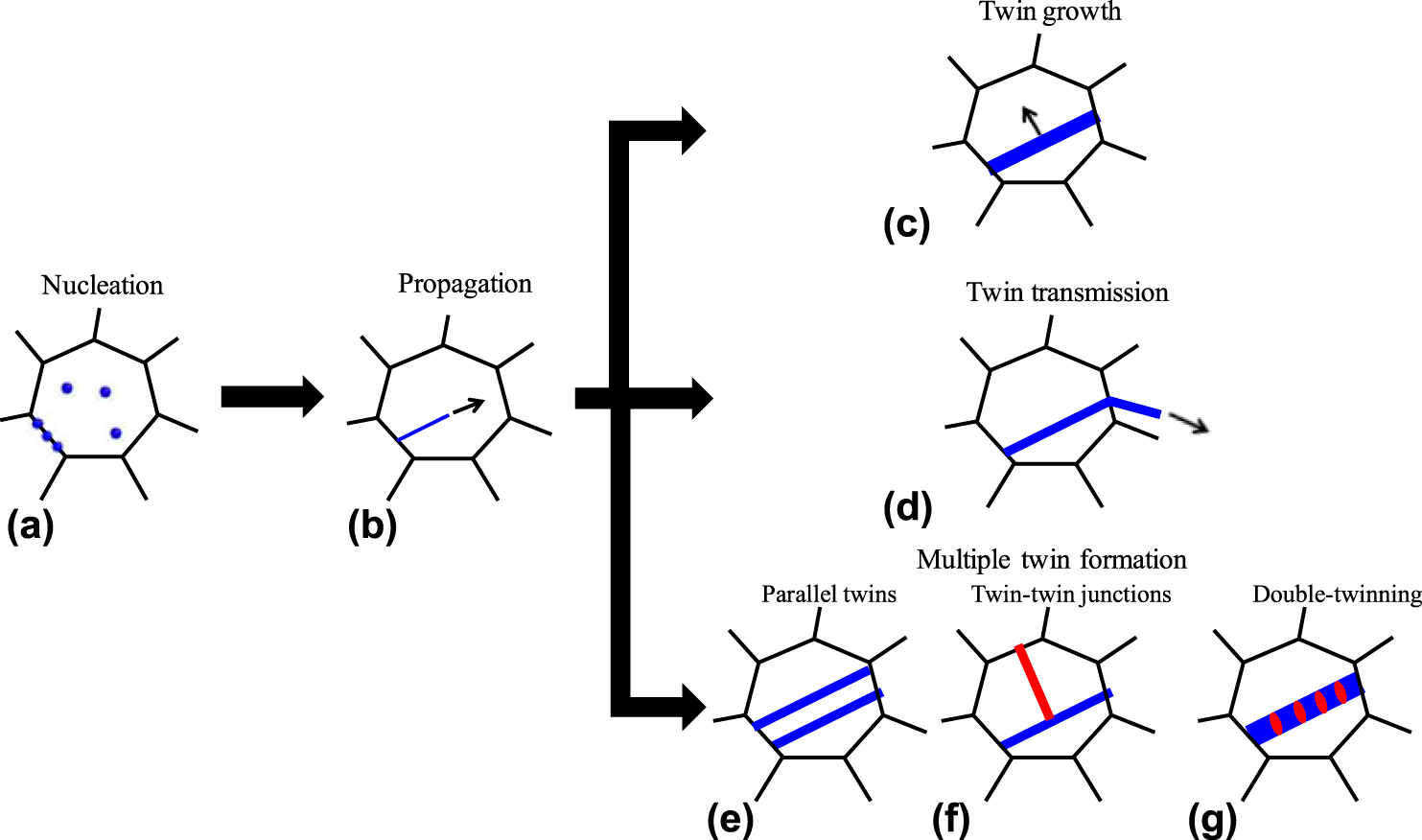
Deformation twinning is a prevalent plastic deformation mode in hexagonal close-packed (HCP) materials, such as magnesium, titanium, and zirconium, and their alloys. Experimental observations indicate that these twins occur heterogeneously across the polycrystalline microstructure during deformation. Morphological and crystallographic distribution of twins in a deformed microstructure, or the so-called twinning microstructure, significantly controls material deformation behavior, ductility, formability, and failure response. Understanding the development of the twinning microstructure at the grain scale can benefit design efforts to optimize microstructures of HCP materials for specific high-performance structural applications. This article reviews recent research efforts that aim to relate the polycrystalline microstructure with the development of its twinning microstructure through knowledge of local stress fields, specifically local stresses produced by twins and at twin/grain–boundary intersections on the formation and thickening of twins, twin transmission across grain boundaries, twin–twin junction formation, and secondary twinning.
This section of Journal of Materials Research is reserved for papers that are reviews of literature in a given area.
 $\left\{ {10\bar{1}2} \right\}$ twinning. Acta Mater. 63, 1 (2014).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ twinning. Acta Mater. 63, 1 (2014).CrossRefGoogle Scholar $\left( {10\bar{1}2} \right)$ twin during growth. Philos. Mag. 94, 2827 (2014).CrossRefGoogle Scholar
$\left( {10\bar{1}2} \right)$ twin during growth. Philos. Mag. 94, 2827 (2014).CrossRefGoogle Scholar $\left\{ {\bar{1}011} \right\}$ and
$\left\{ {\bar{1}011} \right\}$ and  $\left\{ {\bar{1}013} \right\}$ twinning dislocations at a twin boundary in hexagonal close-packed crystals. Modell. Simul. Mater. Sci. 20, 024001 (2012).CrossRefGoogle Scholar
$\left\{ {\bar{1}013} \right\}$ twinning dislocations at a twin boundary in hexagonal close-packed crystals. Modell. Simul. Mater. Sci. 20, 024001 (2012).CrossRefGoogle Scholar $\left\{ {10\bar{1}2} \right\}$ twinning in magnesium. Acta Mater. 61, 3549 (2013).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ twinning in magnesium. Acta Mater. 61, 3549 (2013).CrossRefGoogle Scholar $\left\{ {10\bar{1}2} \right\}$ twins in AZ31 magnesium alloy. Acta Mater. 100, 202 (2015).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ twins in AZ31 magnesium alloy. Acta Mater. 100, 202 (2015).CrossRefGoogle Scholar $\left\{ {\bar{1}012} \right\}$ non-cozone twin-twin interactions in magnesium. Acta Mater. 159, 65 (2018).CrossRefGoogle Scholar
$\left\{ {\bar{1}012} \right\}$ non-cozone twin-twin interactions in magnesium. Acta Mater. 159, 65 (2018).CrossRefGoogle Scholar $\left\{ {1\bar{0}11} \right\} – \left\{ {1\bar{0}12} \right\}$ double twinning in a magnesium alloy. Nat. Commun. 7, 11068 (2016).CrossRefGoogle Scholar
$\left\{ {1\bar{0}11} \right\} – \left\{ {1\bar{0}12} \right\}$ double twinning in a magnesium alloy. Nat. Commun. 7, 11068 (2016).CrossRefGoogle Scholar $\left\{ {11\bar{2}2} \right\}$ twins in titanium: A combined experimental and modelling investigation of the local state of deformation. Acta Mater. 126, 221 (2017).CrossRefGoogle Scholar
$\left\{ {11\bar{2}2} \right\}$ twins in titanium: A combined experimental and modelling investigation of the local state of deformation. Acta Mater. 126, 221 (2017).CrossRefGoogle Scholar $\left\{ {10\bar{1}2} \right\}$ extension twinning on the flow behavior of AZ31 Mg alloy. Mater. Sci. Eng., A 445, 302 (2007).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ extension twinning on the flow behavior of AZ31 Mg alloy. Mater. Sci. Eng., A 445, 302 (2007).CrossRefGoogle Scholar $\left\{ {\bar{1}012} \right\}$ twin interaction in magnesium single crystal. Mater. Res. Lett. 2, 82 (2014).CrossRefGoogle Scholar
$\left\{ {\bar{1}012} \right\}$ twin interaction in magnesium single crystal. Mater. Res. Lett. 2, 82 (2014).CrossRefGoogle Scholar $\left\langle {10\bar{1}2} \right\rangle$ twin variants sharing the same zone axis in deformed magnesium alloy. Mater. Charact. 109, 160 (2015).CrossRefGoogle Scholar
$\left\langle {10\bar{1}2} \right\rangle$ twin variants sharing the same zone axis in deformed magnesium alloy. Mater. Charact. 109, 160 (2015).CrossRefGoogle Scholar $\left\{ {11\bar{2}1} \right\}$ secondary twinning associated with
$\left\{ {11\bar{2}1} \right\}$ secondary twinning associated with  $\left\{ {11\bar{2}2} \right\}$ twin in titanium. Acta Mater. 164, 776 (2019).CrossRefGoogle Scholar
$\left\{ {11\bar{2}2} \right\}$ twin in titanium. Acta Mater. 164, 776 (2019).CrossRefGoogle Scholar $\left\{ {10\bar{1}2} \right\}$ sequential twinning in titanium. Acta Mater. 165, 547 (2019).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ sequential twinning in titanium. Acta Mater. 165, 547 (2019).CrossRefGoogle Scholar $\left\{ {11\bar{2}1} \right\} \to \left\{ {11\bar{2}2} \right\}$ double twinning in titanium. Int. J. Plast. 112, 194 (2019).CrossRefGoogle Scholar
$\left\{ {11\bar{2}1} \right\} \to \left\{ {11\bar{2}2} \right\}$ double twinning in titanium. Int. J. Plast. 112, 194 (2019).CrossRefGoogle Scholar $\left\{ {10\bar{1}2} \right\}$ twins in as-extruded pure magnesium. Scr. Mater. 69, 702 (2013).CrossRefGoogle Scholar
$\left\{ {10\bar{1}2} \right\}$ twins in as-extruded pure magnesium. Scr. Mater. 69, 702 (2013).CrossRefGoogle Scholar $\left\{ {1\bar{0}12} \right\}$ deformation twin in Mg. Nat. Commun. 10, 3308 (2019).CrossRefGoogle Scholar
$\left\{ {1\bar{0}12} \right\}$ deformation twin in Mg. Nat. Commun. 10, 3308 (2019).CrossRefGoogle Scholar