Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-11-27T00:00:28.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear free energy relationships in solid state diffusion processes

Published online by Cambridge University Press:  26 July 2012

Rajat Kapoor  and
S. T. Oyama
Rajat Kapoor
Affiliation:
Department of Chemical Engineering, Virginia Polytechnic, Blacksburg, Virginia 24061-0211
S. T. Oyama*
Affiliation:
Department of Chemical Engineering, Virginia Polytechnic, Blacksburg, Virginia 24061-0211
*
a)Author to whom correspondence should be addressed.
Get access

Abstract

This paper presents a new form of linear free energy (LFE) relationship for diffusive mass transport in oxides and other binary compounds. The relationship applies to a family of related compounds. For a given substance, i, solid-state diffusivity is related to the equilibrium constant Ki or the free energy of transformation, 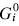, via a transfer coefficient γ, through the expression ln Di = γ ln Ki + constant 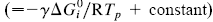. The system investigated here is the series of suboxide intermediates of vanadium pentoxide formed during temperature-programmed synthesis of vanadium nitride. The value of γ for this series is 0.27. The diffusivity values are determined by fitting a mathematical model to the experimental data. Diffusivity data are presented graphically in contour diagrams which correlate pre-exponential values, activation energies, particle sizes, and heating rates used in the temperature-programmed syntheses. An Evans–Polanyi linear relation, 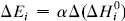, relating activation energy, Ei, to enthalpy change of transformation, 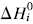, via a transfer coefficient α = 0.53, is also shown to exist for the above system. The discrepancy between α and γ is resolved by using the Horiuti concept of the stoichiometric number of the rate-determining step.

Type
Articles
Information
Journal of Materials Research , Volume 12 , Issue 2 , February 1997 , pp. 474 - 479
Copyright
Copyright © Materials Research Society 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Leffler, J. E. and Grunwald, E., Rates and Equilibria of Organic Reactions (John Wiley, New York, 1963), Chap. 6.Google Scholar
2.Brönsted, J. N. and Pedersen, K. J., Z. Phys. Chem. 108, 185 (1924).CrossRefGoogle Scholar
3.Hammett, L. P., J. Am. Chem. Soc. 59, 96 (1937); L. P. Hammett, Trans. Faraday Soc. 34, 151 (1938).CrossRefGoogle Scholar
4.Taft, R. W., J. Am. Chem. Soc. 75, 4231 (1953).CrossRefGoogle Scholar
5.Conner, W. C., Jr. and Schwarz, J. A., Chem. Eng. Commun. 55, 129 (1987).Google Scholar
6.Kraus, M., Adv. Catal. 17, 75 (1967).CrossRefGoogle Scholar
7.Evans, M. G. and Polanyi, N. P., Trans. Faraday Soc. 34, 11 (1938).CrossRefGoogle Scholar
8.Kapoor, R. and Oyama, S. T., J. Mater. Res. 12, 467 (1997).CrossRefGoogle Scholar
9.Kapoor, R. and Oyama, S. T., J. Solid State Chem. 99, 303 (1992).CrossRefGoogle Scholar
10.Oyama, S. T., Schlatter, J. C., Metcalfe, J. E., III, and Lambert, J. M., Jr., Ind. Eng. Chem. Res. 27, 1639 (1988).CrossRefGoogle Scholar
11. Standard TPR theory predicts peak temperature, Tp, to be related to heating rate, b, by the equation 2 lnT p 2 ln b = E/RT p 1 const. The value of E can be determined from the slope of a plot of 2 lnT p 2 ln b vs T 1p. The data sets here can be obtained by conducting the experiments at different heating rates. Hurst, N. W., Gentry, S. J., Jones, A., and McNicol, B. D., Catal. Rev. Sci. Eng. 24, 233 (1982).CrossRefGoogle Scholar
12.Barin, I. and Knacke, O., Thermochemical Properties of Inorganic Substances (Springer-Verlag, Berlin, 1973); D. R. Stull and H. Prophet, JANAF Thermochemical Tables (NBS, Washington, DC, 1971).Google Scholar
13.Boudart, M. and Djéga-Mariadassou, G., Kinetics of Heterogeneous Catalytic Reactions (Princeton University Press, Princeton, NJ, 1984).CrossRefGoogle Scholar
14.Horiuti, J., Ann. N.Y. Acad. Sci. 213, 5 (1973).CrossRefGoogle Scholar
15.Horiuti, J., J. Res. Inst. Catal., Hokkaido University 1, 8 (1948).Google Scholar