Article contents
High Throughput Determination of Creep Parameters Using Cantilever Bending: Part II - Primary and Steady-State through Uniaxial Equivalency
Published online by Cambridge University Press: 18 February 2020
Abstract
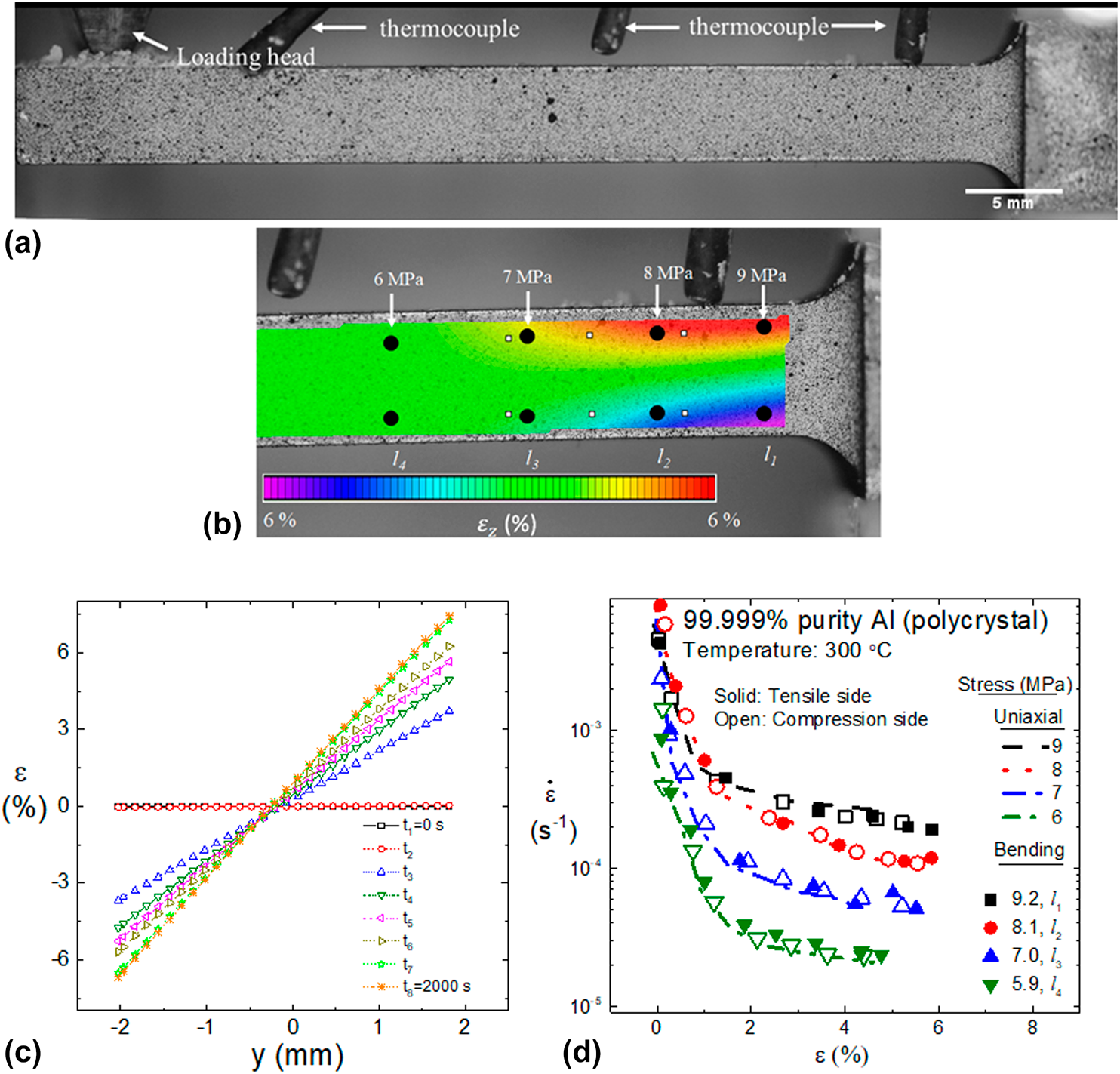
The stress and hence strain fields in a cantilever deforming as per power-law creep vary across the length and thickness of the sample, which allow obtaining multiple stress–strain pairs from a single test. Here, a high-throughput method is described to quantify the primary-cum-steady-state creep response of materials by testing a single cantilever sample in bending and mapping strain fields using digital image correlation. The method is based on the existence of stress invariant points in a cantilever, where the value of stress does not change during creep. It is demonstrated that strain evolution throughout primary and steady-state stages at these points is identical to the creep response obtained under uniaxial tests. Furthermore, the gained insights were exploited to obtain various parameters of a power-law type primary-cum-steady-state creep equation by testing only one cantilever sample. The developed method allows obtaining uniaxial creep curves at multiple stresses by testing a single cantilever, thereby reducing the time and number of samples required to understand the creep behavior of a material. The method has been validated by performing bending tests on Al and comparing the results with those of corresponding uniaxial tests.
Keywords
- Type
- Article
- Information
- Copyright
- Copyright © Materials Research Society 2020
References
- 10
- Cited by


