Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-17T21:24:18.961Z Has data issue: false hasContentIssue false
  • English
  • Français

A contribution to understanding of low-load spherical indentation—Comparison of tests on polymers and fused silica

Published online by Cambridge University Press:  13 September 2011

Jiří Nohava  and
Jaroslav Menčík
Jiří Nohava*
Affiliation:
CSM Instruments, CH-2034 Peseux, Switzerland
Jaroslav Menčík
Affiliation:
Department of Mechanics, Materials, and Machine Parts, University of Pardubice, CZ-53210 Pardubice, Czech Republic
*
a)Address all correspondence to this author. e-mail: [email protected]
Get access

Abstract

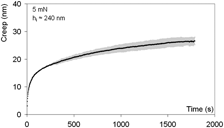
Spherical indentation, particularly at low loads, can ensure fully reversible deformations, suitable for the study of viscoelastic properties. However, there are growing concerns about the effective indenter radius in contact at small penetrations and the effect of thermal drift. The aim of this study was to characterize spherical indentation on polymethylmethacrylate (PMMA) and fused silica (FS). Several types of indentation experiments were performed on PMMA to determine its viscoelastic behavior, and a corresponding model was applied to calculate the main mechanical properties. A series of measurements on FS were performed to determine the effective indenter radius and thermal drift of the indentation system. It was shown that at low depths the effective radius of the spherical indenter can substantially differ from the nominal one and calibration of the indenter might be necessary for certain experiments. The effect of thermal drift and its consequences on creep measurements were discussed.

Keywords

NanoindentationViscoelasticityPolymer
Type
Articles
Information
Journal of Materials Research , Volume 27 , Issue 1: Focus Issue: Instrumented Indentation , 14 January 2012 , pp. 239 - 244
Copyright
Copyright © Materials Research Society 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

1.Field, J.S. and Swain, M.V.: A simple predictive model for spherical indentation. J. Mater. Res. 8, 297 (1993).CrossRefGoogle Scholar
2.Swain, M.V. and Mencik, J.: Mechanical property characterization of thin films using spherical tipped indenters. Thin Solid Films 253, 204 (1994).CrossRefGoogle Scholar
3.Bell, T.J., Bendelli, A., Field, J.S., Swain, M.V., and Thwaite, E.G.: The determination of surface plastic and elastic properties by ultra micro-indentation. Metrologia 28, 463 (1992).CrossRefGoogle Scholar
4.Oyen, M.L.: Sensitivity of polymer nanoindentation creep measurements to experimental variables. Acta Mater. 55, 3633 (2007).Google Scholar
5.Oyen, M.L. and Cook, R.: A practical guide for analysis of nanoindentation data. J. Mech. Behav. Biomed. Mater. 2, 396 (2009).CrossRefGoogle ScholarPubMed
6.Cook, R.F. and Oyen, M.L.: Nanoindentation behavior and mechanical properties measurement of polymeric materials. Int. J. Mater. Res. 98, 370 (2007).CrossRefGoogle Scholar
7.Mencik, J., He, L.H., and Swain, M.V.: Determination of visco-elastic material parameters of biomaterials by instrumented indentation. J. Mech. Behav. Biomed. Mater. 2, 318 (2009).Google Scholar
8.Menčík, J., He, L.H., and Němeček, J.: Characterization of viscoelastic-plastic properties of solid polymers by instrumented indentation. Polym. Test. 30, 101 (2010).CrossRefGoogle Scholar
9.Schwarzer, N., Chudoba, T., and Richter, F.: Investigation of ultra thin coatings using nanoindentation. Surf. Coat. Tech. 200, 5566 (2006).CrossRefGoogle Scholar
10.Chudoba, T. and Richter, F.: Investigation of creep behaviour under load during indentation experiments and its influence on hardness and modulus results. Surf. Coat. Tech. 148, 191 (2001).Google Scholar
11.Feng, G. and Ngan, A.H.W.: Effects of creep and thermal drift on modulus measurement using depth-sensing indentation. J. Mater. Res. 17(3), 660 (2002).Google Scholar
12.Tweedie, C.A. and Van Vliet, K.J.: Contact creep compliance of viscoelastic materials via nanoindentation. J. Mater. Res. 21(6), 1576 (2006).CrossRefGoogle Scholar
13.Wang, F. and Xu, K.: An investigation of nanoindentation creep in polycrystalline Cu thin film. Mater. Lett. 58, 2345 (2004).Google Scholar
14.Nohava, J., Randall, N.X., and Conté, N.: Novel ultra nanoindentation method with extremely low thermal drift: Principle and experimental results. J. Mater. Res. 24(3), 873 (2009).Google Scholar
15.VanLandingham, M.R.: Review of Instrumented Indentation. J. Res. Nat. Inst. Stand. Technol. 108(4), 249 (2003).CrossRefGoogle ScholarPubMed
16.Oliver, W.C. and Pharr, G.M.: Measurement of hardness and elastic modulus by instrumented indentation: Advances in understanding and refinements to methodology. J. Mater. Res. 19(1), 3 (2004).Google Scholar
17.Oyen, M.L.: Analytical techniques for indentation of viscoelastic materials. Philos. Mag. 86(33-35), 5625 (2006).CrossRefGoogle Scholar
18.Eswar Prasad, K., Keryvin, V., and Ramamurty, U.: Pressure sensitive flow and constraint factor in amorphous materials below glass transition. J. Mater. Res. 24(3), 890 (2009).CrossRefGoogle Scholar
19.Proctor, B.A., Whitney, I., and Johnson, J.W.: The strength of fused silica. Proc. R. Soc. London, Ser. A 297(1451), 534 (1967).Google Scholar
20.Tabor, D.: The Hardness of Metals (Clarendon Press, Oxford, England, 1951) 192 p.Google Scholar
21.Kang, B.S-J., Yao, Z., and Barbero, E.J.: Post-yielding stress-strain determination using spherical indentation. Mech. Adv. Mater. Struct. 13, 129 (2006).CrossRefGoogle Scholar
22.Herbert, E.G., Pharr, G.M., Oliver, W.C., Lucas, B.N., and Hay, J.L.: On the measurement of stress-strain curves by spherical indentation. Thin Solid Films 398–399, 331 (2001).Google Scholar
23.Bell, T.J., Field, J.S., and Swain, M.V.: Stress-strain behaviour of thin films using a spherical tipped indenter, in Thin Films: Stresses and Mechanical Properties III, edited by Nix, W.D., Bravman, J.C., Arzt, E., and Freund, L.B. (Mater. Res. Soc. Symp. Proc., Vol. 239, Pittsburgh, PA, 1992), p. 331.Google Scholar