Research Article
Dualization of the Hopf algebra of secondary cohomology operations and the Adams spectral sequence
-
- Published online by Cambridge University Press:
- 19 January 2011, pp. 203-347
-
- Article
- Export citation
Bimonads and Hopf monads on categories
-
- Published online by Cambridge University Press:
- 05 February 2010, pp. 349-388
-
- Article
- Export citation
Elementary symplectic orbits and improved K1-stability
-
- Published online by Cambridge University Press:
- 10 June 2010, pp. 389-403
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
KAG volume 7 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 18 April 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
KAG volume 7 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 18 April 2011, pp. b1-b2
-
- Article
-
- You have access
- Export citation


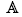 and by this we retain some of the combinatorial complexity which makes the theory so interesting. As a basic tool we use distributive laws between monads and comonads (entwinings) on
and by this we retain some of the combinatorial complexity which makes the theory so interesting. As a basic tool we use distributive laws between monads and comonads (entwinings) on 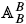 of (mixed)
of (mixed)