Combining Kasparov's generalization of a theorem of Voiculescu and Cuntz's description of KK-theory in terms of quasihomomorphisms (sections one and two), we give a simple construction of the Kasparov product (section three). This construction will be generalized in [Gre] to give a version of the product for so-called locally convex Kasparov modules over locally convex algebras in order to treat products of certain universal cycles.

We present a definition of spectral flow for any norm closed ideal J in any von Neumann algebra N. Given a path of selfadjoint operators in N which are invertible in N/J, the spectral flow produces a class in Ko(J).

Given a semifinite spectral triple (A, H, D) relative to (N, τ) with A separable, we construct a class [D] ∈ KK1(A, K(N)). For a unitary u ∈ A, the von Neumann spectral flow between D and u*Du is equal to the Kasparov product [u]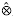A[D], and is simply related to the numerical spectral flow, and a refined C*-spectral flow.

Suppose that B is a G-Banach algebra over = ℝ or ℂ X is a finite dimensional compact metric space, ζ : P → X is a standard principal G-bundle, and Aζ = Γ(X,P ×GB) is the associated algebra of sections. We produce a spectral sequence which converges to π*(GLoAζ) with

A related spectral sequence converging to K*+1(Aζ) (the real or complex topological K-theory) allows us to conclude that if B is Bott-stable, (i.e., if π*(GLoB) → K*+1(B) is an isomorphism for all * > 0) then so is Aζ.

For a 2-category 2C we associate a notion of a principal 2C-bundle. For the 2-category of 2-vector spaces, in the sense of M.M. Kapranov and V.A. Voevodsky, this gives the 2-vector bundles of N.A. Baas, B.I. Dundas and J. Rognes. Our main result says that the geometric nerve of a good 2-category is a classifying space for the associated principal 2-bundles. In the process of proving this we develop powerful machinery which may be useful in further studies of 2-categorical topology. As a corollary we get a new proof of the classification of principal bundles. Another 2-category of 2-vector spaces has been proposed by J.C. Baez and A.S. Crans. A calculation using our main theorem shows that in this case the theory of principal 2-bundles splits, up to concordance, as two copies of ordinary vector bundle theory. When 2C is a cobordism type 2-category we get a new notion of cobordism-bundles which turns out to be classified by the Madsen–Weiss spaces.

We prove that the embedding of the derived category of 1-motives up to isogeny into the triangulated category of effective Voevodsky motives, as well as its left adjoint functor LAlbℚ, commute with the Hodge realization. This result yields a new proof of the rational form of Deligne's conjecture on 1-motives.

Lurie's representability theorem gives necessary and sufficient conditions for a functor to be an almost finitely presented derived geometric stack. We establish several variants of Lurie's theorem, making the hypotheses easier to verify for many applications. Provided a derived analogue of Schlessinger's condition holds, the theorem reduces to verifying conditions on the underived part and on cohomology groups. Another simplification is that functors need only be defined on nilpotent extensions of discrete rings. Finally, there is a pre-representability theorem, which can be applied to associate explicit geometric stacks to dg-manifolds and related objects.