Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-25T11:31:24.383Z Has data issue: false hasContentIssue false
  • English
  • Français

On K2 of varieties over number fields

Published online by Cambridge University Press:  07 January 2008

Cristian D. González-Avilés
Cristian D. González-Avilés
Affiliation:
[email protected] de Matemáticas, Universidad Andrés Bello, Chile
Get access

Abstract

Let k be a number field and let X be a smooth, projective and geometrically integral k-variety. We show that, if the geometric Néron-Severi group of X is torsion-free, then the Galois cohomology group 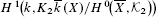is finite. Previously this group was only known to have a finite exponent. We also obtain a vanishing theorem for this group, showing in particular that it is trivial if X belongs to a certain class of abelian varieties with complex multiplication. The interest in the above cohomology group stems from its connection to the torsion subgroup of the Chow group CH2(X) of codimension 2 cycles on X. In the last section of the paper we record certain results on curves which must be familiar to all specialists in this area but which we have not formerly seen in print.

Keywords

K2Hasse principlecurves
Type
Research Article
Information
Journal of K-Theory , Volume 1 , Issue 1 , February 2008 , pp. 175 - 183
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.S., BlochK-theory and classfield theory for arithmetical surfaces. Ann. of Math. 114, no. 1, pp. 229–265 (1981)Google Scholar
2.Colliot-Thélèene, J.-L.Hilbert's Theorem 90 for K2, with application to the Chow groups of rational surfaces. Invent. Math. 71, pp. 1–20 (1983)CrossRefGoogle Scholar
3.Colliot-Thélène, J.-L. Cycles algébriques de torsion et K-théorie algébrique. In: Lecture notes in Math. 1553, pp. 1–49, Springer, New York, 1991Google Scholar
4.Colliot-Thélène, J.-L. and Raskind, W.κ2-Cohomology and the second Chow group. Math. Ann. 270, pp. 165–199 (1985)CrossRefGoogle Scholar
5.Colliot-Thélène, J.-L. and Raskind, W.Groupe de Chow de codimension deux des variétés définies sur un corps de nombres: un théorème de finitude pour la torsion. Invent. Math. 105, pp. 221–245 (1991)CrossRefGoogle Scholar
6.Coombes, K.The arithmetic of zero-cycles on surfaces with geometric genus and irregularity zero. Math. Ann. 291 pp. 429–452 (1991)CrossRefGoogle Scholar
7.Jannsen, U. Principe de Hasse cohomologique. In: Séminaire de Théorie des Nombres, Paris, 1989–1990 (David, S. Ed.), pp. 121–140. Birkhäuser, Boston, 1992Google Scholar
8.Jannsen, U. On the l-adic cohomology of varieties over number fields and its Galois cohomology. In: Galois groups over ℚ (Ihara, Y., Ribet, K. and Serre, J.P., eds.), Math. Sci. Res. Inst. Publ. 16, Springer, Berlin, 1989, pp. 315–360CrossRefGoogle Scholar
9.Kato, K. and Saito, S.Unramified class field theory of arithmetical surfaces. Ann. of Math. 118, pp. 241–275 (1983)CrossRefGoogle Scholar
10.Milne, J. Abelian varieties. In: Arithmetic Geometry, Cornell, G. and Silverman, J., Eds. Springer-Verlag 1986, pp. 103–166Google Scholar
11.Raskind, W.On K 1 of curves over global fields. Math. Ann. 288, pp. 179–193 (1990)Google Scholar
12.Serre, J.-P. and Tate, J.Good reduction of abelian varieties. Ann. of Math. 88, pp. 492–517 (1968)CrossRefGoogle Scholar
13.Suslin, A.A.Torsion in K 2 of fields. K-theory 1, pp. 5–29 (1987)Google Scholar