Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-05T04:45:27.819Z Has data issue: false hasContentIssue false
  • English
  • Français

On a local to global principle in étale K-groups of curves

Published online by Cambridge University Press:  17 May 2013

Grzegorz Banaszak  and
Piotr Krasoń
Grzegorz Banaszak
Affiliation:
Department of Mathematics and Computer Science, Adam Mickiewicz University, Poznań, [email protected]
Piotr Krasoń
Affiliation:
Department of Mathematics and Physics, Szczecin University, 70-415 Szczecin, [email protected]
Get access

Abstract

Let X be a smooth, proper and geometrically irreducible curve X defined over a number field F and let χ be a regular and proper model of X over OF,Sl. In this paper we address the problem of detecting the linear dependence over ℤl of elements in the étale K-theory of χ. To be more specific, let P ∊ Ket2n(χ) and let ⋀̂ ⊂ Ket2n(χ) be a ℤl-submodule. Let rυ: Ket2n(χ) → Ket2n(χυ) be the reduction map for υ ∉ Sl. We prove, under some conditions on X, that if rυ(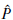) ∈ rυ (⋀̂) for almost all υ of 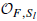then 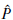∈ ⋀̂ + Ket2n(χ)tor.

Keywords

étale K-theoryalgebraic curveJacobian varietythe reduction mapPrimary 19FxxSecondary 11Gxx
Type
Research Article
Information
Journal of K-Theory , Volume 12 , Issue 1: Nanjing Special Issue on K-theory, number theory and geometry , August 2013 , pp. 183 - 201
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Banaszak, G., Gajda, W., and Krasoń, P., On Galois cohomology of some p-adic representations and étale K-theory of curves, Contemporary Math. AMS 241 (1999), 23–44Google Scholar
2.Banaszak, G., Gajda, W., Krasoń, P., On reduction map for étale K-theory of curves, Homology, Homotopy and Applications 7 (3), Proceedings of Victor's Snaith 60-th Birthday Conference, (2005), 1–10Google Scholar
3.Banaszak, G., Gajda, W., Krasoń, P. , Support problem for the intermediate Jacobians of l-adic representations, Journal of Number Theory 100 (1) (2003), 133–168Google Scholar
4.Banaszak, G., Gajda, W., Krasoń, P. , Detecting linear dependence by reduction maps, Journal of Number Theory 115 (2) (2005), 322–342CrossRefGoogle Scholar
5.Banaszak, G. and Krasoń, P. , On arithmetic in Mordell-Weil groups, Acta Arithmetica 150 (4) (2011), 315–337Google Scholar
6.Barańczuk, S., On reduction maps and support problem in K-theory and abelian varieties, Journal of Number Theory 119 (2006), 1–17CrossRefGoogle Scholar
7.Barańczuk, S. and Górnisiewicz, K., On reduction maps for the étale and Quillen K-theory of curves and applications, Jour. of K-Theory 2 (2008), 103–122CrossRefGoogle Scholar
8.Bogomolov, F.A.Sur l’algébricité des représentations l-adiques, C.R. Acad. Sci. Paris Sér. A-B 290 (1980), A701–A703Google Scholar
9.Dwyer, W., Friedlander, E., Algebraic and étale K-theory, Trans. Amer. Math. Soc. 292 (1985), 247-280Google Scholar
10.Gajda, W., GóRnisiewicz, K., Linear dependence in Mordell-Weil groups, Journal für die reine und angew. Math. 630 (2009), 219–233Google Scholar
11.Jannsen, U., Continuous étale cohomology, Math. Ann. 280 (1988), 207–245CrossRefGoogle Scholar
12.Jossen, P., Detecting linear dependence on a simple abelian variety, Commentarii Mathematici Helvetici (to appear)Google Scholar
13.Milne, J.S., Étale Cohomology, Princeton University Press, 1980Google Scholar
14.Milne, J.S., Jacobian varieties, in Arithmetic Geometry, Springer-Verlag, 1986, p. 167–212Google Scholar
15.Perucca, A., On the problem of detecting linear dependence for products of abelian varieties and tori, Acta Arithmetica 142 (2) (2010), 119–128Google Scholar
16.Reiner, I., Maximal orders, Academic Press, London, New York, San Francisco, 1975Google Scholar
17.Schinzel, A., On power residues and exponential congruences, Acta Arithmetica 27 (1975), 397–420CrossRefGoogle Scholar
18.Soulé, C., K-théorie des anneaux d'entiers de corps de nombres et cohomologie étale, Invent. Math. 55 (1979), 251–295Google Scholar
19.Weston, T., Kummer theory of abelian varieties and reductions of Mordell-Weil groups, Acta Arithmetica 110 (2003), 77–88Google Scholar