Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T20:38:19.317Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular Invariants and Twisted Equivariant K-theory II: Dynkin diagram symmetries

Published online by Cambridge University Press:  26 June 2013

David E. Evans  and
Terry Gannon
Get access

Abstract

The most basic structure of chiral conformal field theory (CFT) is the Verlinde ring. Freed-Hopkins-Teleman have expressed the Verlinde ring for the CFT's associated to loop groups, as twisted equivariant K-theory. We build on their work to express K-theoretically the structures of full CFT. In particular, the modular invariant partition functions (which essentially parametrise the possible full CFTs) have a rich interpretation within von Neumann algebras (subfactors), which has led to the developments of structures of full CFT such as the full system (fusion ring of defect lines), nimrep (cylindrical partition function), alpha-induction etc. Modular categorical interpretations for these have followed. For the generic families of modular invariants (i.e. those associated to Dynkin diagram symmetries), we provide a K-theoretic framework for these other CFT structures, and show how they relate to D-brane charges and charge-groups. We also study conformal embeddings and the 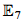modular invariant of SU(2), as well as some families of finite group doubles. This new K-theoretic framework allows us to simplify and extend the less transparent, more ad hoc descriptions of these structures obtained previously within CFT.

Keywords

twisted equivariant K-theoryconformal field theorymodular invariantsubfactor46L8046M2019K9981T40
Type
Research Article
Information
Journal of K-Theory , Volume 12 , Issue 2 , October 2013 , pp. 273 - 330
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Atiyah, M. F., Segal, G.: Twisted K-theory. Ukr. Mat. Visn. 1 (2004), 287–330; translation in Ukr. Math. Bull. 1 (2004), 291–334.Google Scholar
2.Bantay, P.: Permutation orbifolds and their applications. In: Vertex Operator Algebras in Mathematics and Physics. Proceedings, Toronto 2000. Fields Institute Communications 39. Providence: American Mathematical Society, 2003, pp. 13–23.Google Scholar
3.Beltaos, E.: Fixed points and fusion rings. JHEP to appear, arXiv:1111.3099Google Scholar
4.Birke, L., Fuchs, J., Schweigert, C.: Symmetry breaking boundary conditions and WZW orbifolds. Adv. Theor. Math. Phys. 3 (1999), 671–726.Google Scholar
5.Böckenhauer, J., Evans, D. E.: Modular invariants, graphs and alpha-induction for nets of subfactors. I. Commun. Math. Phys. 197 (1998), 361–386.; II. Commun. Math. Phys. 200 (1999), 57–103.; III. Commun. Math. Phys. 205 (1999), 183–228.Google Scholar
6.Böckenhauer, J., Evans, D. E.: Modular invariants from subfactors: Type I coupling matrices and intermediate subfactors. Commun. Math. Phys. 213 (2000), 267–289.Google Scholar
7.Böckenhauer, J., Evans, D. E.: Modular invariants from subfactors. In: Coquereaux, R., Garcia, A., Trinchero, R. (eds.) Quantum symmetries in theoretical physics and mathematics. Proceedings, Bariloche 2000. Contemp. Math. 294. Providence: American Mathematical Society, 2002, pp. 95–131.Google Scholar
8.Böckenhauer, J., Evans, D. E.: Modular invariants and subfactors. In: Longo, R. (ed.) Mathematical physics in mathematics and physics. Quantum and operator algebraic aspects. Proceedings, Siena 2000. Providence: American Mathematical Society. Fields Inst. Commun. 30 (2001), 11–37.Google Scholar
9.Böckenhauer, J., Evans, D. E., Kawahigashi, Y.: On a-induction, chiral generators and modular invariants for subfactors. Commun. Math. Phys. 208 (1999), 429–487.Google Scholar
10.Böckenhauer, J., Evans, D. E., Kawahigashi, Y.: Chiral structure of modular invariants for subfactors. Commun. Math. Phys. 210 (2000), 733–784.Google Scholar
11.Bouwknegt, P., Dawson, P., Ridout, D.: D-branes on group manifolds and fusion rings. J. High Energy Phys. 12 (2002), 065.Google Scholar
12.Braun, V., Schäfer-Nameki, S.: Supersymmetric WZW models and twisted K-theory of SO(3). Adv. Theor. Math. Phys. 12 (2008), 217–242.; hep-th/0403287.CrossRefGoogle Scholar
13.Braun, V.: Twisted K-theory of Lie groups. J. High Energy Phys. 03, 029 (2004).Google Scholar
14.Brodzki, J., Mathai, V., Rosenberg, J., Szabo, R. J.: D-Branes, RR-Fields and duality on noncommutative manifolds. Commun. Math. Phys. 277 (2008), 643–706.Google Scholar
15.Brown, K. S.: Cohomology of groups. Graduate Texts in Mathematics 87. Springer-Verlag, New York, 1994.Google Scholar
16.Cappelli, A., Itzykson, C., Zuber, J.-B.: The A-D-E classification of minimal and A 1(1) conformal invariant theories. Commun. Math. Phys. 113 (1987), 1–26.Google Scholar
17.Coste, A., Gannon, T., Ruelle, P.: Finite group modular data. Nucl. Phys. B581 (2000), 679–717.Google Scholar
18.Dijkgraaf, R., Verlinde, E.: Modular invariance and the fusion algebras. Nucl. Phys. (Proc. Suppl.) 5B (1988), 87–97.Google Scholar
19.Douglas, C. L.: On the twisted K-homology of simple Lie groups. Topology 45 (2006), 955–988.Google Scholar
20.Douglas, C. L.: Fusion rings of loop group representations. arxiv: 0901.0391v1.Google Scholar
21.Dunbar, D. C., Joshi, K. G.: Characters for coset conformal field theories and maverick examples. Int. J. Mod. Phys. A8 (1993), 4103–4121.Google Scholar
22.Echterhoff, S., Emerson, H., Kim, H. J.: KK-theoretic duality for proper twisted actions. Math. Ann. 340 (2008), 839–873.; math/0610044.CrossRefGoogle Scholar
23.Evans, D. E.: Critical phenomena, modular invariants and operator algebras. In: Cuntz, J., Elliott, G. A., Stratila, S.et al (eds.) Operator Algebras and Mathematical Physics. Proceedings, Constanţa 2001. Bucharest: The Theta Foundation, 2003, pp. 89–113.Google Scholar
24.Evans, D. E.: Twisted K-theory and modular invariants: I Quantum doubles of finite groups. In: Bratteli, O., Neshveyev, S., Skau, C. (eds.) Operator Algebras: The Abel Symposium 2004. Berlin-Heidelberg: Springer, 2006, pp. 117–144.Google Scholar
25.Evans, D. E., Gannon, T.: Modular invariants and twisted equivariant K-theory. Commun. Number Theory Phys. 3 (2009), 209–296.Google Scholar
26.Evans, D. E., Gannon, T.: The exoticness and realisability of twisted Haagerup-Izumi modular data. Comm. Math. Phys. 307 (2011), 463–512. arXiv:1006.1326.Google Scholar
27.Evans, D. E., Kawahigashi, Y.: Quantum Symmetries on Operator Algebras. Oxford: Oxford University Press, 1998.CrossRefGoogle Scholar
28.Evans, D. E., Pinto, P. T.: Subfactor realisation of modular invariants. Commun. Math. Phys. 237 (2003), 309–363.CrossRefGoogle Scholar
29.Evans, D. E., Pugh, M.: Ocneanu cells and Boltzmann weights for the SU(3) graphs. Münster J. Math. 2 (2009), 95–142.; arXiv:0906.4307.Google Scholar
30.Evans, D. E., Pugh, M.: SU(3)-Goodman-de la Harpe-Jones subfactors and the realisation of SU(3) modular invariants. Rev. Math. Phys. 21 (2009), 877–928.; arXiv:0906.4252.Google Scholar
31.Felder, G., Gawedzki, K., Kupiainen, A.: Spectra of Wess-Zumino-Witten models with arbitrary simple groups. Commun. Math. Phys. 117 (1988), 127–158.CrossRefGoogle Scholar
32.Fredenhagen, S.: D-brane charges on SO(3). J. High Energy Phys. 11, 082 (2004); hep-th/0404017.Google Scholar
33.Freed, D. S., Hopkins, M. J., Teleman, C.: Twisted equivariant K-theory with complex coefficients. J. Topol. 1 (2008), 16–44.; math.AT/0206257.Google Scholar
34.Freed, D. S., Hopkins, M. J., Teleman, C.: Loop groups and twisted K-theory I. J. Topol. 4 (2011), 737–798.; math.AT/0711.1906.CrossRefGoogle Scholar
35.Freed, D. S., Hopkins, M. J., Teleman, C.: Loop groups and twisted K-theory II. math.AT/0511232v.2.Google Scholar
36.Freed, D. S., Hopkins, M. J., Teleman, C.: Loop groups and twisted K-theory III. Ann. of Math. (2) 174 (2011), 947–1007; math.AT/0312155 v.3.CrossRefGoogle Scholar
37.Fröhlich, J., Fuchs, J., Runkel, I., Schweigert, C.: Defect lines, dualities, and generalized orbifolds. XVIth International Congress on Mathematical Physics, 608–613, World Sci. Publ., Hackensack, NJ, 2010; arXiv: math-ph/0909.5013.Google Scholar
38.Fuchs, J.: Simple WZW currents. Commun. Math. Phys. 136 (1991), 345–356.Google Scholar
39.Fuchs, J., Schellekens, A. N., Schweigert, C.: From Dynkin diagram symmetries to fixed point structures. Commun. Math. Phys. 180 (1996), 39–97.CrossRefGoogle Scholar
40.Gaberdiel, M. R., Gannon, T.: Boundary states for WZW models. Nucl. Phys. B639 (2002), 471–501.Google Scholar
41.Gaberdiel, M. R., Gannon, T.: The charges of a twisted brane. J. High Energy Phys. 01, 018 (2004); hep-th/0311242.Google Scholar
42.Gaberdiel, M. R., Gannon, T.: D-brane charges on non-simply connected groups. J. High Energy Phys. 2004, no. 4, 030, 27 pp.Google Scholar
43.Gaberdiel, M. R., Gannon, T.: Twisted brane charges for non-simply connected groups. J. High Energy Phys. 2007, no. 1, 035, 30 pp.Google Scholar
44.Gannon, T.: Modular data: the algebraic combinatorics of rational conformal field theory. J. Alg. Combin. 22 (2005), 211–250.Google Scholar
45.Gannon, T.: Moonshine Beyond the Monster: The bridge connecting algebra, modular forms and physics, Cambridge University Press, 2006.Google Scholar
46.Gannon, T., Vasudevan, M.: Charges of exceptionally twisted branes. J. High Energy Phys. 07, 035 (2005); hep-th/0504006v4.Google Scholar
47.Gannon, T., Walton, M. A.: On the classification of diagonal coset modular invariants. Commun. Math. Phys. 173 (1995), 175–197.CrossRefGoogle Scholar
48.Gannon, T., Walton, M. A.: On fusion algebras and modular matrices. Commun. Math. Phys. 206 (1999), 1–22.Google Scholar
49.Ganter, N.: Hecke operators in equivariant elliptic cohomology and generalized Moonshine. In: Groups and Symmetries. Proceedings, Montreal 2007. CRM Proc. Lecture Notes 47. Providence: Amer. Math. Soc., 2009, pp. 173–209.CrossRefGoogle Scholar
50.Goddard, P., Kent, A., Olive, D.: Unitary representations of Virasoro and super-Virasoro algebras. Commun. Math. Phys. 103 (1986), 105–119.Google Scholar
51.Haag, R.Local Quantum Physics, Springer, Berlin, 1992.Google Scholar
52.Jeffrey, L. C., Weitsman, J.: Bohr-Sommerfeld orbits in the moduli space of flat connections and the Verlinde dimension formula. Commun. Math. Phys. 150(3) (1992), 593–630.Google Scholar
53.Jones, V. F. R.: An invariant for group actions. In: de la Harpe, P. (ed.) Algèbres d'opérateurs. Proceedings, Les Plans-sur-Bex 1978. Lecture Notes in Math. 725. Berlin: Springer, 1979, pp. 237–253.Google Scholar
54.Kac, V.G.: Infinite-dimensional Lie Algebras, 3rd edn. Cambridge: Cambridge University Press, 1990.Google Scholar
55.Karoubi, M.: Twisted K-theory, old and new. In: K-theory and noncommutative geometry. EMS Ser. Congr. Rep. Zürich: European Math. Soc. 2008, pp. 117–149.; arXiv: math.KT/0701789.Google Scholar
56.Kawahigashi, Y.: From operator algebras to superconformal field theory, J. Math. Phys. 51 (2010), 015209. arXiv:1003.2925Google Scholar
57.Longo, R., Rehren, J.-H.: Nets of subfactors, Rev. Math. Phys. 7 (1995), 567–597.Google Scholar
58.McKay, J.: Graphs, singularities, and finite groups. In: Cooperstein, B., Mason, G. (eds.) The Santa Cruz Conference on Finite Groups. Proceedings, Santa Cruz 1979. Proc. Sympos. Pure Math. 37. Providence: American Mathematical Society, 1980, pp. 183–186.Google Scholar
59.Meinrenken, E.: On the quantization of conjugacy classes. L'Enseignement Math. (2) 55 (2009), 33–75.; math.DG/0707.3963.Google Scholar
60.Moore, G.: K-theory from a physical perspective. In: Topology, Geometry and Quantum Field Theory. London Math. Soc. Lecture Note Ser. 308. Cambridge: Cambridge Univ. Press, 2004, pp. 194–234.Google Scholar
61.Mohrdieck, S., Wendt, R.: Integral conjugacy classes of compact Lie groups. Manuscripta Math. 113 (2004), 531–547.Google Scholar
62.Nahm, W.: Quasi-rational fusion products. Internat. J. Modern Phys. B8 (1994), 3693–3702.Google Scholar
63.Ocneanu, A.: Paths on Coxeter diagrams: From Platonic solids and singularities to minimal models and subfactors. (Notes recorded by Goto, S.). In: Rajarama Bhat, B.V.et al. (eds.) Lectures on Operator Theory. Providence: American Mathematical Society, 2000, pp. 243–323.Google Scholar
64.Ocneanu, A.: The classification of subgroups of quantum SU(N). In: Coquereaux, R., Garcia, A., Trinchero, R. (eds.) Quantum Symmetries in Theoretical Physics and Mathematics. Proceedings, Bariloche 2000, Contemp. Math. 294. Providence: American Mathematical Society, 2002, pp. 133–159.Google Scholar
65.Ostrik, V.: Module categories for quantum doubles of finite groups. Int. Math. Res. Notices 27 (2003), 1507-1520; math.QA/0202130.Google Scholar
66.Petkova, V. B., Zuber, J.-B.: The many faces of Ocneanu cells. Nucl. Phys. B603 (2001), 449–496.; hep-th/0101151.Google Scholar
67.Chiral, Rehren K.-H.observables and modular invariants, Comm. Math. Phys. 208 (2000), 689–712.Google Scholar
68.Schellekens, A. N., Yankielowicz, S.: Simple currents, modular invariants and fixed points. Int. J. Mod. Phys. 5A (1990), 2903–2952.Google Scholar
69.Segal, G.: Equivariant K-theory. Inst. Hautes Études Sci. Publ. Math. 34 (1968), 129–151.Google Scholar
70.Segal, G.: The definition of conformal field theory. Differential Geometric Methods in Theoretical Physics (Como, 1987) (Academic Press, Boston 1988) 165–171.Google Scholar
71.Stanciu, S.: An illustrated guide to D-branes in SU(3). hep-th/0111221.Google Scholar
72.Tu, J. L.: Twisted K-theory and Poincaré duality. Trans. Amer. Math. Soc. 361 (2009), 1269–1278; math.KT/0609556.Google Scholar
73.Tu, J. L., Xu, P.: The ring structure for equivariant twisted K-theory. J. Reine Angew. Math. 635, 97–148 (2009); math.KT/0604160.Google Scholar
74.Turaev, V.G.: Quantum Invariants of Knots and 3-manifolds. de Gruyter Studies in Mathematics 18. Berlin: Walter de Gruyter, 1994.Google Scholar
75.Verrill, R. W.: Positive energy representations of LσSU(2r) and orbifold fusions. Ph.D. thesis, U Cambridge (2002).Google Scholar
76.Verstegen, D.: Conformal embeddings, rank-level duality and exceptional modular invariants. Commun. Math. Phys. 137(3) (1991), 567–586.Google Scholar
77.Wang, W.: Equivariant K-theory, wreath products, and Heisenberg algebra. Duke Math. J. 103(1) (2000), 1–23.Google Scholar
78.Wassermann, A.: Operator algebras and conformal field theory III: fusion of positive representations of LSU(n) using bounded operators. Invent. Math. 133 (1998), 467–538.Google Scholar
79.Wassermann, A.: Subfactors and Connes fusion for twisted loop groups. arXiv:1003.2292.Google Scholar
80.Xu, F.: New braided endomorphisms from conformal inclusions. Commun. Math. Phys. 192 (1998), 349–403.Google Scholar
81.Xu, F.: Mirror extensions of local nets. Commun. Math. Phys. 270 (2007), 835–847.Google Scholar