Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Доси, Анар Адыгезал оглы
and
Dosi, Anar Adıgüzel oğlu
2009.
Некоммутативные голоморфные функции от элементов алгебры Ли и задача об абсолютном базисе.
Известия Российской академии наук. Серия математическая,
Vol. 73,
Issue. 6,
p.
77.
Dosi, Anar
2009.
Fréchet Sheaves and Taylor Spectrum for Supernilpotent Lie Algebra of Operators.
Mediterranean Journal of Mathematics,
Vol. 6,
Issue. 2,
p.
181.
Dosi, Anar A
2010.
The Taylor spectrum and transversality for a Heisenberg algebra of operators.
Sbornik: Mathematics,
Vol. 201,
Issue. 3,
p.
355.
Dosi, Anar
2010.
Formally-radical Functions in Elements of a Nilpotent Lie Algebra and Noncommutative Localizations.
Algebra Colloquium,
Vol. 17,
Issue. spec01,
p.
749.
Доси, Анар Адыгезал оглы
and
Dosi, Anar Adıgüzel oğlu
2010.
Спектр Тейлора и трансверсальность для операторной алгебры Гейзенберга.
Математический сборник,
Vol. 201,
Issue. 3,
p.
39.
Пирковский, Алексей Юльевич
and
Pirkovskii, Alexei Yulievich
2012.
Гомологические размерности и изоморфизмы Ван ден Берга для ядерных алгебр Фреше.
Известия Российской академии наук. Серия математическая,
Vol. 76,
Issue. 4,
p.
65.
Pirkovskii, Alexei Yu
2012.
Homological dimensions and Van den Bergh isomorphisms for nuclear Fréchet algebras.
Izvestiya: Mathematics,
Vol. 76,
Issue. 4,
p.
702.
Dosi, Anar
2014.
Noncommutative affine spaces and Lie-complete rings.
Comptes Rendus. Mathématique,
Vol. 353,
Issue. 2,
p.
149.
Dosi, Anar
2016.
Noncommutative Localizations of Lie-Complete Rings.
Communications in Algebra,
Vol. 44,
Issue. 11,
p.
4892.
Aristov, O.Yu.
and
Pirkovskii, A.Yu.
2020.
Open embeddings and pseudoflat epimorphisms.
Journal of Mathematical Analysis and Applications,
Vol. 485,
Issue. 2,
p.
123817.


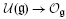 of the universal enveloping algebra
of the universal enveloping algebra 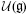 of a nilpotent Lie algebra
of a nilpotent Lie algebra 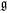 into its Arens-Michael envelope
into its Arens-Michael envelope 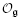 is the Taylor localization whenever
is the Taylor localization whenever 