Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-24T13:25:59.865Z Has data issue: false hasContentIssue false
  • English
  • Français

K1(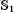) and the group of automorphisms of the algebra 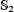of one-sided inverses of a polynomial algebra in two variables

Part of: Affine geometry Birational geometry Curves

Published online by Cambridge University Press:  24 May 2012

V.V. Bavula
V.V. Bavula*
Affiliation:
Department of Pure Mathematics, University of Sheffield, Hicks Building, Sheffield S3 7RH, UK, [email protected]
Get access

Abstract

Explicit generators are found for the group G2 of automorphisms of the algebra 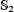of one-sided inverses of a polynomial algebra in two variables over a field. Moreover, it is proved that

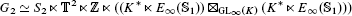
where S2 is the symmetric group, 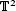is the 2-dimensional algebraic torus, E∞(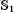) is the subgroup of GL∞(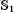) generated by the elementary matrices. In the proof, we use and prove several results on the index of an operator. The final argument is the proof of the fact that K1(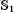) ≃ K*. The algebras 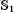and 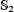are noncommutative, non-Noetherian, and not domains.

Keywords

the group of automorphismsthe inner automorphismsthe Fredholm operatorsthe index of an operatorK1(S1)the semi-direct product of groupsthe minimal primes.

MSC classification

Secondary: 14E07: Birational automorphisms, Cremona group and generalizations 14H37: Automorphisms 14R10: Affine spaces (automorphisms, embeddings, exotic structures, cancellation problem) 14R15: Jacobian problem
Type
Research Article
Information
Journal of K-Theory , Volume 10 , Issue 3 , December 2012 , pp. 583 - 601
Copyright
Copyright © ISOPP 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bavula, V. V., The Jacobian algebras, J. Pure Appl. Algebra 213 (2009), 664–685; Arxiv:math.RA/0704.3850.CrossRefGoogle Scholar
2.Bavula, V. V., The group of order preserving automorphisms of the ring of differential operators on a Laurent polynomial algebra in prime characteristic, Proc. Amer. Math. Soc. 137 (2009), 1891–1898; Arxiv:math.RA/0806.1038.Google Scholar
3.Bavula, V. V., The group of automorphisms of the first Weyl algebra in prime characteristic and the restriction map, Glasgow Math. J. 5 (2009), 263–274; Arxiv:math.RA/0708.1620.Google Scholar
4.Bavula, V. V., The algebra of one-sided inverses of a polynomial algebra, J. Pure Appl. Algebra 214 (2010), 1874–1897; Arxiv:math.RA/0903.0641.Google Scholar
5.Bavula, V. V., The group of automorphisms of the algebra of one-sided inverses of a polynomial algebra, Muenster Journal of Mathematics, to appear. ArXiv:math.AG/0903.3049.Google Scholar
6.Bavula, V. V., The group of automorphisms of the Jacobian algebra n, J. Pure Appl. Algebra, 216 (2012), 535–564; Arxiv:math.AG:0910.0999.Google Scholar
7.Bavula, V. V., The Jacobian Conjecture2n implies the Dixmier Problemn, ArXiv:math.RA/0512250.Google Scholar
8.Belov-Kanel, A. and Kontsevich, M., The Jacobian conjecture is stably equivalent to the Dixmier Conjecture, Mosc. Math. J. 7 (2) (2007), 209–218 (arXiv:math. RA/0512171).Google Scholar
9.Dixmier, J., Sur les algèbres de Weyl, Bull. Soc. Math. France 96 (1968), 209–242.CrossRefGoogle Scholar
10.Douglas, R. G., Banach Algebra Techniques in Operator Theory, Academic Press, New York, 1972.Google Scholar
11.Jacobson, N., “Structure of rings,” Am. Math. Soc. Colloq., Vol. XXXVII (rev. ed.), Am. Math. Soc., Providence, 1968.Google Scholar
12.Jung, H. W. E., Über ganze birationale Transformationen der Ebene, J. Reine Angew. Math. 184 (1942), 161–174.Google Scholar
13.Makar-Limanov, L., On automorphisms of Weyl algebra, Bull. Soc. Math. France 112 (1984), 359–363.CrossRefGoogle Scholar
14.Van der Kulk, W., On polynomial rings in two variables, Nieuw Arch. Wisk. 1(3) (1953), 33–41.Google Scholar
15.Tsuchimoto, Y., Endomorphisms of Weyl algebra and p-curvatures. Osaka J. Math. 42(2) (2005), 435–452.Google Scholar