Article contents
Hochster's theta pairing and numerical equivalence
Published online by Cambridge University Press: 28 July 2014
Abstract
Let (A, 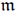 ) be a local hypersurface with an isolated singularity. We show that Hochster's theta pairing θA vanishes on elements that are numerically equivalent to zero in the Grothendieck group of A under the mild assumption that Spec A admits a resolution of singularities. This extends a result by Celikbas-Walker. We also prove that when dimA = 3, Hochster's theta pairing is positive semi-definite. These results combine to show that the counter-example of Dutta-Hochster-McLaughlin to the general vanishing of Serre's intersection multiplicity exists for any three dimensional isolated hypersurface singularity that is not a UFD and has a desingularization. We also show that, if A is three dimensional isolated hypersurface singularity that has a desingularization, the divisor class group is finitely generated torsion-free. Our method involves showing that θA gives a bivariant class for the morphism Spec (A/
) be a local hypersurface with an isolated singularity. We show that Hochster's theta pairing θA vanishes on elements that are numerically equivalent to zero in the Grothendieck group of A under the mild assumption that Spec A admits a resolution of singularities. This extends a result by Celikbas-Walker. We also prove that when dimA = 3, Hochster's theta pairing is positive semi-definite. These results combine to show that the counter-example of Dutta-Hochster-McLaughlin to the general vanishing of Serre's intersection multiplicity exists for any three dimensional isolated hypersurface singularity that is not a UFD and has a desingularization. We also show that, if A is three dimensional isolated hypersurface singularity that has a desingularization, the divisor class group is finitely generated torsion-free. Our method involves showing that θA gives a bivariant class for the morphism Spec (A/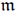 ) → Spec A.
) → Spec A.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2014
References
- 9
- Cited by


