Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-24T03:19:13.417Z Has data issue: false hasContentIssue false
  • English
  • Français

Geometry of Reidemeister classes and twisted Burnside theorem

Published online by Cambridge University Press:  04 March 2008

Alexander Fel'shtyn  and
Evgenij Troitsky
Alexander Fel'shtyn
Affiliation:
[email protected]@diamond.boisestate.eduInstytut Matematyki, Uniwersytet Szczecinski, ul. Wielkopolska 15, 70-451 Szczecin, Poland and Department of Mathematics, Boise State University, 1910 University Drive, BoiseIdaho, 83725-155, USA
Evgenij Troitsky
Affiliation:
[email protected]://mech.math.msu.su/~troitskyDept. of Mech. and Math., Moscow State University, 119992 GSP-2 Moscow, Russia
Get access

Abstract

The purpose of the present mostly expository paper (based mainly on [17, 18, 40, 16, 11]) is to present the current state of the following conjecture of A. Fel'shtyn and R. Hill [13], which is a generalization of the classical Burnside theorem.

Let G be a countable discrete group, φ one of its automorphisms, R(φ) the number of φ-conjugacy (or twisted conjugacy) classes, and S(φ) = #Fix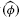 the number of φ-invariant equivalence classes of irreducible unitary representations. If one of R(φ) and S(φ) is finite, then it is equal to the other.

This conjecture plays a important role in the theory of twisted conjugacy classes (see [26], [10]) and has very important consequences in Dynamics, while its proof needs rather sophisticated results from Functional and Noncommutative Harmonic Analysis.

First we prove this conjecture for finitely generated groups of type I and discuss its applications.

After that we discuss an important example of an automorphism of a type II1 group which disproves the original formulation of the conjecture.

Then we prove a version of the conjecture for a wide class of groups, including almost polycyclic groups (in particular, finitely generated groups of polynomial growth). In this formulation the role of an appropriate dual object plays the finite-dimensional part of the unitary dual. Some counter-examples are discussed.

Then we begin a discussion of the general case (which also needs new definition of the dual object) and prove the weak twisted Burnside theorem for general countable discrete groups. For this purpose we prove a noncommutative version of Riesz-Markov-Kakutani representation theorem.

Finally we explain why the Reidemeister numbers are always infinite for Baumslag-Solitar groups.

Keywords

Reidemeister numbertwisted conjugacy classesBurnside theoremtype I grouptype II1 groupBaumslag-Solitar groupsIvanov groupOsin groupalmost polycyclic groupRiesz-Markov-Kakutani theoremDauns-Hofmann theoremFourier-Stieltjes algebra
Type
Research Article
Information
Journal of K-Theory , Volume 2 , Special Issue 3: In Memory of Yurii Petrovich Solovyev October 8, 1944–September 11, 2003 , December 2008 , pp. 463 - 506
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Arthur, J. and Clozel, L.. Simple algebras, base change, and the advanced theory of the trace formula. Princeton University Press, Princeton, NJ, 1989CrossRefGoogle Scholar
2.Barut, A. O. and Raczka, R.. Theory of group representations and applications. World Scientific Publishing Co., Singapore, second edition, 1986CrossRefGoogle Scholar
3.Connes, A.. Noncommutative geometry. Academic Press Inc., San Diego, CA, 1994Google Scholar
4.Dauns, J. and Hofmann, K. H.. Representations of rings by continuous sections, volume 83 of Mem. Amer. Math. Soc. Amer. Math. Soc., Providence, RI, 1968Google Scholar
5.de la Harpe, P.. Topics in Geometric Group Theory. Chicago Lectures in Mathematics Series. The Unversity of Chicago Press, Chicago, 2000Google Scholar
6.Dixmier, J.. C*-Algebras. North-Holland, Amsterdam, 1982Google Scholar
7.Eymard, P.. L'algèbre de Fourier d'un groupe localement compact. Bull. Soc. math. France 92 (1964): 181–236CrossRefGoogle Scholar
8.Farb, B. and Mosher, L.. On the asymptotic geometry of Abelian-by-cyclic groups. Acta Math. 184 (2) (2000): 145–202CrossRefGoogle Scholar
9.Fell, J. M. G.. The structure of algebras of operator fields. Acta Math. 106 (1961): 233–280CrossRefGoogle Scholar
10.Fel'shtyn, A.. Dynamical zeta functions, Nielsen theory and Reidemeister torsion. Mem. Amer. Math. Soc. 147 (699) (2000) :xii+146Google Scholar
11.Fel'shtyn, A. and Gonçalves, D.. Reidemeister numbers of Baumslag-Solitar groups. Eprint arXiv:math.GR/0405590, 2004. (to appear in Algebra and Discrete Mathematics)Google Scholar
12.Fel'shtyn, A. and Gonçalves, D., Twisted conjugacy classes in Sympletic groups, Mapping class groups and Braid groups (including an Appendix written with Francois Dahmani). E-print arXiv:math.GR/0708.2628Google Scholar
13.Fel'shtyn, A. and Hill, R.. The Reidemeister zeta function with applications to Nielsen theory and a connection with Reidemeister torsion. K-Theory 8 (4) (1994): 367–393CrossRefGoogle Scholar
14.Fel'shtyn, A. and Hill, R.. Dynamical zeta functions, congruences in Nielsen theory and Reidemeister torsion. In Nielsen theory and Reidemeister torsion (Warsaw, 1996), 77–116. Polish Acad. Sci., Warsaw, 1999Google Scholar
15.Fel'shtyn, A., Leonov, Y. and Troitsky, E.. Reidemister numbers of saturated weakly branch groups E-print arXiv: math.GR/0606725. Preprint MPIM 2006-79 (under revision in Geometria Dedicata)Google Scholar
16.Fel'shtyn, A. and Troitsky, E.. Twisted Burnside theorem. Preprint 46, Max-Planck-Institut für Mathematik, 2005Google Scholar
17.Fel'shtyn, A. and Troitsky, E.. A twisted Burnside theorem for countable groups and Reidemeister numbers. In Consani, K., Marcolli, M., and Manin, Yu., editors, Proc. Workshop Noncommutative Geometry and Number Theory (Bonn, 2003): 141–154. Vieweg, Braunschweig, 2006. (Preprint MPIM2004-65)CrossRefGoogle Scholar
18.Fel'shtyn, A., Troitsky, E., and Vershik, A.. Twisted Burnside theorem for type II1 groups: an example, Mathematical Research Letters 13 (5) (2006):719–728CrossRefGoogle Scholar
19.L. Fel'shtyn, A.. The Reidemeister number of any automorphism of a Gromov hyperbolic group is infinite. Zap. Nauchn. Sem. S.-Peterburg. Otdel. Mat. Inst. Steklov (POMI) 279 (2001) (6 (Geom. i Topol.)): 229–240, 250Google Scholar
20.Gonçalves, D. and Wong, P.. Twisted conjugacy classes in exponential growth groups. Bull. London Math. Soc. 35 (2) (2003): 261–268CrossRefGoogle Scholar
21.Gonçalves, Daciberg L.. The coincidence Reidemeister classes of maps on nilmanifolds. Topol. Methods Nonlinear Anal. 12 (2) (1998):375–386CrossRefGoogle Scholar
22.Gromov, Mikhael. Groups of polynomial growth and expanding maps. Inst. Hautes Études Sci. Publ. Math. 53 (1981): 53–73CrossRefGoogle Scholar
23.Grothendieck, A.. Formules de Nielsen-Wecken et de Lefschetz en géométrie algébrique. In Séminaire de Géométrie Algébrique du Bois-Marie 1965-66. SGA 5 of Lecture Notes in Math. 569: 407–441. Springer-Verlag, Berlin, 1977CrossRefGoogle Scholar
24.Hall, Ph.. A characteristic property of soluble groups. J. London Math. Soc. 12 (1937):198–200CrossRefGoogle Scholar
25.Higman, Graham, Neumann, B. H., and Neumann, Hanna. Embedding theorems for groups. J. London Math. Soc. 24 (1949):247–254CrossRefGoogle Scholar
26.Jiang, B.. Lectures on Nielsen Fixed Point Theory, of Contemp. Math. 14, Amer. Math. Soc., Providence, RI, 1983CrossRefGoogle Scholar
27.Kirillov, A. A.. Elements of the Theory of Representations. Springer-Verlag, Berlin Heidelberg New York, 1976CrossRefGoogle Scholar
28.Kurosh, A. G.. The theory of groups. Translated from the Russian and edited by Hirsch, K. A.. 2nd English ed. 2 volumes. Chelsea Publishing Co., New York, 1960Google Scholar
29.Mal'cev, A. I.. On the faithful representations of infinite groups by matrices. Mat. Sb. (NS) 8 (50) (1940):405–422 (in Russian. English translation: Amer. Math. Soc. Transl. 45 (2) (1965): 1–18)Google Scholar
30.Murphy, G. J.. C*-Algebras and Operator Theory. Academic Press, San Diego, 1990Google Scholar
31.Neumann, B. H.. Groups with finite classes of conjugate elements. Proc. London Math. Soc. 1 (3) (1951): 178–187CrossRefGoogle Scholar
32.Ol′shanskiĭ, A. Yu.. Geometry of defining relations in groups, of Mathematics and its Applications (Soviet Series) 70, Kluwer Academic Publishers Group, Dordrecht, 1991. Translated from the 1989 Russian original by Yu. A. BakhturinCrossRefGoogle Scholar
33.Osin, D.. Small cancellations over relatively hyperbolic groups and embedding theorems. Arxiv e-print math.GR/0411039, 2004Google Scholar
34.Pedersen, G. K.. C*-Algebras and Their Automorphism Groups. Academic Press, London – New York – San Francisco, 1979Google Scholar
35.Robinson, Derek J. S.. Finiteness conditions and generalized soluble groups. Part 1. Ergebnisse der Mathematik und ihrer Grenzgebiete 62, Springer-Verlag, New York, 1972Google Scholar
36.Robinson, Derek J. S.. A course in the theory of groups, of Graduate Texts in Mathematics 80, Springer-Verlag, New York, second edition, 1996Google Scholar
37.Serre, Jean-Pierre. Trees. Springer Monographs in Mathematics. Springer-Verlag, Berlin, 2003. Translated from the French original by John Stillwell, Corrected 2nd printing of the 1980 English translationGoogle Scholar
38.Shokranian, Salahoddin. The Selberg-Arthur trace formula, of Lecture Notes in Mathematics 1503, Springer-Verlag, Berlin, 1992. Based on lectures by James ArthurCrossRefGoogle Scholar
39.Thoma, E.. Über unitäre Darstellungen abzählbarer, diskreter Gruppen. Math. Ann. 153 (1964): 111–138CrossRefGoogle Scholar
40.Troitsky, E., Noncommutative Riesz theorem and weak Burnside type theorem on twisted conjugacy, Funct. Anal. Pril. 40 (2) (2006): 44–54 (in Russian), (English translation) 40 (2) (2006): 117–125 (Preprint 86 (2004) Max-Planck-Institut für Mathematik, math. OA/0606191)Google Scholar