Hostname: page-component-78c5997874-j824f Total loading time: 0 Render date: 2024-11-04T19:14:13.759Z Has data issue: false hasContentIssue false
  • English
  • Français

E-theory for C[0, 1]-algebras with finitely many singular points

Published online by Cambridge University Press:  03 March 2014

Marius Dadarlat  and
Prahlad Vaidyanathan
Get access

Abstract

We study the E-theory group E[0, 1](A, B) for a class of C*-algebras over the unit interval with finitely many singular points, called elementary C[0, 1]-algebras. We use results on E-theory over non-Hausdorff spaces to describe E[0, 1](A, B) where A is a sky-scraper algebra. Then we compute E[0, 1](A, B) for two elementary C[0, 1]-algebras in the case where the fibers A(x) and B(y) of A and B are such that E1 (A(x), B(y)) = 0 for all x, y ∈ [0, 1]. This result applies whenever the fibers satisfy the UCT, their K0-groups are free of finite rank and their K1-groups are zero. In that case we show that E[0, 1](A, B) is isomorphic to Hom(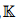0(A), 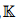0(B)), the group of morphisms of the K-theory sheaves of A and B. As an application, we give a streamlined partially new proof of a classification result due to the first author and Elliott.

Keywords

Continuous fields of C*algebrasE-theoryClassification of C*algebrasPrimary 46L35Secondary 19K3546L8046M20
Type
Research Article
Information
Journal of K-Theory , Volume 13 , Issue 2 , April 2014 , pp. 249 - 274
Copyright
Copyright © ISOPP 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bauval, Anne, R K K(X)-nucléarité (d'après G. Skandalis). K-Theory 13(1) (1998), 23–40.CrossRefGoogle Scholar
2.Dadarlat, M., Fiberwise K K-equivalence of continuous fields of C*-algebras. J. K-Theory 3(2) (2009), 205–219.Google Scholar
3.Dadarlat, M. and Elliott, G. A., One-parameter continuous fields of Kirchberg algebras. Comm. Math. Phys. 274(3) (2007), 795–819.Google Scholar
4.Dadarlat, M. and Meyer, R., E-theory for C*-algebras over topological spaces. J. Funct. Anal. 263(1) (2012), 216–247.Google Scholar
5.Dadarlat, M. and Pasnicu, C., Continuous fields of Kirchberg C*-algebras. J. Funct. Anal. 226(2) (2005), 429–451.Google Scholar
6.Dixmier, J., C* algebras 15. North Holland Publishing Company, 1977.Google Scholar
7.Kirchberg, E., Das nicht-kommutative Michael-Auswahlprinzip und die Klassifikation nicht-einfacher Algebren. In C*-algebras (Münster, 1999), pages 92–141. Springer, Berlin, 2000.Google Scholar
8.Park, E. and Trout, J.. Representable E-theory for C 0(X)-algebras. J. Funct. Anal. 177(1) (2000), 178–202.CrossRefGoogle Scholar
9.Rørdam, M. and Størmer, E.. Classification of nuclear C*-algebras. Entropy in operator algebras, Encyclopaedia of Mathematical Sciences 126. Springer-Verlag, Berlin, 2002. Operator Algebras and Non-commutative Geometry 7.Google Scholar
10.Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov's generalized K-functor. Duke Math. J. 55(2) (1987), 431–474.CrossRefGoogle Scholar