Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-03T01:00:29.275Z Has data issue: false hasContentIssue false
  • English
  • Français

Connective Algebraic K-theory

Published online by Cambridge University Press:  02 January 2014

Shouxin Dai  and
Marc Levine
Get access

Abstract

We examine the theory of connective algebraic K-theory, 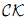, defined by taking the −1 connective cover of algebraic K-theory with respect to Voevodsky's slice tower in the motivic stable homotopy category. We extend 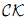to a bi-graded oriented duality theory 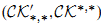when the base scheme is the spectrum of a field k of characteristic zero. The homology theory may be viewed as connective algebraic G-theory. We identify 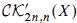for X a finite type k-scheme with the image of 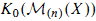in 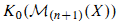, where 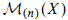is the abelian category of coherent sheaves on X with support in dimension at most n; this agrees with the (2n,n) part of the theory of connective algebraic K-theory defined by Cai. We also show that the classifying map from algebraic cobordism identifies 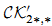with the universal oriented Borel-Moore homology theory 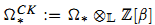having formal group law u + υ − βuυ with coefficient ring ℤ[β]. As an application, we show that every pure dimension d finite type k-scheme has a well-defined fundamental class [X]CK in ΩdCK(X), and this fundamental class is functorial with respect to pull-back for l.c.i. morphisms.

Keywords

Algebraic cobordismalgebraic K-theoryoriented homologyPrimary 14C2519E15Secondary 19E08 14F4255P42
Type
Research Article
Information
Journal of K-Theory , Volume 13 , Issue 1 , February 2014 , pp. 9 - 56
Copyright
Copyright © ISOPP 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adams, J.F., On Chern Characters and the Structure of the unitary group. Math. Proc. of the Camb. Phil. Soc. 57 (1961), 189–199.Google Scholar
2.Cai, S., Algebraic connective K-theory and the niveau filtration. J. Pure Appl. Alg. 212(7) (2008), 1695–1715.Google Scholar
3.Dai, S., Algebraic Cobordism and Grothendieck group over singular schemes, Homology, Homotopy and Appl. 12(1) (2010), 93–110.Google Scholar
4.Dundas, B. I., Levine, M., Østvær, P. A., Röndigs, O. and Voevodsky, V., Motivic homotopy theory. Lectures from the Summer School held in Nordfjordeid, 08 2002. Universitext. Springer-Verlag, Berlin, 2007.Google Scholar
5.Goerss, P. G. and Jardine, J. F., Localization theories for simplicial presheaves. Canad. J. Math. 50(5) (1998), 1048–1089.Google Scholar
6.Gutiérrez, J. J., Röndigs, O., Spitzweck, M., Østvær, P.A., Motivic slices and colored operads, Motivic slices and coloured operads. J. Topol. 5(3) (2012), 727–755.Google Scholar
7.Hirschhorn, P. S., Model categories and their localizations. Mathematical Surveys and Monographs 99. AMS, Providence, RI, 2003.Google Scholar
8.Hopkins, M., Morel, F., Slices of MGL. lecture (Hopkins), Harvard Univ. 12 2, 2004. Available as “Week 8” on a webpage of T. Lawson presenting notes from a seminar given by Hopkins, Mike, Harvard, fall of 2004. http://www.math.umn.edu/~tlawson/motivic.htmlGoogle Scholar
9.Hoyois, M., From algebraic cobordism to motivic cohomology. J. reine u. ang. Math. (online-06 2013) http://dx.doi.org/10.1515/crelle-2013-0038Google Scholar
10.Jardine, J.F., Motivic symmetric spectra, Doc. Math. 5 (2000), 445–553.Google Scholar
11.Kleiman, S., The transversality of a general translate. Composition Mathematica 28(3) (1974), 287–297.Google Scholar
12.Levine, M., Comparison of cobordism theories. J. Algebra 322(9) (2009), 3291–3317.Google Scholar
13.Levine, M., The homotopy coniveau tower. J. Topology 1 (2008), 217–267.CrossRefGoogle Scholar
14.Levine, M., Oriented cohomology, Borel-Moore homology and algebraic cobordism. Michigan Math. J. 57, Special Issue in honor of Melvin Hochster, 08 2008, 523–572.Google Scholar
15.Levine, M., Fundamental classes in algebraic cobordism. K-Theory 30(2) (2003), 129–135.Google Scholar
16.Levine, M., Techniques of localization in the theory of algebraic cycles, J. Alg. Geom. 10 (2001), 299–363.Google Scholar
17.Levine, M., Algebraic K-theory of schemes, I, preprint (2004), http://www.uni-due.de/~bm0032/publ/KthyMotI12.01.pdfGoogle Scholar
18.Levine, M. and Morel, F., Algebraic cobordism. Springer Monographs in Mathematics. Springer, Berlin, 2007.Google Scholar
19.Mocanasu, M., Borel-Moore functors and algebraic oriented theories. Preprint (2004). K-theory preprint archive 713, http://www.math.uiuc.edu/K-theory/0713/Google Scholar
20.Morel, F., An introduction to -homotopy theory. Contemporary developments in algebraic K-theory 357–441, ICTP Lect. Notes XV, Abdus Salam Int. Cent. Theoret. Phys., Trieste, 2004.Google Scholar
21.Morel, F. and Voevodsky, V., -homotopy theory of schemes, Inst. Hautes Études Sci. Publ. Math. 90 (1999), 45–143.Google Scholar
22.Panin, I., Oriented cohomology theories of algebraic varieties. II (After I. Panin and A. Smirnov). Homology, Homotopy Appl. 11(1) (2009), 349–405.Google Scholar
23.Panin, I., Pimenov, K. and Röndigs, O., On Voevodsky's algebraic K-theory spectrum. Algebraic topology, 279–330, Abel Symp. 4, Springer, Berlin, 2009.Google Scholar
24.Panin, I., Pimenov, K. and Röndigs, O., A universality theorem for Voevodsky's algebraic cobordism spectrum. Homology, Homotopy Appl. 10(2) (2008), 211–226.Google Scholar
25.Pelaez, P., On the functoriality of the slice filtration, J. K-Theory 11(1) (2013), 55–71.Google Scholar
26.Quillen, D., Higher algebraic K-theory. I. Algebraic K-theory, I: Higher K-theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pp. 85–147. Lecture Notes in Math. 341, Springer, Berlin 1973.Google Scholar
27.Röndigs, O., Spitzweck, M., Østvær, P. A., Motivic strict ring models for K-theory. Proc. Amer. Math. Soc. 138(10) (2010), 3509–3520.Google Scholar
28.Thomason, R. W. and Trobaugh, T., Higher algebraic K-theory ofschemes and of derived categories. The Grothendieck Festschrift, Vol. III, 247–435, Progr. Math. 88, Birkhäuser Boston, Boston, MA, 1990.Google Scholar
29.Voevodsky, V., On the zero slice of the sphere spectrum, Proc. Steklov Inst. Math. 246(3) (2004), 93–102.Google Scholar
30.Voevodsky, V., Open problems in the motivic stable homotopy theory. I. Motives, polylogarithms and Hodge theory, Part I (Irvine, CA, 1998), 3–34, Int. Press Lect. Ser. 3, Int. Press, Somerville, MA, 2002.Google Scholar
31.Voevodsky, V., A possible new approach to the motivic spectral sequence for algebraic K-theory. Recent progress in homotopy theory (Baltimore, MD, 2000) 371–379, Contemp. Math., 293 Amer. Math. Soc., Providence, RI, 2002.Google Scholar
32.Voevodsky, V., -homotopy theory, Proceedings of the International Congress of Mathematicians I, (Berlin, 1998). Doc. Math. 1998, Extra Vol. I, 579–604.Google Scholar
33.Weibel, C.A., Homotopy algebraic K-theory, in Algebraic K-Theory and Number Theory, Contemp. Math. 83, Amer. Math. Soc., Providence, 1989, 461–488.Google Scholar