Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bohmann, Anna Marie
and
Szymik, Markus
2024.
GENERALISATIONS OF LODAY’S ASSEMBLY MAPS FOR LAWVERE’S ALGEBRAIC THEORIES.
Journal of the Institute of Mathematics of Jussieu,
Vol. 23,
Issue. 2,
p.
811.


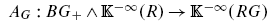 . We will complete the proof of this.
. We will complete the proof of this.