Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T03:35:41.610Z Has data issue: false hasContentIssue false
  • English
  • Français

Au-dessous de Specℤ

Published online by Cambridge University Press:  04 September 2008

Bertrand Toën  and
Michel Vaquié
Bertrand Toën
Affiliation:
Laboratoire Emile Picard, UMR CNRS 5580 Université Paul Sabatier, Toulouse, France, [email protected].
Michel Vaquié
Affiliation:
Laboratoire Emile Picard, UMR CNRS 5580 Université Paul Sabatier, Toulouse, France, [email protected].
Get access

Abstract

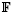In this article we use the theories of relative algebraic geometry and of homotopical algebraic geometry (cf. [HAGII]) to construct some categories of schemes defined under Specℤ. We define the categories of ℕ-schemes, 1-schemes, 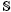-schemes, 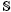+-schemes and 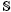1-schemes, where (from an intuitive point of view) ℕ is the semi-ring of natural numbers, 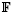1 is the field with one element, 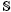is the ring spectra of integers, 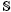+ is the semi-ring spectra of natural numbers and 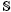1 is the ring spectra with one element. These categories of schemes are linked together by base change functors, and all of them have a base change functor to the category of ℤ-schemes. We show that the linear group Gln and the toric varieties can be defined as objects in these categories.

Keywords

Schemessymmetric monoidal categoriesGrothendieck topologieshomotopy theory
Type
Research Article
Information
Journal of K-Theory , Volume 3 , Issue 3 , June 2009 , pp. 437 - 500
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Références

Bl.Blander, B., Local projective model structure on simpicial presheaves, K-theory 24 (3) (2001), 283–301CrossRefGoogle Scholar
De.Deitmar, , Schemes over F1, dans Number fields and function fields—two parallel worlds, 87–100, Progr. Math. 239, Birkhäuser Boston, Boston, MA, 2005CrossRefGoogle Scholar
D.Deligne, P., Catégories tannakiennes, The Grothendieck Festschrift, Vol. II, 111–195, Progr. Math. 87, Birkhäuser Boston, Boston, MA, 1990Google Scholar
EKMM.Elmendorf, A.D., Kriz, I., Mandell, M.A., May, J.P., Rings, modules, and algebras in stable homotopy theory, Mathematical Surveys and Monographs 47, American Mathematical Society, Providence, RI, 1997Google Scholar
Ha.Hakim, M., Topos annelés et schémas relatifs, Ergebnisse der Mathematik und ihrer Grenzgebiete 64, Springer-Verlag Berlin-New York, 1972Google Scholar
Hol.Hollander, S., A homotopy theory for stacks, pré-publication math.AT/0110247Google Scholar
Ho.Hovey, M., Model categories, Mathematical Surveys and Monographs 63, Amer. Math. Soc., Providence 1998Google Scholar
Hu.Huettemann, T., Algebraic K-Theory of non-linear projective toric varieties, J. Pure Appl. Algebra 170 (2–3) (2002), 185–242CrossRefGoogle Scholar
Ja.Jardine, J. F., Simplicial presheaves, J. Pure and Appl. Algebra 47 (1987), 35-87CrossRefGoogle Scholar
La-Mo.Laumon, G., Moret-Bailly, L., Champs algébriques, Ergebnisse der Mathematik und ihrer Grenzgebiete 39, Springer-Verlag Berlin, 2000Google Scholar
Ma-Mo.Mac Lane, S., Moerdijk, I., Sheaves in geometry and logic. A first introduction to topos theory, Universitext. Springer-Verlag, New York, 1994Google Scholar
M-M-S-S.Mandel, M., May, P., Schwede, S., Shipley, B., Model categories of diagram spectra, Proc. London Math. Soc. (3) 82 (2001), no. 2, 441–512CrossRefGoogle Scholar
Mi.Milne, , Etale cohomology, Princeton Mathematical Series 33, Princeton University Press, Princeton, N.J., 1980Google Scholar
O.Oda, T., Convex bodies and algebraic geometry, Ergebnisse der Mathematik und ihrer Grenzgebiete 15, Springer-Verlag Berlin-New York, 1972Google Scholar
R-S-T.Richter-Gebert, J., Sturmfels, B., Theobald, T., First steps in tropical geometry, Proc. Conference on Idempotent Mathematics and Mathematical Physics, Vienna 2003 (Litvinov, G.L. and Maslov, V.P., eds.), Contemporary Mathematics, AMS.Google Scholar
Sa.Saavedra, N., Catégories Tannakiennes, Lecture Notes in Mathematics 265, Springer-Verlag, Berlin-New York, 1972Google Scholar
S.Schwede, S., Stable homotopical algebra and Γ-spaces, Math. Proc. Cambridge Philos. Soc. 126 (2) (1999), 329–356CrossRefGoogle Scholar
S-S.Schwede, S., Shipley, B., Algebras and modules in monoidal model categories, Proc. London Math. Soc. 80 (3) (2000), 491 – 511Google Scholar
So.Soulé, C., Les variétés sur le corps à un élément, Mosc. Math. J. 4 (1) (2004), 217–244CrossRefGoogle Scholar
Sp.Spitzweck, M., Operads, algebras and modules in model categories and motives, Ph.D. Thesis, Mathematisches Institüt, Friedrich-Wilhelms-Universität Bonn (2001), accessible à http://www.uni-math.gwdg.de/spitz/Google Scholar
To-Va.Toën, B., Vaquié, M., Moduli of objects in dg-categories, à parraitre aux Annales Sci. de l'ENS, pré-publication math.AG/0503269Google Scholar
HAGDAG.Toën, B., Vezzosi, G., From HAG to DAG: derived moduli stacks, in Axiomatic, enriched and motivic homotopy theory, 173–216, NATO Sci. Ser. II Math. Phys. Chem. 131, Kluwer Acad. Publ., Dordrecht, 2004CrossRefGoogle Scholar
HAGI.Toën, B., Vezzosi, G., Homotopical algebraic geometry I: Topos theory, Adv. Math. 193 (2) (2005), 257–372CrossRefGoogle Scholar
HAGII.Toën, B., Vezzosi, G., Homotopical algebraic geometry II: Geometric stacks and applications, à parraitre dans Memoires of the AMS, pré-publication math.AG/0404373Google Scholar
Ve.Vezzosi, G., A sketchy note on enriched homotopical topologies and enriched homotopical stacks, pré-publication math.CT/0507447Google Scholar