Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-03T00:20:47.810Z Has data issue: false hasContentIssue false
  • English
  • Français

Remarks on Murre's conjecture on Chow groups

Published online by Cambridge University Press:  30 October 2013

Kejian Xu  and
Ze Xu
Kejian Xu
Affiliation:
College of Mathematics, Qingdao University, Qingdao 266071, China, [email protected]
Ze Xu
Affiliation:
Institute of Mathematics, Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China, [email protected]
Get access

Abstract

For certain product varieties, Murre's conjecture on Chow groups is investigated. More precisely, let k be an algebraically closed field, X be a smooth projective variety over k and C be a smooth projective irreducible curve over k with function field K. Then we prove that if X (resp. XK) satisfies Murre's conjectures (A) and (B) for a set of Chow-Künneth projectors {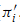, 0 ≤ i ≤ 2dim X} of X (resp. for {(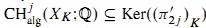)K} of XK) and if for any j, 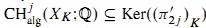, then the product variety X × C also satisfies Murre's conjectures (A) and (B). As consequences, it is proved that if C is a curve and X is an elliptic modular threefold over k (an algebraically closed field of characteristic 0) or an abelian variety of dimension 3, then Murre's conjecture (B) is true for the fourfold X × C.

Keywords

motivic decompositionChow groupcurveabelian varietyelliptic modular threefold14C25
Type
Research Article
Information
Journal of K-Theory , Volume 12 , Issue 1: Nanjing Special Issue on K-theory, number theory and geometry , August 2013 , pp. 3 - 14
Copyright
Copyright © ISOPP 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Beauville, A.. Sur l'anneau de Chow d'une variété abélienne. Math. Ann. 273(1986), 647–651Google Scholar
2.Bloch, S., Lectures on algebraic cycles, 2ed, Cambridge University Press, New York 2010Google Scholar
3.del Angel, P. L. and Müller-Stach, S.. Motives of uniruled 3-folds, Compositio Math. 112(1998), 1–16Google Scholar
4.del Angel, P. L., Müller-Stach, S.. On Chow motives of 3-folds. Trans. Amer. Math. Soc. 352(2000), 1623–1633Google Scholar
5.Deninger, C. and Murre, J. P.. Motivic decomposition of abelian schemes and the Fourier transform. J. Reine Angew. Math. 422(1991), 201–219Google Scholar
6.Fulton, W.. Intersection theory. Ergeb. Math. Grenzgeb. Springer-Verlag, Berlin, 1984Google Scholar
7.Gordon, B., Hanamura, M. and Murre, J. P.. Relative Chow-Künneth projectors for modular varieties. J. reine angew. Math. 558(2003), 1–14Google Scholar
8.Gordon, B., Hanamura, M. and Murre, J. P.. Absolute Chow-Künneth projectors for modular varieties. J. reine angew. Math. 580(2005), 139–155Google Scholar
9.Gordon, B. and Murre, J. P.. Chow motive of elliptic modular surfaces and threefolds. Math. Inst., Univ. of Leiden, Report W 96–16 (1996)Google Scholar
10.Jannsen, U.. Motivic sheaves and filtrations on Chow groups. In Proc. sympos. Pure Math. 55(1994), Part 1, 245–302Google Scholar
11.Jannsen, U.. On finite-dimensional motive and Murre's conjecture. In Algebraic cycles and motives 2, 112–142, London Math. Soc. Lecture Note Ser. 344, Cambridge Univ. Press, Cambridge, 2007Google Scholar
12.Kahn, B., Murre, J.P. and Pedrini, C., On the transcendental part of the motive of a surface. Algebraic cycles and motives 2, 143–202, London Math. Soc. Lecture Note Ser. 344, Cambridge Univ. Press, Cambridge, 2007.Google Scholar
13.Kimura, K.. Murre's conjectures for certain product varieties. J. Math. Kyoto. Univ. 47(3)(2007), 621–629Google Scholar
14.Murre, J. P.. Lectures on motives. In Transcendental Aspects of Algebraic Cycles, Proceedings of Grenoble Summer School (2001), pages 123–170, Cambridge University Press, 2004CrossRefGoogle Scholar
15.Murre, J. P.. On the motive of an algebraic surface. J. Reine und angew. Math. 409(1990), 190–204Google Scholar
16.Murre, J. P.. On a conjectural filtration on the Chow groups of an algebraic variety, I. The general conjectures and some examples. Indag. Math. N. S. 4(2)(1993), 189–201Google Scholar
17.Murre, J. P.. On a conjectural filtration on the Chow groups of an algebraic variety, II. Verification of the conjectures for threefolds which are the product on a surface and a curve. Indag. Math. N. S. 4(2)(1993), 189–201Google Scholar
18.Shermenev, A. M.. The motive of an abelian variety. Funct. Anal. 8(1974), 47–53CrossRefGoogle Scholar
19.Scholl, A. J.. Classical motives, In Proceedings of Symposia in Pure Mathematics, 55(1994), Part I, 163–187Google Scholar
20.Vial, C.. Niveau and coniveau filtrations on cohomology groups and Chow groups, Proc. LMS, 105(5)(2012), 1–35Google Scholar