Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-20T04:00:40.580Z Has data issue: false hasContentIssue false
  • English
  • Français

On the K-theory of boundary C*-algebras of Ã2 groups

Published online by Cambridge University Press:  21 June 2011

Oliver King  and
Guyan Robertson
Oliver King
Affiliation:
School of Mathematics and Statistics, University of Newcastle, NE1 7RU, [email protected]
Guyan Robertson
Affiliation:
School of Mathematics and Statistics, University of Newcastle, NE1 7RU, [email protected]
Get access

Abstract

Let Γ be an Ã2 subgroup of PGL3(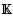), where 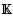is a local field with residue field of order q. The module of coinvariants C(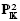,ℤ)Γ is shown to be finite, where 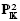is the projective plane over 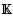. If the group Γ is of Tits type and if q ≢ 1 (mod 3) then the exact value of the order of the class [1]K0 in the K-theory of the (full) crossed product C*-algebra C(Ω) ⋊ Γ is determined, where Ω is the Furstenberg boundary of PGL3(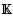). For groups of Tits type, this verifies a conjecture of G. Robertson and T. Steger.

Keywords

affine buildingboundaryoperator algebra
Type
Research Article
Information
Journal of K-Theory , Volume 9 , Issue 3 , June 2012 , pp. 521 - 536
Copyright
Copyright © ISOPP 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abramenko, P. and Brown, K., Buildings. Theory and applications, Graduate Texts in Mathematics 248. Springer, New York, 2008.Google Scholar
2.Bekka, B., de la Harpe, P. and Valette, A., Kazhdan's Property (T), Cambridge University Press, Cambridge, 2008.CrossRefGoogle Scholar
3.Cartwright, D. I., Młotkowski, W. and Steger, T., Property (T) and Ã2 groups, Ann. Inst. Fourier 44 (1993), 213–248.Google Scholar
4.Cartwright, D. I., Mantero, A. M., Steger, T. and Zappa, A., Groups acting simply transitively on the vertices of a building of type Ã2, I and II, Geom. Ded. 47 (1993), 143–166 and 167–223.CrossRefGoogle Scholar
5.Emerson, H. and Meyer, R., Euler characteristics and Gysin sequences for group actions on boundaries, Math. Ann. 334 (2006), 853–904.CrossRefGoogle Scholar
6.Robertson, G. and Steger, T., C*-algebras arising from group actions on the boundary of a triangle building, Proc. London Math. Soc. 72 (1996), 613–637.CrossRefGoogle Scholar
7.Robertson, G. and Steger, T., Affine buildings, tiling systems and higher rank Cuntz-Krieger algebras, J. reine angew. Math. 513 (1999), 115–144.CrossRefGoogle Scholar
8.Robertson, G. and Steger, T., Asymptotic K-theory for groups acting on Ã2 buildings, Canad. J. Math. 53 (2001), 809–833.CrossRefGoogle Scholar
9.Ronan, M., Lectures on Buildings, University of Chicago Press, 2009.Google Scholar
10.Singer, J., A theorem in finite projective geometry and some applications, Trans. Amer. Math. Soc. 43 (1938), 377–385.Google Scholar
11.Weiss, R., The Structure of Affine Buildings, Annals of Mathematics Studies 168, Princeton, 2009.Google Scholar
12.Zuk, A., La propriété (T) de Kazhdan pour les groupes agissant sur les polyèdres, C. R. Acad. Sci. Paris Sér. I Math. 323 (1996), 453–458.Google Scholar