Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-26T22:09:37.011Z Has data issue: false hasContentIssue false
  • English
  • Français

On the algebraic K-theory of formal power series

Published online by Cambridge University Press:  04 April 2012

Ayelet Lindenstrauss  and
Randy McCarthy
Ayelet Lindenstrauss
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, U.S.A., [email protected]
Randy McCarthy
Affiliation:
Department of Mathematics, University of Illinois at Urbana-Champaign, Urbana, IL 61801, U.S.A., [email protected]
Get access

Abstract

In this paper we extend the computation of the the typical curves of algebraic K-theory done by Lars Hesselholt and Ib Madsen to general tensor algebras. The models used allow us to determine the stages of the Taylor tower of algebraic K-theory as a functor of augmented algebras, as defined by Tom Goodwillie, when evaluated on derived tensor algebras.

For R a discrete ring, and M a simplicial R-bimodule, we let 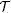R(M) denote the (derived) tensor algebra of M over R, and 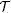πR denote the ring of formal (derived) power series in M over R. We define a natural transformation of functors of simplicial R-bimodules Φ: 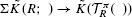which is closely related to Waldhausen's equivalence 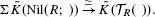We show that Φ induces an equivalence on any finite stage of Goodwillie's Taylor towers of the functors at any simplicial bimodule. This is used to show that there is an equivalence of functors 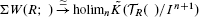, and for connected bimodules, also an equivalence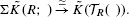

Keywords

Algebraic K-theoryK-theory of EndomorphismsGoodwillie CalculusFormal Power SeriesTensor Algebra
Type
Research Article
Information
Journal of K-Theory , Volume 10 , Issue 1 , August 2012 , pp. 165 - 189
Copyright
Copyright © ISOPP 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

B.Betley, S., Algebraic K-theory of parametrized endomorphisms, K-Theory 36 (2005), no. 3–4, 291–303.Google Scholar
BHM.Bökstedt, M., Hsiang, W.-C., Madsen, I., The cyclotomic trace and algebraic K-theory of spaces, Invent. Math. 111 (1993), no. 3, 465–539.Google Scholar
BS.Betley, S., Schlichtkrull, C., The cyclotomic trace and curves on K-theory, Topology 44 (2005), no. 4, 845–874.Google Scholar
CCGH.Carlsson, G. E., Cohen, R. L., Goodwillie, T., Hsiang, W.-C., The free loop space and the algebraic K-theory of spaces, K-Theory 1 (1987), no. 1, 53–82.Google Scholar
DGMcC.Dundas, B., Goodwillie, T., McCarthy, R., The Local structure of algebraic K-theory, preprint of book.Google Scholar
DMcC1.Dundas, B., McCarthy, R., Stable K-theory and topological Hochschild homology, Ann. of Math. 140 (1994), 685–701.Google Scholar
DMcC2.Dundas, B., McCarthy, R., Topological Hochschild homology of ring functors and exact categories, J. Pure Appl. Algebra 109 (1996), no. 3, 231–294.Google Scholar
Goodwillie, G. T., Relative algebraic K-theory and cyclic homology, Ann. of Math. (2) 124 (1986), no. 2, 347–402.Google Scholar
G2.Goodwillie, T., Calculus II, Analytic functors, K-Theory 5 (1991/1992), no. 4, 295–332.Google Scholar
G3.Goodwillie, T., Calculus III, Taylor series, Geometry and Topology 7 (2003), 645–711.CrossRefGoogle Scholar
Gr.Grayson, D., K-theory of endomorphisms, J. Algebra 48 (1977), 439–446.Google Scholar
Hesselholt, H. L., On the p-typical curves in Quillen's K-theory, Acta Math. 177 (1996), 1–53.Google Scholar
HM.Hesselholt, L., Madsen, I., On the K-theory of finite algebras over witt vectors of perfect fields, Topology 36 (1997), no. 1, 29–101.Google Scholar
Iwachita, I. Y., The Lefschetz-Reidemeister Trace in Algebraic K-theory, Ph. D. thesis, UIUC, 1999.Google Scholar
LMcC1.Lindenstrauss, A., McCarthy, R., The Taylor tower of the parametrized K-theory of endomorphisms, Geom. Topol., to appear.Google Scholar
LMcC2.Lindenstrauss, A., McCarthy, R., The algebraic K-theory of extensions of a ring by direct sums of itself, Indiana Univ. Math. J. 57 (2008), no. 2, 577–626.Google Scholar
McC.McCarthy, R., Relative algebraic K–theory and topological cyclic homology, Acta Math. 179 (1997), no. 2, 197–222.Google Scholar
Milnor, M. J., On the construction of FK, in Adams, J. F., Algebraic topology: a student's guide, London Mathematical Society Lecture Note Series 4, Cambridge University Press, London-New York, 1972.Google Scholar
NR.Neeman, A., Ranicki, A., Noncommutative localisation in algebraic K-theory. I, Geom. Topol 8 (2004), 1385–1425.Google Scholar
W1.Waldhausen, F., Algebraic K-theory of generalized free products. I, II, Ann. of Math. (2) 108 (1978), no. 1, 135–204.Google Scholar
W2.Waldhausen, F., Algebraic K-theory of spaces, in Algebraic and Geometric Topology (Rutgers 1983), 318–419, Lecture Notes in Math. 1126, Springer-Verlag, Berlin-New York, 1985.Google Scholar