Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yagita, Nobuaki
2012.
A note on the Witt group and theKO-theory of complex Grassmannians.
Journal of K-Theory,
Vol. 9,
Issue. 1,
p.
161.
YAGITA, Nobuaki
2012.
NOTE ON THE MOD p MOTIVIC COHOMOLOGY OF ALGEBRAIC GROUPS.
Kyushu Journal of Mathematics,
Vol. 66,
Issue. 2,
p.
245.
YAGITA, Nobuaki
2020.
MOTIVIC COHOMOLOGY OF TWISTED FLAG VARIETIES.
Kyushu Journal of Mathematics,
Vol. 74,
Issue. 1,
p.
43.
Yagita, Nobuaki
2024.
Étale cohomologies of quadrics over $\mathbf{R}$.
Kodai Mathematical Journal,
Vol. 47,
Issue. 2,
Benoist, Olivier
2025.
Steenrod operations and algebraic classes.
Tunisian Journal of Mathematics,
Vol. 7,
Issue. 1,
p.
53.


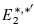 -term
-term