Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-23T14:32:35.339Z Has data issue: false hasContentIssue false
  • English
  • Français

Monodromy group for a strongly semistable principal bundle over a curve, II

Published online by Cambridge University Press:  03 January 2008

Indranil Biswas  and
A. J. Parameswaran
Indranil Biswas
Affiliation:
[email protected] of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India
A. J. Parameswaran
Affiliation:
[email protected] of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai 400005, India
Get access

Abstract

Let X be a geometrically irreducible smooth projective curve defined over a field k. Assume that X has a k–rational point; fix a k–rational point x ε X. From these data we construct an affine group scheme 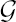X defined over the field k as well as a principal 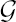X–bundle 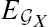over the curve X. The group scheme 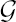X is given by a ℚ–graded neutral Tannakian category built out of all strongly semistable vector bundles over X. The principal bundle 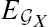is tautological. Let G be a linear algebraic group, defined over k, that does not admit any nontrivial character which is trivial on the connected component, containing the identity element, of the reduced center of G. Let EG be a strongly semistable principal G–bundle over X. We associate to EG a group scheme M defined over k, which we call the monodromy group scheme of EG, and a principal M–bundle EM over X, which we call the monodromy bundle of EG. The group scheme M is canonically a quotient of 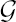X, and EM is the extension of structure group of . The group scheme M is also canonically embedded in the fiber Ad(EG)x over x of the adjoint bundle.

Keywords

Neutral Tannakian categoryprincipal bundlesemistability
Type
Research Article
Information
Journal of K-Theory , Volume 1 , Issue 3 , June 2008 , pp. 583 - 607
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Biswas, I., Parameswaran, A.J. and Subramanian, S.: Monodromy group for a strongly semistable principal bundle over a curve, Duke Math. Jour. 132 (2006), 1–48CrossRefGoogle Scholar
2.Borel, A.: Linear Algebraic Groups, Second edition. Graduate Texts in Mathematics 126. Springer-Verlag, New York, 1991Google Scholar
3.Deligne, P. and Milne, J. S.: Tannakian Categories, in: Hodge cycles, motives, and Shimura varieties (by Deligne, P., Milne, J.S., Ogus, A. and Shih, K.-Y.), pp. 101–228, Lecture Notes in Mathematics 900, Springer-Verlag, Berlin-Heidelberg-New York, 1982CrossRefGoogle Scholar
4.Harder, G.Narasimhan, M. S.: On the cohomology groups of moduli spaces of vector bundles on curves, Math. Ann. 212 (1975), 215–248CrossRefGoogle Scholar
5.Langton, S.G.: Valuative criteria for families of vector bundles on algebraic varieties, Ann. of Math. 101 (1975), 88–110CrossRefGoogle Scholar
6.Nori, M. V.: On the representations of the fundamental group scheme, Compos. Math. 33 (1976), 29–41Google Scholar
7.Nori, M. V.: The fundamental group scheme, Proc. Ind. Acad. Sci. (Math. Sci.) 91 (1982), 73–122CrossRefGoogle Scholar
8.Ramanan, S.Ramanathan, A.: Some remarks on the instability flag, Tôhoku Math. Jour. 36(1984), 269–291Google Scholar
9.Ramanathan, A.: Stable principal bundles on a compact Riemann surface, Math. Ann. 213 (1975), 129–152CrossRefGoogle Scholar
10.Saavedra Rivano, N.: Catégories Tannakiennes, Lecture Notes in Mathematics 265, Springer-Verlag, Berlin-Heidelberg-New York, 1972Google Scholar