Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-23T11:26:49.244Z Has data issue: false hasContentIssue false
  • English
  • Français

k-invariants for K-theory of curves over global fields

Published online by Cambridge University Press:  07 January 2009

Dominique Arlettaz  and
Grzegorz Banaszak
Dominique Arlettaz
Affiliation:
[email protected], Université de Lausanne, 1015 - Lausanne, Switzerland
Grzegorz Banaszak
Affiliation:
[email protected] of Mathematics and Computer Science, Adam Mickiewicz University, Poznań, Poland
Get access

Abstract

We investigate the k-invariants for the K-theory and étale K-theory spaces of schemes. We give numerical estimates of the orders of k-invariants for the K-theory and étale K-theory spaces of regular and proper models over 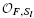of smooth, proper and geometrically irreducible curves defined over global fields F.

Keywords

k-invariantsK-theory of curvesGalois cohomology
Type
Research Article
Information
Journal of K-Theory , Volume 4 , Issue 2 , October 2009 , pp. 333 - 346
Copyright
Copyright © ISOPP 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ar.Arlettaz, D., Algebraic K-theory of rings from a topological viewpoint, Publicacions Mathemátiques 44 (2000), 3–84CrossRefGoogle Scholar
AB.Arlettaz, D., Banaszak, G., On the non-torsion elements in the algebraic K-theory of rings of integers, Journal Reine Angew. Math. 461 (1995), 63–79Google Scholar
Au.Ausoni, C., On the Hurewicz map and Postnikov invariants of Kℤ, Cohomological Methods in Homotopy Theory (Bellaterra 1998), Progress in Math. Birkhäuser, Basel 196 (2001)Google Scholar
BGK1.Banaszak, G.,Gajda, W., Krasoń, P., Support problem for the intermediate Jacobians of l-adic representations, Journal of Number Theory 100 no. 1 (2003), 133–168CrossRefGoogle Scholar
BGK2.Banaszak, G., Gajda, W., Krasoń, P., On reduction map for étale K-theory of curves, Homology, Homotopy and Applications, Proceedings of Victor Snaith's 60th Birthday Conference, 7 (3) (2005), 1–10CrossRefGoogle Scholar
BGK3.Banaszak, G., Gajda, W., and Krasoń, P., On Galois cohomology of some p-adic representations and étale K-theory of curves, Contemporary Math. AMS 241 (1999), 23–44CrossRefGoogle Scholar
Bo.Borel, A., Stable real cohomology of arithmetic groups, Ann. Sci. École Nor. Sup. 7 (4) (1974), 235–272CrossRefGoogle Scholar
D.Deligne, P., La conjecture de Weil, I, Publ. Math. IHES, 43 (1974), 273–307CrossRefGoogle Scholar
DF.Dwyer, W., Friedlander, E., Algebraic and étale K-theory, Trans. Amer. Math. Soc. 292 (1985), 247–280Google Scholar
DFST.Dwyer, W., Friedlander, E., Snaith, V., Thomason, R., Algebraic K-theory eventually surjects onto topological K-theory, Invent. Math. 66 (1982), 481–491CrossRefGoogle Scholar
FW.Friedlander, E. and Weibel, C., An overview of algebraic K-theory, Proceedings of the Workshop and Symposium: Algebraic K-Theory and Its Applications, Bass, H., Kuku, A., Pedrini, C. editors World Scientific, Singapore, New Jersey (1999), 1–119Google Scholar
H.Huebschmann, J., The homotopy type of FΨq. The complex and symplectic cases, Applications of Algebraic K-theory to Algebraic Geometry and Number Theory, Contemp. Math. 55, Part II (1986), 487–518CrossRefGoogle Scholar
J.Jannsen, U., On the l-adic cohomology of varieties over number fields and its Galois cohomology, Mathematical Science Research Institute Publications, Springer-Verlag 16 (1989), 315–360Google Scholar
Q1.Quillen, D., Higher Algebraic K-theory: I, Lecture Notes in Mathematics 341 (1973), 85–147, Springer-VerlagGoogle Scholar
Q2.Quillen, D., Finite generation of the groups Ki of rings of integers, Lecture Notes in Mathematics (1973), 179–214, Springer-VerlagGoogle Scholar
Q3.Quillen, D., On the cohomology and K-theory of the general linear groups over a finite field, Ann. of Math. 96 (2) (1972), 552–586CrossRefGoogle Scholar
Se.Serre, J.P., Abelian l-adic representations and elliptic curves, McGill University Lecture Notes, W.A. Benjamin, New York, Amsterdam (1968)Google Scholar
ST.Serre, J.P., Tate, J., Good reduction of abelian varieties and applications, Ann. of Math. 88, no 3 (1968), 492–517CrossRefGoogle Scholar
So1.Soulé, C., K-théorie des anneaux d'entiers de corps de nombres et cohomologie étale, Inv. Math. 55 (1979), 251–295CrossRefGoogle Scholar
So2.Soulé, C., Groupes de Chow et K-théorie de variétés sur un corps fini, Math. Ann. 268 (1984), 317–345CrossRefGoogle Scholar
We.Weibel, C., Introduction to algebraic K-theory, book in progress at Charles Weibel home page, http://www.math.rutgers.edu/weibel/Google Scholar
W.Whitehead, G.W., Elements of Homotopy Theory, Graduate Texts in Math. 61 (1978), Springer-VerlagGoogle Scholar