Article contents
The full orbifold K-theory of abelian symplectic quotients
Published online by Cambridge University Press: 10 June 2010
Abstract
In their 2007 paper, Jarvis, Kaufmann, and Kimura defined the full orbifoldK-theory of an orbifold 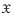 , analogous to the Chen-Ruan orbifold cohomology of
, analogous to the Chen-Ruan orbifold cohomology of 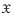 in that it uses the obstruction bundle as a quantum correction to the multiplicative structure. We give an explicit algorithm for the computation of this orbifold invariant in the case when
in that it uses the obstruction bundle as a quantum correction to the multiplicative structure. We give an explicit algorithm for the computation of this orbifold invariant in the case when 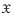 arises as an abelian symplectic quotient. To this end, we introduce the inertial K-theory associated to a T -action on a stably complex manifold M, where T is a compact abelian Lie group. Our methods are integral K-theoretic analogues of those used in the orbifold cohomology case by Goldin, Holm, and Knutson in 2005. We rely on the K-theoretic Kirwan surjectivity methods developed by Harada and Landweber. As a worked class of examples, we compute the full orbifold K-theory of weighted projective spaces that occur as a symplectic quotient of a complex affine space by a circle. Our computations hold over the integers, and in the particular case of these weighted projective spaces, we show that the associated invariant is torsion-free.
arises as an abelian symplectic quotient. To this end, we introduce the inertial K-theory associated to a T -action on a stably complex manifold M, where T is a compact abelian Lie group. Our methods are integral K-theoretic analogues of those used in the orbifold cohomology case by Goldin, Holm, and Knutson in 2005. We rely on the K-theoretic Kirwan surjectivity methods developed by Harada and Landweber. As a worked class of examples, we compute the full orbifold K-theory of weighted projective spaces that occur as a symplectic quotient of a complex affine space by a circle. Our computations hold over the integers, and in the particular case of these weighted projective spaces, we show that the associated invariant is torsion-free.
- Type
- Research Article
- Information
- Copyright
- Copyright © ISOPP 2010
References
- 1
- Cited by


