Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T03:20:52.831Z Has data issue: false hasContentIssue false
  • English
  • Français

Equivariant Intersection Theory and Surgery Theory for Manifolds with Middle Dimensional Singular Sets

Published online by Cambridge University Press:  07 March 2008

Anthony Bak  and
Masaharu Morimoto
Anthony Bak
Affiliation:
[email protected] of Mathematics, University of Bielefeld, 33615 Bielefeld, Germany
Masaharu Morimoto
Affiliation:
[email protected] School of Natural Science and Technology, Okayama University, Okayama, 700-8530, Japan
Get access

Abstract

Let G denote a finite group and n = 2k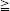 6 an even integer. Let X denote a simply connected, compact, oriented, smooth G-manifold of dimension n. Let L denote a union of connected, compact, neat submanifolds in X of dimension 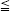k. We invoke the hypothesis that L is a G-subcomplex of a G-equivariant smooth triangulation of X and contains the singular set of the action of G on X. If the dimension of the G-singular set is also k then the ordinary equivariant self-intersection form is not well defined, although the equivariant intersection form is well defined. The first goal of the paper is to eliminate the deficiency above by constructing a new, well defined, equivariant, self-intersection form, called the generalized (or doubly parametrized) equivariant self-intersection form. Its value at a given element agrees with that of the ordinary equivariant self-intersection form when the latter value is well defined. Let 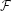denote a finite family of immersions withtrivial normal bundle of k-dimensional, connected, closed, orientable, smooth manifolds into X. Assume that the integral (and mod 2) intersection forms applied to members of 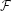and to orientable (and nonorientable) k-dimensional members of L are trivial. Then the vanishing of the equivariant intersection form on 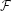× 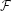and the generalized equivariant self-intersection form on 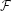is a necessary and sufficient condition that 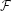is regularly homotopic to a family of disjoint embeddings, each of which is disjoint from L. This property, when 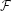is a finite family of immersions of the k-dimensional sphere Sk into X, is just what is needed for constructing an equivariant surgery theory for G-manifolds X as above whose G-singular set has dimension less than or equal to k. What is new for surgery theory is that the equivariant surgery obstruction is defined for an almost arbitrary singular set of dimension 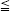k and in particular, the k-dimensional components of the singular set can be nonorientable.

Keywords

Equivariant surgerysurgery obstructionform parameterquadratic modulegroup actionfixed pointhomotopy equivalence
Type
Research Article
Information
Journal of K-Theory , Volume 2 , Special Issue 3: In Memory of Yurii Petrovich Solovyev October 8, 1944–September 11, 2003 , December 2008 , pp. 507 - 600
Copyright
Copyright © ISOPP 2008

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Anderson, G. A., Surgery with Coefficients, Springer Lecture Notes in Math. 591, Springer, Berlin-Heidelberg-New York, 1977Google Scholar
2.Bak, A., K-Theory of Forms, Ann. Math. Stud. 98, Princeton University Press, Princeton, 1981Google Scholar
3.Bak, A., Induction for finite groups revisited, J. Pure and Applied Alg. 104 (1995), 235–241CrossRefGoogle Scholar
4.Bak, A. and Morimoto, M., Equivariant surgery and applications, In: Dovermann, K. H. (Ed.), Proc. of Conf. on Topology in Hawaii 1990, pp.13–25, World Scientific, Singapore, 1992Google Scholar
5.Bak, A. and Morimoto, M., K-theoretic groups with positioning map and equivariant surgery, Proc. Japan Acad. 70 Ser. A (1994), 6–11Google Scholar
6.Bak, A. and Morimoto, M., Equivariant surgery with middle dimensional singular sets. I, Forum Math. 8 (1996), 267–302CrossRefGoogle Scholar
7.Bak, A. and Morimoto, M., The dimension of spheres with smooth one fixed point actions, Forum Math. 17 (2005), 199–216CrossRefGoogle Scholar
8.Browder, W., Surgery on Simply-Connected Manifolds, Springer, Berlin-Heidelberg-New York, 1972CrossRefGoogle Scholar
9.Cappell, S. and Weinberger, S., Replacement of fixed sets and of their normal representations in transformation groups of manifolds, In: Quinn, F. (Ed.), Prospects in Topology (Princeton, 1994), pp.67–109, Ann. Math. Stud. 138, Princeton Univ. Press, Princeton, 1995Google Scholar
10.Cappell, S. and Weinberger, S., Surgery theoretic methods in group actions, In: Cappell, S., Ranicki, A. and Rosenberg, J. (Eds.), Surveys on Surgery Theory, Vol. 2. pp.285–317, Ann. Math. Stud. 149, Princeton Univ. Press, Princeton, 2001Google Scholar
11.Cartan, H. and Eilenberg, S., Homological Algebra, Princeton University Press, Princeton, 1956Google Scholar
12.Dovermann, K. H. and Petrie, T., G-surgery II, Memoirs 37, No.260, Amer. Math. Soc., Providence, 1982Google Scholar
13.Dress, A., Induction and structure theorems for Grothendieck and Witt rings of orthogonal representations of finite groups, Bull. Amer. Math. Soc. 79 (1973), 7491–745CrossRefGoogle Scholar
14.Dress, A., Induction and structure theorems for orthogonal representations of finite groups, Ann. of Math. 102 (1975), 291–325CrossRefGoogle Scholar
15.Hirsch, M. W., Differential Topology, Springer, Berlin-Heiderberg-New York, 1976CrossRefGoogle Scholar
16.Laitinen, E. and Morimoto, M., Finite groups with smooth one fixed point actions on spheres, Forum Math. 10 (1998), 479–520CrossRefGoogle Scholar
17.Laitinen, E., Morimoto, M. and Pawałowski, K., Deleting-inserting theorem for smooth actions of finite solvable groups on spheres, Comment. Math. Helv. 70 (1995), 10–38CrossRefGoogle Scholar
18.Laitinen, E. and Pawałowski, K., Smith equivalence of representations for finite perfect groups, Proc. Amer. Math. Soc. 127 (1999), 297–307CrossRefGoogle Scholar
19.Lück, W. and Madsen, I., Equivariant L-theory I, Math. Z. 203 (1990), 503–526CrossRefGoogle Scholar
20.Lück, W. and Madsen, I., Equivariant L-theory II, Math. Z. 204 (1990), 253–268CrossRefGoogle Scholar
21.Milnor, J. W., Lectures on the h-Cobordism Theorem, Notes by Siebenmann, L. and Sondow, J., Princeton University Press, Princeton, 1965CrossRefGoogle Scholar
22.Morimoto, M., On one fixed point actions on spheres, Proc. Japan Acad. 63 Ser. A (1987), 95–97Google Scholar
23.Morimoto, M., S4 does not have one fixed point actions, Osaka J. Math. 25 (1988), 575–580Google Scholar
24.Morimoto, M., Most of the standard spheres have one fixed point actions of A5, In: Kawakubo, K. (Ed.), Transformation Groups, Lecture Notes in Math. 1375, pp.240–258, Springer, Berlin, 1989CrossRefGoogle Scholar
25.Morimoto, M., Bak groups and equivariant surgery, K-Theory 2 (1989), 465–483CrossRefGoogle Scholar
26.Morimoto, M., Bak groups and equivariant surgery. II, K-Theory 3 (1990), 505–521CrossRefGoogle Scholar
27.Morimoto, M., Most standard spheres have one fixed point actions of A5. II, K-Theory 4 (1991), 289–302CrossRefGoogle Scholar
28.Morimoto, M., Equivariant surgery theory: Deleting–inserting theorems of fixed point manifolds on spheres and disks, K-Theory 15 (1998), 13–32CrossRefGoogle Scholar
29.Morimoto, M., A geometric quadratic form of 3-dimensional normal maps, Top. and Its Appl. 83 (1998), 77–102CrossRefGoogle Scholar
30.Morimoto, M., Equivariant surgery with middle dimensional singular sets. II: Equivariant framed cobordism invariance, Trans. Amer. Math. Soc. 353 (2001), 2427–2440CrossRefGoogle Scholar
31.Morimoto, M., Induction theorems of surgery obstruction groups, Trans. Amer. Math. Soc. 355 no. 6 (2003), 2341–2384CrossRefGoogle Scholar
32.Morimoto, M. and Pawałowski, K., Smooth actions of Oliver groups on spheres, Topology 42 (2003), 395–421CrossRefGoogle Scholar
33.Morimoto, M. and Uno, K., Remarks on one fixed point A5-actions on homotopy spheres, In: Jackowski, S., Oliver, B. and Pawałowski, K. (Eds.), Algebraic Topology Poznań 1989, Lecture Notes in Math. 1478, pp.337–364, Springer, Berlin, 1991Google Scholar
34.Nakayama, T., On modules of trivial cohomology over a finite group, II, Nagoya Math. J. 12 (1957), 171–176CrossRefGoogle Scholar
35.Pawałowski, K., Smith equivalence of group modules and the Laitinen conjecture. A survey, In: Grove, K., Madsen, I. H. and Pedersen, E. K. (Eds.), Geometry and Topology: Aarhus (1998), Contemp. Math. 258, pp.343–350, Amer. Math. Soc., Providence, 2000Google Scholar
36.Pawałowski, K., Manifolds as fixed point sets of smooth compact Lie group actions, In: Bak, A., Morimoto, M. and Ushitaki, F. (Eds.), Current Trends in Transformation Goups, K-Monogr. Math. 7, pp.79–104, Kluwer Acad. Publ., Dordrecht, 2002Google Scholar
37.Pawałowski, K. and Solomon, R., Smith equivalence and finite Oliver groups with Laitinen number 0 or 1, Algebr. Geom. Topol. 2 (2002), 843–895CrossRefGoogle Scholar
38.Petrie, T., Pseudoequivalences of G manifolds, In: Proc. Symp. PureMath. 32, pp.169–210, Amer. Math. Soc., Providence, 1978Google Scholar
39.Petrie, T., One fixed point actions on spheres I, Adv. Math. 46 (1982), 3–14CrossRefGoogle Scholar
40.Petrie, T. and Randall, J. D., Transformation Groups on Manifolds, Dekker, New York, 1984Google Scholar
41.Rim, D. S., Modules over finite groups, Ann. Math. 69 (1959), 700–712CrossRefGoogle Scholar
42.Spanier, E. H., Algebraic Topology, McGraw-Hill, New York, 1966Google Scholar
43.Wall, C. T. C., Surgery on Compact Manifolds, Academic Press, London, 1970Google Scholar